Effect of Dielectric on Capacitance | Physics for JEE Main & Advanced PDF Download
What are Dielectrics?
- Dielectrics are basically insulating and non-conducting substances. They are bad conductors of electric current. Dielectrics are capable of holding electrostatic charges while emitting minimal energy. This energy is usually in the form of heat.
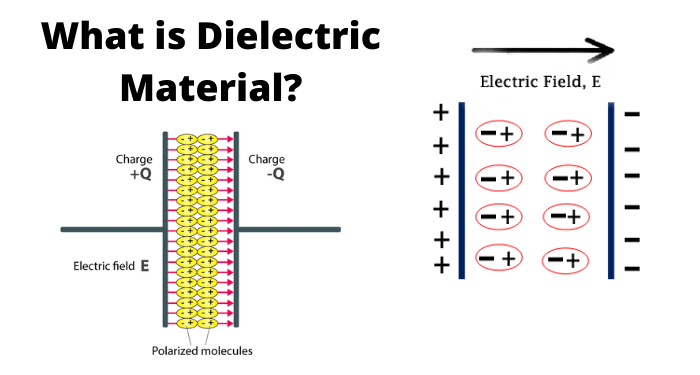
- The common examples of dielectrics include mica, plastics, porcelain, metal oxides and glass etc. It is important for you to note that dry air is also a dielectric.
What is the Dielectric Constant?
When we put a dielectric slab in between two plates of a parallel plate capacitor, the ratio of the applied electric field strength to the strength of the reduced value of electric field capacitor is called the dielectric constant. It is given as
K = Eo/E
Eo is greater than or equal to E, where Eo is the field with the slab and E is the field without it. The larger the dielectric constant, the more charge can be stored. Completely filling the space between capacitor plates with a dielectric, increases the capacitance by a factor of the dielectric constant:
C = KCo,
where Co is the capacitance with no slab between the plates. This is all about a quick recap. Now let us move ahead and see what effect dielectrics have on the capacitance.
Force Between the Plates of a Capacitor
In a capacitor as plates carry equal and opposite charges, there is a force of attraction between the plates. To calculate this force, we use the fact that the electric field is conservative and in a conservative field .
In the case of parallel plate capacitor:
[as
]
So,
The negative sign implies that the force is attractive.
Effect of Dielectric on Capacitance
We usually place dielectrics between the two plates of parallel plate capacitors. They can fully or partially occupy the region between the plates. When we place the dielectric between the two plates of a parallel plate capacitor, the electric field polarises it.
The surface charge densities are σp and – σp. When we place the dielectric fully between the two plates of a capacitor, then it’s dielectric constant increases from its vacuum value.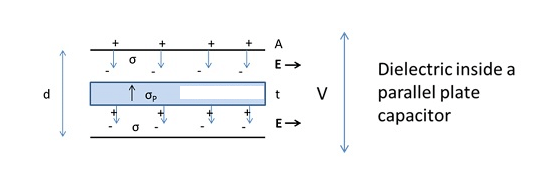
The electric field inside a capacitor is as follows:
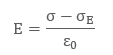
Hence we have:
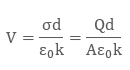
Therefore: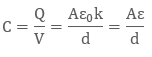
Ɛ is the permittivity of the substance. The potential difference between the plates is given by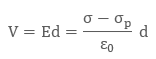
For linear dielectrics: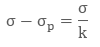
Where k is a dielectric constant of the substance, K = 1.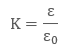
How does the dielectric increase the capacitance of a capacitor?
The electric field between the plates of parallel plate capacitor is directly proportional to capacitance C of the capacitor. The strength of the electric field is reduced due to the presence of dielectric. If the total charge on the plates is kept constant, then the potential difference is reduced across the capacitor plates. In this way, dielectric increases the capacitance of the capacitor.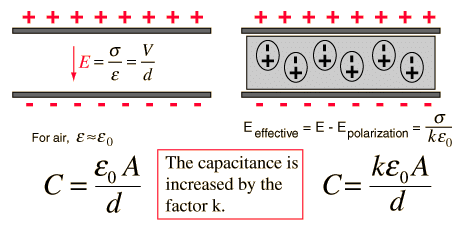
Capacitors with Dielectric
(i) In absence of dielectric
(ii) When a dielectric fills the space between the plates then molecules having dipole moment align themselves in the direction of electric field.
sb = induced charge density (called bound charge because it is not due to free electrons).
* For polar molecules dipole moment ¹ 0
* For non-polar molecules dipole moment = 0
(iii) Capacitance in the presence of dielectric

Here capacitance is increased by a factor K.
(iv) Polarisation of material :
When a non-polar substance is placed in an electric field then dipole moment is induced in the molecule. This induction of dipole moment is called polarisation of material. The induced charge also produces electric field.
σb = induced (bound) charge density.
It is seen the ratio of electric field between the plates in absence of dielectric and in presence of dielectric is constant for a material of dielectric. This ratio is called 'Dielectric constant' of that material. It is represented by er or k.
(v) If the medium is not filled between the plates completely then electric filed will be as shown in figure.
Case : (1)
The total electric field produced by bound induced charge on the dielectric outside the slab is zero because they cancel each other.
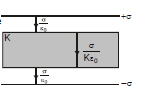
Case : (2)
so potential difference between plates
v =
so equivalent capacitance
C =
10.1 Introduction of a Dielectric slab of dielectric constant K between the plates
(a) When the battery is disconnected
Let q0, C0, V0, E0 and U0 represents the charge, capacity, potential difference, electric field and energy associated with charged air capacitor respectively. With the introduction of a dielectric slab of dielectric constant K between the plates and the battery disconnected.
(i) Charge remains constant, i.e., q = q0, as in an isolated system charge is conserved.
(ii) Capacity increases, i.e., C = KC0, as by the presence of a dielectric capacity becomes K times.
(iii) Potential difference between the plates decreases, i.e.,, as
[
q = q0 and C = KC0]
(iv) Field between the plates decreases, i.e., , as
[as
]
and
(v) Energy stored in the capacitor decreases i.e.
, as
(as q = q0 and C = KC0]
(b) When the battery remains connected (potential is held constant)
(i) Potential difference remains constant, i.e., V = V0, as battery is a source of constant potential difference.
(ii) Capacity increases, i.e., C = KC0, as by presence of a dielectric capacity becomes K times.
(iii) Charge on capacitor increases, i.e., q = Kq0, as
q = CV = (KC0)V = Kq0 [ q0 = C0V]
(iv) Electric field remains unchanged, i.e., E = E0, as
[as V = V0 and
]
(v) Energy stored in the capacitor increases, i.e., U = KU0, as
[as C = KC0 and
]
Solved Examples
Example.1 Assertion: In a circuit where two capacitors with capacitance C1 and C2 are connected in series with C1 followed by C2. A slab is inserted in C2. The potential difference across C2 will decrease.
Reason: The current flows in the clockwise direction, after the introduction of the slab.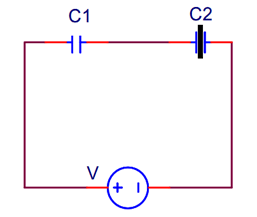
(a) Both the statements are correct and the reason is the correct explanation of the assertion.
(b) They both are correct but the reason is not the correct explanation of the assertion.
(c) The assertion is correct but the reason is not.
(d) The reason is correct but the assertion is not.
Solution: B) Upon inserting the slab, the value of C2 will increase to KC2. In series, V distributes in the inverse ratio of capacitance. As C2 increases, its potential will decrease. As C2 increases, the positive charge on both the capacitors will have to increase. Thus the current will flow in the clockwise direction.
Example.2 A parallel plate air capacitor is made using two square plates each of side 0.2 m, spaced 1 cm apart. It is connected to a 50V battery.
(a) What is the capacitance?
(b) What is the charge on each plate?
(c) What is the energy stored in the capacitor?
(d) What is the electric field between the plates?
(e) If the battery is disconnected and then the plates are pulled apart to a separation of 2 cm, what are the answers to the above parts?
Sol. (a)
(b) Q0 = C0V0 = 3.54 × 10-5 × 50 = 1.77 × 10-3 mC
(c)
(d)
(e) If the battery is disconnected the charge on the capacitor plates remains constant while the potential difference between the plates can change.
Q = Q0 = 1.77 × 10-3 mC
Example.3 In the last illustration, suppose that the battery is kept connected while the plates are pulled apart. What are the answers to the parts (a), (b), (c) and (d) in that case?
Sol. If the battery is kept connected, the potential difference across the capacitor plates always remains equal to the emf of battery and hence is constant.
V = V0 = 50V
Example.4 A parallel plate capacitor has plates of area 4 m2 separated by distance of 0.5 mm. The capacitor is connected across a cell of emf 100 V.
(a) Find the capacitance, charge and energy stored in the capacitor.
(b) A dielectric slab of thickness 0.5 mm is inserted inside this capacitor after it has been disconnected from the cell. Find the answers to part (a) if K = 3.
Sol. (a)
Q0 = C0V0 = (7.08 × 10-2 × 100)mC = 7.08 mC
(b) As the cell has been disconnected
Q = Q0
= 118 × 10-6 J
Example.5 If a dielectric slab of thickness t and area A is inserted in between the plates of a parallel plate capacitor of plate area A and distance between the plates d (d > t) then find out capacitance of system. What do you predict about the dependence of capacitance on location of slab ?
Sol.
(
t1 t2 = d - t)
* Capacitance does not depend upon the position of dielectric (it can be shifted up or down & still capacitance does not change).
* If the slab is of metal then
Example.6 Find out capacitance between A and B if two dielectric slabs of dielectric constant K1 and K2 of thickness d1 and d2 and each of area A are inserted between the plates of parallel plate capacitor of plate area A as shown in figure.
Sol. ;
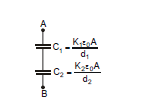
This formula suggests that the system between A and B can be considered as series combination of two capacitors.
Example.7 Find out capacitance between A and B if two dielectric slabs of dielectric constant K1 and K2 of area A1 and A2 and each of thickness d are inserted between the plates of parallel plate capacitor of plate area A as shown in figure.
Sol.
,
;
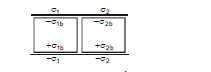
The combination is equivalent to :
Therefore, C = C1 C2
Example.8 Find out capacitance between A and B if three dielectric slabs of dielectric constant K1 of area A1 and thickness d1 K2 of area A2 and thickness d2 and K3 of area A2 and thickness d3 are inserted between the plates of parallel plate capacitor of plate area A as shown in figure. (Given distance between the two plates d = d1 d2)
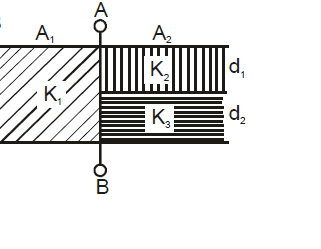
Sol. It is equivalent to
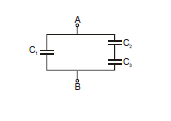
Example.9 A dielectric of constant K is slipπεd between the plates of parallel plate condenser in half of the space as shown in the figure. If the capacity of air condenser is C, then new capacitance between A and B will be
(A)
(B)
(C)
(D)
Sol. This system is equivalent to two capacitors in parallel with area of each plate.
|
268 videos|780 docs|209 tests
|
FAQs on Effect of Dielectric on Capacitance - Physics for JEE Main & Advanced
| 1. What are dielectrics and how do they affect capacitance? |  |
| 2. What are some examples of dielectric materials? |  |
| 3. How does the dielectric constant affect the capacitance? |  |
| 4. Can a dielectric material decrease the capacitance of a capacitor? |  |
| 5. How does the thickness of the dielectric material affect capacitance? |  |

















