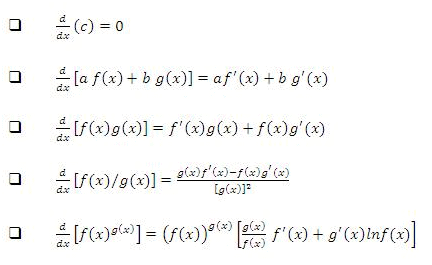JEE Exam > JEE Notes > Mock Tests for JEE Main and Advanced 2025 > Revision Notes - Differentiability
Differentiability Class 11 Notes Maths
- The derivative of f, denoted by f'(x) is given by f'(x) = lim?x→0 (? y)/(? x) = dy/dx
- The right hand derivative of f at x = a is denoted by f'(a+) and is given by f'(a+) = limh→0+(f(a+h)-f(a))/h
- The left hand derivative of f at x = a is denoted by f'(a-) and is given by f'(a-) = limh→0- (f(a-h)-f(a))/-h
- For a function to be differentiable at x=a, we should have f'(a-)=f'(a+) i.e. limh→0 (f (a-h)-f (a))/ (-h) = limh→0 (f (a+h)-f (a))/h.
- limh→0 sin 1/h fluctuates between -1 and 1.
- If at a particular point say x =a, we have f'(a+) = t1 (a finite number) and f'(a-) = t2 (a finite number) and if t1 ≠ t2, then f' (a) does not exist, but f(x) is a continuous function at x = a.
- Continuity and differentiability are quite interrelated.
Differentiability alwaysimpliescontinuity but the converse is not true. This means that a differentiable function is always continuous but if a function is continuous it may or may not be differentiable.
Some basic formulae:
- If a function is not derivable at a point, it need not imply that it is discontinuous at that point. But, however, discontinuity at a point necessarily implies non-derivability.
- In case, a function is not differentiable but is continuous at a particular point say x = a, then it geometrically implies a sharp corner at x = a.
- A function f is said to be derivable over a closed interval [a, b] if :
1. For the points a and b, f'(a+) and f'(b-) exist and
2. For ant point c such that a < c < b, f'(c+)and f'(c-) exist and are equal. - If y = f(u) and u = g(x), then dy/dx = dy/du.du/dx = f'(g(x)) g'(x). This method is also termed as the chain rule.
- For composite functions, differentiation is carried out in this way:
If y = [f(x)]n, then we put u = f(x). So that y = un. Then by chain rule:
dy/dx = dy/du.du/dx = nu(n-1)f' (x) = [f(x)](n-1) f' (x) - Differential calculus problems involving parametric functions:
If x and y are functions of parameter t, first find dx/dt and dy/dt separately. Then dy/dx=(dy/dt)/(dx/dt). - If the functions f(x) and g(x) are derivable at x = a, then the following functions are also derivable:
1.f(x) + g(x)
2.f(x) - g(x)
3.f(x) . g(x)
4.f(x) / g(x), provided g(a) ≠ 0 - If the function f(x) is differentiable at x =a while g(x) is not derivable at x = a, then the product function f(x). g(x) can still be differentiable at x = a.
- Even if both the functions f(x) and g(x) are not differentiable at x = a, the product function f(x).g(x) can still be differentiable at x = a.
- Even if both the functions f(x) and g(x) are not derivable at x = a, the sum function f(x) + g(x) can still be differentiable at x = a.
If function f(x) is derivable at x = a, this need not imply that f'(x) is continuous at x = a.
The document Differentiability Class 11 Notes Maths is a part of the JEE Course Mock Tests for JEE Main and Advanced 2025.
All you need of JEE at this link: JEE
|
357 docs|148 tests
|
FAQs on Differentiability Class 11 Notes Maths
| 1. What is the definition of differentiability? |  |
Ans. Differentiability is a property of a function that measures how smooth and well-behaved it is. A function is said to be differentiable at a point if its derivative exists at that point. The derivative represents the rate of change of the function at that point.
| 2. How is differentiability related to continuity? |  |
Ans. Differentiability is a stronger condition than continuity. While all differentiable functions are continuous, not all continuous functions are differentiable. A function is differentiable if and only if it is continuous and its derivative exists at every point in its domain.
| 3. Can a function be differentiable at one point but not at another? |  |
Ans. Yes, it is possible for a function to be differentiable at one point but not at another. Differentiability is a local property, meaning it is determined at each individual point. A function may have points where it is differentiable and points where it is not.
| 4. What is the significance of differentiability in calculus? |  |
Ans. Differentiability plays a crucial role in calculus as it allows us to determine important properties of functions, such as their rate of change, slope, and optimization. It enables us to find tangent lines, calculate derivatives, and solve optimization problems, making it a fundamental concept in calculus.
| 5. How can I determine if a function is differentiable? |  |
Ans. To determine if a function is differentiable at a point, you need to check if its derivative exists at that point. The derivative can be calculated using various methods such as the limit definition of the derivative or using differentiation rules. If the derivative exists, the function is differentiable at that point.
Related Searches