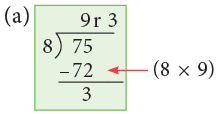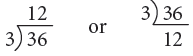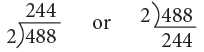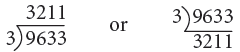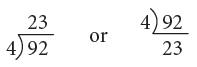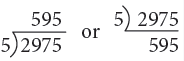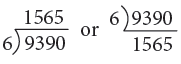Division Class 3 Notes Maths
Introduction
Have you ever shared a packet of chocolates with your friends? Imagine Yash's mother gave him 10 toffees. He decided to share the toffees equally with his four friends—Mohan, Anil, Jiten and Lakshya. How many toffees will each of them get? Let us find out:
Let us find out:
Yash gives 1 toffee to each friend including himself. Yash is left with five toffees to be distributed.
Yash is left with five toffees to be distributed. Yash gives one more toffee to each friend. Now, each of them has:
Yash gives one more toffee to each friend. Now, each of them has: Now, Yash is left with no toffees to be distributed.
Now, Yash is left with no toffees to be distributed.
You can see that each of them gets 2 toffees.
So, if we divide (share equally) 10 toffees among 5 people, each of them gets 2 toffees.
We can write this as a division fact, as shown below.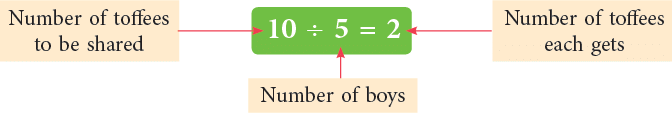
Parts of a Division Equation
A division equation has three parts: the dividend, the divisor and the quotient.
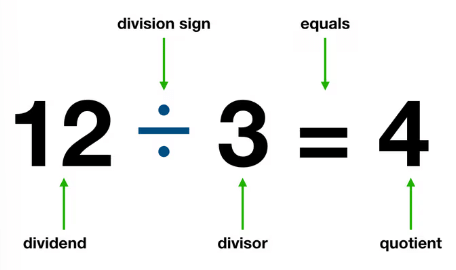
- The dividend is the number that is being divided, and it is usually larger.
- The divisor is the number that divides the dividend into equal parts, and it is typically smaller.
- The quotient is the answer we get after performing the division.
Division as Forming Equal Groups
Let us take 15 balls and divide them into groups of 5 balls each.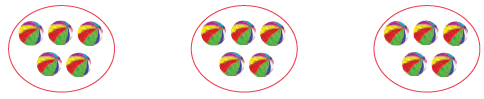 How many groups have you made?
How many groups have you made?
How many balls in each group?
We write the above division fact as: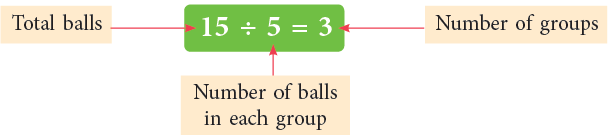
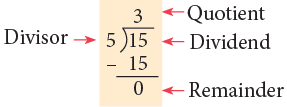
The terms that we use in a division fact are: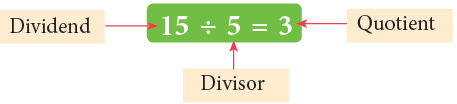
Division as Repeated Subtraction
Anand has 8 pieces of chocolate pastries. There are some guests coming for dinner at his house. He gives 2 pastries to each guest. How many guests are there at his house? Chocolate pastries remaining after giving 2 pieces to the first guest, 8 – 2 = 6.
Chocolate pastries remaining after giving 2 pieces to the first guest, 8 – 2 = 6. Chocolate pastries remaining after giving 2 pieces to the second guest, 6 – 2 = 4.
Chocolate pastries remaining after giving 2 pieces to the second guest, 6 – 2 = 4. Chocolate pastries remaining after giving 2 pieces to the third guest, 4 – 2 = 2.
Chocolate pastries remaining after giving 2 pieces to the third guest, 4 – 2 = 2. Chocolate pastries remaining after giving 2 pieces to his fourth guest, 2 – 2 = 0.
Chocolate pastries remaining after giving 2 pieces to his fourth guest, 2 – 2 = 0.
We can show how Anand distributed pastries to his guests as: Thus, we can see that 2 is subtracted from 8 four times. So, the number of guests to whom 2 pastries each are given is 4. This can be represented by a division fact as 8 ÷ 2 = 4.
Thus, we can see that 2 is subtracted from 8 four times. So, the number of guests to whom 2 pastries each are given is 4. This can be represented by a division fact as 8 ÷ 2 = 4.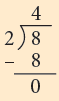
So, as multiplication is repeated addition, division is repeated subtraction.
Division on a Number Line
Look at the following. You skip count backwards by 3 until you reach 0. How many times do you have to skip count from 15 to 0? You make 5 skip counts.
You skip count backwards by 3 until you reach 0. How many times do you have to skip count from 15 to 0? You make 5 skip counts.
So,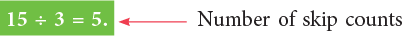
Relation between Multiplication and Division
Let us take an example to understand how multiplication and division are related.
Kavita has 6 stickers on a sheet of paper. She has arranged them as follows.
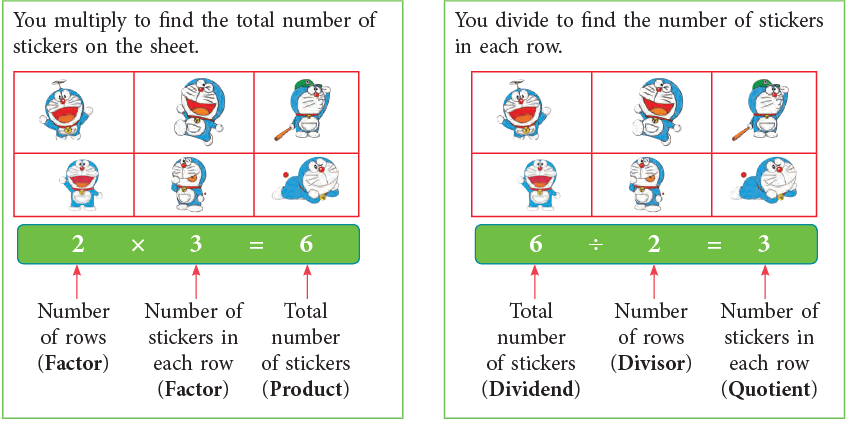 Thus, it can be concluded that
Thus, it can be concluded that
Division is opposite or inverse of multiplication.
Relation between division and multiplication fact can be shown on the number line as under:
Multiplication is like forward jumps on the number line.
Four forward jumps of 5 take you from 0 to 20.
Division is like backward jumps on the number line.
Four backward jumps of 5 take you from 20 to 0.
Example 1: Find 14 ÷ 2.
From the multiplication table of 2, you know that 2 × 7 = 14.
Think:
Therefore, 14 ÷ 2 = 7.
Properties of Division
1. Dividing by 1
See the given picture.
How many ones in 3?
Clearly, 3 ÷ 1 = 3.
Thus,
Any number divided by 1 gives the same number.
2. Dividing by the Number Itself
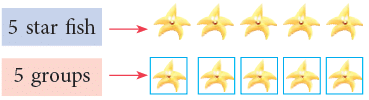 How many starfish are in each group?
How many starfish are in each group?
Clearly, there is 1 star fish in each group.
So, 5 ÷ 5 = 1.
Any number divided by itself is equal to 1.
3. Dividing Zero by a Number
Study the following examples.
0 ÷ 1 = 0 or 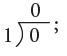
0 ÷ 5 = 0 or 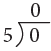
When you divide 0 by a number, the quotient is always 0.
4. Dividing a Number by Zero
Study the following examples.
5 ÷ 0 = ? or  7 ÷ 0 = ? or
7 ÷ 0 = ? or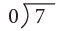
When you have zero as a divisor, the quotient is not defined.
Division using Multiplication Tables
You can use the multiplication table to divide.
To divide 42 ÷ 6, think that, 6 sevens are 42. Therefore,
42 ÷ 6 = 7 or 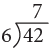
72 ÷ 8 = 9 or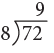
Think: 8 nines are 72.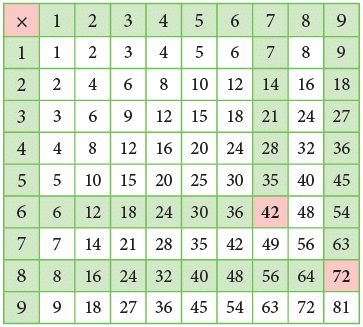
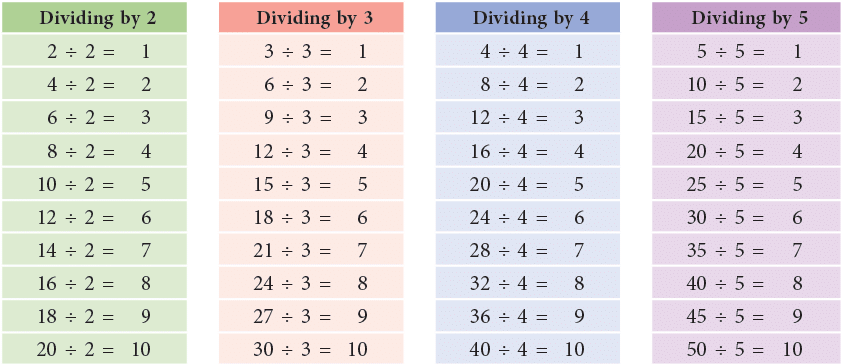
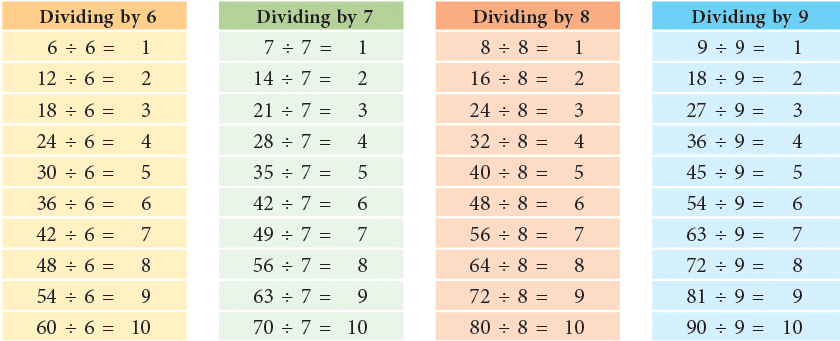
Basic Division Facts
Division with Remainder
A number does not always divide another number exactly. At times, there is a left over. The left over is called a remainder, written as r or R in short form.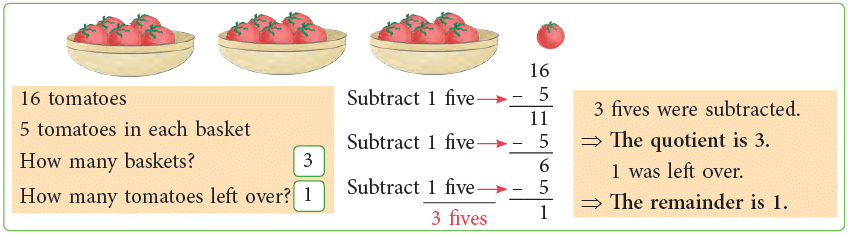 As the remainder is 1. So, one tomato is left over.
As the remainder is 1. So, one tomato is left over.
A shorter way is to subtract 3 fives in one step instead of subtracting it in three steps, as done here.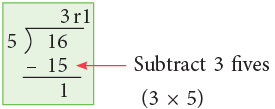
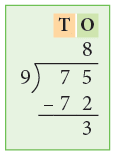
Example 2: Divide:
(a) 75 ÷ 8.
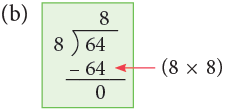
(b) 64 ÷ 8.
Thus, 75 ÷ 8 = 9r3.
Thus, 64 ÷ 8 = 8.
Checking Division
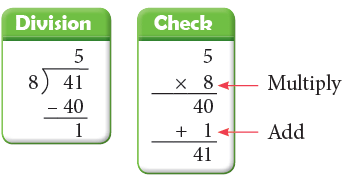
Rule: Multiply the quotient by the divisor and add the remainder to this product. The result should be the same as the dividend.
Divisor × Quotient + Remainder = Dividend
Example 3: Divide the following. Check your division.
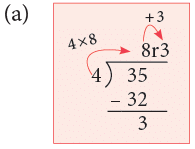
(a) 35 ÷ 4
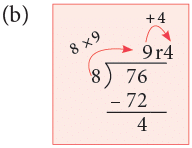
(b) 76 ÷ 8
Check:
4 × 8 + 3 = 35 = Dividend
Check:
8 × 9 + 4 = 76 = Dividend
Division by a 1-Digit Number (Without Remainder)
Consider 48 ÷ 4.
Method:
Step 1: Arrange the numbers, as shown.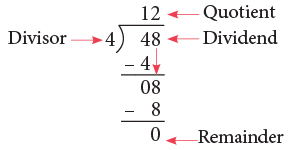
Step 2: Divide 4 tens by 4, 4 ÷ 4 = 1.
Write 1 in the tens place in the quotient and write 4 × 1 = 4 below 4 in the dividend.
Now, subtract 4 – 4 = 0.
Step 3: Bring down 8 ones and divide it by 4.
We get as 8 ÷ 4 = 2.
Write 2 in the ones place of the quotient and 4 × 2 = 8, below 8 in the dividend.
Now, subtract 8 – 8 = 0.
Thus, 48 ÷ 4 = 12.
Short Form: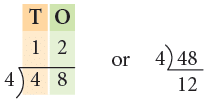
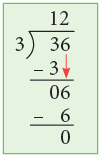
Example 4: Divide 36 by 3.
Thus, 36 ÷ 3 = 12.
Short Form:
Think:
Step 1: Divide the tens. 3 tens ÷ 3 = 1 ten.
Write 1 in the quotient at tens place.
Step 2: Divide the ones. 6 ones ÷ 3 = 2 ones.
Write 2 in the quotient at ones place.
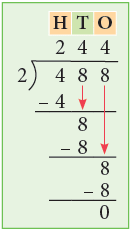
Example 5: Divide 488 by 2.
Thus, 488 ÷ 2 =244.
Short Method:
1.First, divide 4 hundreds by 2.
2. Next, divide 8 tens by 2.
3.Lastly, divide 8 ones by 2.
There is no remainder.
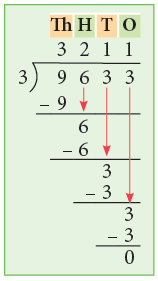
Example 6: Divide 9633 by 3.
Thus, 9633 ÷ 3 = 3211.
You may divide mentally and write as under.
Short Method:
1. First, divide 9 thousands by 3.
2. Next, divide 6 hundreds by 3.
3. Next, divide 3 tens by 3.
4. Lastly, divide 3 ones by 3.
There is no remainder.
Edurev Tips: Once you have practiced enough, then you should be able to divide using short form.
Division by Regrouping (Without Remainder)
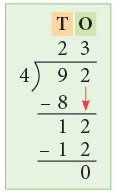
Example 7: Divide 92 by 4.
Thus, 92 ÷ 4 = 23.
Method:
Step 1: Divide 9 tens by 4.
Write 2 in the quotient at tens place and write 4 × 2 = 8, below 9.
Now, subtract 9 – 8 = 1.
Step 2:Bring down 2. Now 12 will be new dividend.
Divide 12 by 4. 4 goes into 12, 3 times.
Write 3 in the ones column above 2 and 4 × 3 = 12 below 12.
Now subtract 12 – 12 = 0.
Short Method:
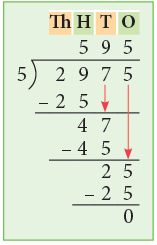
Example 8: Divide 2975 by 5.
Thus, 2975 ÷ 5 = 595.
Short Method:
2 < 5, so we consider 29, the number formed by the first two digits 2 and 9 of the dividend and divide it by 5. Using the multiplication table of 5, we see that 5 goes into 29, 5 times and yields 4 as a remainder. Write the quotient 5 above 9 of 29. Then, complete the division as shown by bringing down 7 and lastly bringing down the digit 5 of the dividend.
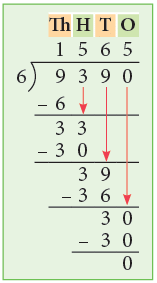
Example 9: Divide 9390 by 6.
Thus, 9390 ÷ 6 = 1565.
Short Method:
Step 1: First, divide 9 thousands by 6. You find that 6 goes into 9 one time. Write 1 in the thousands column of the quotient. Now subtract: 9 Th – 6 Th = 3 Th.
Step 2: Bring down 3 from hundreds making it 33 hundreds. 6 goes into 33 five times and yields remainder 3. Write 5 in the hundreds column of the quotient. Subtract: 33 H – 30 H = 3 H.
Step 3: Now, bring down 9 from tens place making it 39. 6 goes into 39 six times leaving remainder 3. Write 6 in the tens column of the quotient. Subtract: 39 T – 36 T = 3 T.
Step 4: Lastly, bring down 0 from ones place making it 30. 6 goes into 30 five times. Write 5 in the ones column of the quotient. Subtract:30 O – 30 O = 0 O.
Division by 10 and 100
Study the following.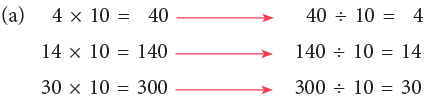
What do you notice?
Rule: To divide a number ending in zeros by 10, remove one zero from the right.
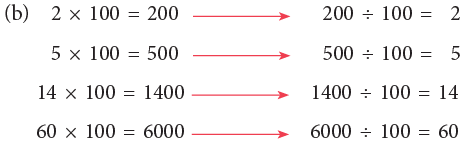
What do you notice?
Rule: To divide a number ending in zeros by 100, remove two zeros from the right.
Division by Regrouping (With Remainder)
Example 10: John is having a birthday party. He invited nine friends and his mother baked 75 cookies for the party. How many cookies did each friend get? How many cookies were left?
To find the number of cookies each friend gets, we divide 75 by 9. The remainder gives the number of left over cookies.
Thus, each friend gets 8 cookies and 3 cookies are left over.
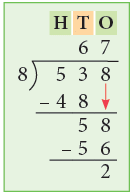
Example 11: Divide 538 by 8.
Thus, 538 ÷ 8 = 67r2.
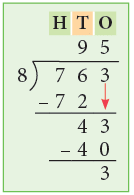
Example 12: Divide 763 by 8 and check the result.
Here, Divisor = 8, Quotient = 95, Remainder = 3, Dividend = 763
Check: Divisor × Quotient + Remainder
= 8 × 95 + 3 = 763
= Dividend
Thus, 763 ÷ 8 = 95r3.
Edurev Tips: (Divisor × Quotient) + Remainder = Dividend
Problems Based on Real Life Situations
Ques 1.
 Suppose there are 12 children such that 4 children are in each row.
Suppose there are 12 children such that 4 children are in each row.So how many rows are there in total?
Write:12 ÷ 4 = 3
Think: How many 4s in 12?
The division fact, 12 ÷ 4 = 3 answers this question.
Thus, 3 rows of 4 children each.
Ques 2. 1576 biscuit packets are to be distributed equally in 8 shops.
1576 biscuit packets are to be distributed equally in 8 shops.
How many biscuit packets will each shop receive?
To know the answer, we find 1576 ÷ 8 as shown on the right.
We have a quotient as 197.
So, each shop will receive 197 biscuit packets.
Working: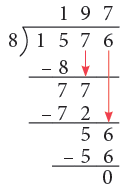
|
18 videos|120 docs|25 tests
|
FAQs on Division Class 3 Notes Maths
| 1. What are the basic parts of a division equation? |  |
| 2. How is division related to multiplication? |  |
| 3. What are some properties of division? |  |
| 4. How can I use multiplication tables to help with division? |  |
| 5. What does it mean to divide with a remainder? |  |