Introduction: Polynomials | Advance Learner Course: Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Polynomials |

|
| Types of Polynomials based on Degree |

|
| Types of Polynomials based on the Number of Terms |

|
| Polynomial Operations |

|
| Solved Examples |

|
Polynomials
Any expression that contains constants, variables as well as exponents which can be either added, subtracted, multiplied or divided.
But there is a catch, it must follow these rules:
1. Cannot have an infinite number of terms
2. A variable’s exponent can only be a whole number i.e., 0,1,2,3…etc.
3. Cannot be divisible by a variable
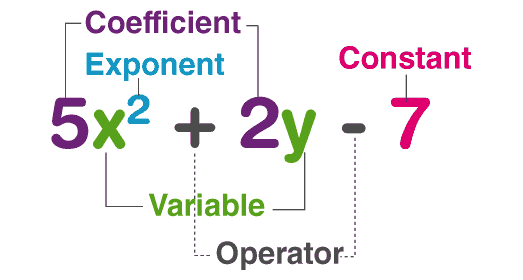 Polynomial
Polynomial
Degree of a Polynomial
If p(x) is a polynomial in x, the highest power of x in p(x) is called the degree of polynomial p(x).
Examples:
1. 3x4+2x2+6x = 1, the highest power of the given polynomial equation is 4. Therefore, its degree is 4.
2. x5y3z + 2xy3+4x2yz2
because this equation contains several variables ( that is, x,y, and z) we need to add up the degrees of the variables in each of the terms in order to find the degree of the variable. Please note, it does not matter if they are differing variables.
as a result, a 1st term (5+3+1), the 2nd term (1+3) and the 3rd term (2+1+2).
The highest total is 9, of the 1st term, consequently, its degree is 9.
Here's a video about Polynomials:
Types of Polynomials based on Degree
1. Linear Polynomial: Polynomial equation with degree 1 is called a linear polynomial.
Example: x – 3 = 0
2. Quadratic Polynomial: Polynomial equation with degree 2 is called a quadratic polynomial.
Example: x2+2x+7 = 0.
3.Cubic Polynomial: Polynomial equation with degree 3 is called a cubic polynomial.
Example: 3x3–5x2+7x+5 = 0.
Types of Polynomials based on the Number of Terms
1. Monomial: A polynomial with just one term.
Example: 2x, 6x2, 9xy
2. Binomial: A polynomial with two terms.
Example: 4x2+x, 5x+4
3. Trinomial: A polynomial with three terms.
Example: x2+3x+4
Polynomial Operations
There are four main polynomial operations which are:
- Addition of Polynomials
- Subtraction of Polynomials
- Multiplication of Polynomials
- Division of Polynomials
Each of the operations on polynomials is explained below using solved examples.
Addition of Polynomials
To add polynomials, always add the like terms, i.e. the terms having the same variable and power. The addition of polynomials always results in a polynomial of the same degree. For example,
Example: Find the sum of two polynomials: 5x3 + 3x2y + 4xy − 6y2 and 3x2 + 7x2y − 2xy + 4xy2 − 5
Solution:
First, combine the like terms while leaving the unlike terms as they are. Hence,
(5x3 + 3x2y + 4xy − 6y2) + (3x2 + 7x2y − 2xy +4xy2 −5)
= 5x3 + 3x2 + (3+7)x2y + (4−2)xy + 4xy2 − 6y2 − 5
= 5x3 + 3x2 + 10x2y + 2xy + 4xy2 − 6y2 − 5
Subtraction of Polynomials
Subtracting polynomials is similar to addition, the only difference being the type of operation. So, subtract the like terms to obtain the solution. It should be noted that subtraction of polynomials also results in a polynomial of the same degree.
Example: Find the difference of two polynomials: 5x3 + 3x2y + 4xy − 6y2, 3x2 + 7x2y − 2xy + 4xy2 − 5
Solution:
First, combine the like terms while leaving the unlike terms as they are. Hence,
(5x3 + 3x2y + 4xy −6y2) - (3x2 + 7x2y − 2xy + 4xy2 − 5)
= 5x3-3x2 + (3-7)x2y + (4+2)xy- 4xy2 − 6y2 + 5
= 5x3 - 3x2 - 4x2y + 6xy - 4xy2 − 6y2 + 5
Multiplication of Polynomials
Two or more polynomial when multiplied always result in a polynomial of higher degree (unless one of them is a constant polynomial). An example of multiplying polynomials is given below:
Example: Solve (6x − 3y)x(2x + 5y)
Solution:
⇒ 6x ×(2x + 5y)–3y × (2x + 5y) ———- Using distributive law of multiplication
⇒ (12x2 + 30xy) – (6yx + 15y2) ———- Using distributive law of multiplication
⇒12x2 + 30xy – 6xy – 15y2 —————– as xy = yx
Thus, (6x−3y)×(2x+5y)=12x2+24xy−15y2
Division of Polynomials
Division of two polynomial may or may not result in a polynomial. Let us study below the division of polynomials in details. To divide polynomials, follow the given steps:
Polynomial Division Steps:
If a polynomial has more than one term, we use the long division method for the same. Following are the steps for it.
- Write the polynomial in descending order.
- Check the highest power and divide the terms by the same.
- Use the answer in step 2 as the division symbol.
- Now subtract it and bring down the next term.
- Repeat step 2 to 4 until you have no more terms to carry down.
- Note the final answer, including remainder, will be in the fraction form (last subtract term).
Solved Examples
Example:
Given two polynomial 7s3+2s2+3s+9 and 5s2+2s+1.
Solve these using mathematical operation.
Solution:
Given polynomial:
7s3+2s2+3s+9 and 5s2+2s+1
Polynomial Addition: (7s3+2s2+3s+9) + (5s2+2s+1)
= 7s3+(2s2+5s2)+(3s+2s)+(9+1)
= 7s3+7s2+5s+10
Hence, addition result in a polynomial.
Polynomial Subtraction: (7s3+2s2+3s+9) – (5s2+2s+1)
= 7s3+(2s2-5s2)+(3s-2s)+(9-1)
= 7s3-3s2+s+8
Hence addition result in a polynomial.
Polynomial Multiplication:(7s3+2s2+3s+9) × (5s2+2s+1)
= 7s3 (5s2+2s+1)+2s2 (5s2+2s+1)+3s (5s2+2s+1)+9 (5s2+2s+1))
= (35s5+14s4+7s3)+ (10s4+4s3+2s2)+ (15s3+6s2+3s)+(45s2+18s+9)
= 35s5+(14s4+10s4)+(7s3+4s3+15s3)+ (2s2+6s2+45s2)+ (3s+18s)+9
= 35s5+24s4+26s3+ 53s2+ 21s +9
Polynomial Division: (7s3+2s2+3s+9) ÷ (5s2+2s+1)
(7s3+2s2+3s+9)/(5s2+2s+1)
This cannot be simplified. Therefore, the division of these polynomials does not result in a polynomial.
Other topics covered under Polynomials:
Geometrical Meaning of the Zeroes of a Polynomial
|
13 videos|79 docs|29 tests
|
FAQs on Introduction: Polynomials - Advance Learner Course: Mathematics (Maths) Class 9
| 1. What are the different types of polynomials based on their degree? |  |
| 2. How are polynomials classified based on the number of terms they have? |  |
| 3. What are some common operations performed on polynomials? |  |
| 4. Can you provide an example of a linear polynomial? |  |
| 5. How can polynomials be useful in real-life applications? |  |
















