Irodov Solutions: Dynamics of A Solid Body- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 234. A thin uniform rod AB of mass m = 1.0 kg moves translationally with acceleration w = 2.0 m/s2 due to two antiparallel forces F1 a nd F2 (Fig. 1.52). The distance between the points at which these forces are applied is equal to a = 20 cm. Besides, it is known that F2 = 5.0 N. Find the length of the rod.
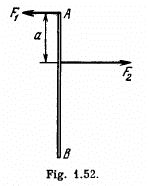
Ans. Since, motion of the rod is purely translational, net torque about the C.M. of the rod should be equal to zero.
Thus 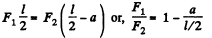 (1)
(1)
For the translational motion of rod.
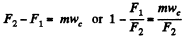 (2)
(2)
From (1) and (2)
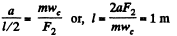
Q. 235. A force F = Ai + Bj is applied to a point whose radius vector relative to the origin of coordinates O is equal to r = ai + bj, where a, b, A, B are constants, and i, j are the unit vectors of the x and y axes. Find the moment N and the arm l of the force F relative to the point O.
Ans. Sought moment
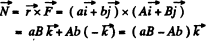
and arm of the force 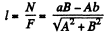
Q. 236. A force F1 = Aj is applied to a point whose radius vector r1 = ai, while a force F2 = Bi is applied to the point whose radius vector r2 = bj. Both radius vectors are determined relative to the origin of coordinates O, i and j are the unit vectors of the x and y axes, a, b, A, B are constants. Find the arm l of the resultant force relative to the point O.
Ans. Relative to point O, the net moment of force :
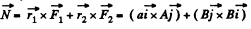
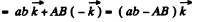 (1)
(1)
Resultant of the external force
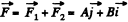 (2)
(2)
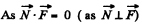 so the sought arm l o f the force
so the sought arm l o f the force 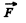
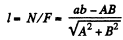
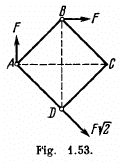
Q. 237. Three forces are applied to a square plate as shown in Fig. 1.53. Find the modulus, direction, and the point of application of the resultant force, if this point is taken on the side BC.
Ans. For coplanar forces, about any point in the same plane 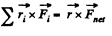
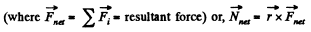
Thus length of the arm, 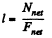
Here obviously 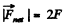 and it is directed toward right along AC. Take the origin at C. Then about C,
and it is directed toward right along AC. Take the origin at C. Then about C,
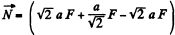 directed normally into the plane of figure.
directed normally into the plane of figure.
(Here a = side of the square.)
Thus 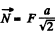 directed into the plane of the figure.
directed into the plane of the figure.
Hence 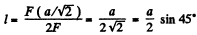
Thus the point of application of force is at the mid point of the side BC.
Q. 238. Find the moment of inertia
(a) of a thin uniform rod relative to the axis which is perpendicular to the rod and passes through its end, if the mass of the rod is m and its length l;
(b) of a thin uniform rectangular plate relative to the axis passing perpendicular to the plane of the plate through one of its vertices, if the sides of the plate are equal to a and b, and its mass is m.
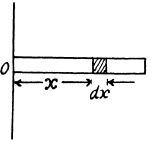
Ans. (a) Consider a strip of length dx at a perpendicular distance x from the axis about which we have to find the moment of inertia of the rod. The elemental mass of the rod equals
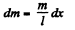
Moment of inertia of this element about the axis
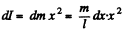
Thus, moment of inertia of the rod, as a whole about the given axis
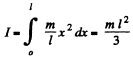
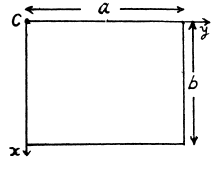
(b) Let us imagine the plane of plate as xy plane taking the origin at the intersection point of the sides of the plate (Fig.).
Obviously 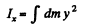
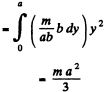
Similarly 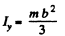
Hence from perpendicular axis theorem
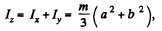
which is the sought moment of inertia.
Q. 239. Calculate the moment of inertia
(a) of a copper uniform disc relative to the symmetry axis perpendicular to the plane of the disc, if its thickness is equal to b = 2.0 mm and its radius to R = 100 mm;
(b) of a uniform solid cone relative to its symmetry axis, if the mass of the cone is equal to m and the radius of its base to R.
Ans. (a) Consider an elementry disc of thickness dx. Moment of inertia of this element about the 2 -axis, passing through its C.M.
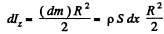
where p = density of the material of the plate and S = area of cross section of the plate.
Thus the sought moment of inertia
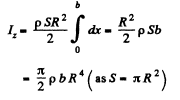
putting all the vallues we get,lz = 2.gm.m2
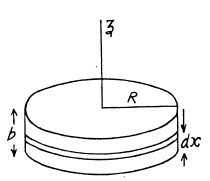
(b) Consider an element disc of radius r and thickness dx at a distance x from the point O. Then r = x tana and volume of the disc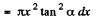
Hence, its mass dm = πx2 tan α dx.p (where p = density of the cone 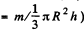
Moment of inertia of this element, about the axis OA,
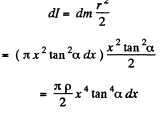
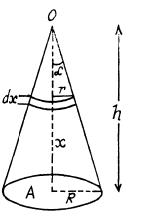
Thus the sought moment of inertia 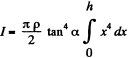
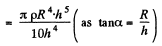
Hence 
Q. 240. Demonstrate that in the case of a thin plate of arbitrary shape there is the following relationship between the moments of inertia: l1 + I2 = l., where subindices 1, 2, and 3 define three mutually perpendicular axes passing through one point, with axes 1 and 2 lying in the plane of the plate. Using this relationship, find the moment of inertia of a thin uniform round disc of radius R and mass m relative to the axis coinciding with one of its diameters.
Ans. (a) Let us consider a lamina of an arbitrary shape and indicate by 1,2 and 3, three axes coinciding with x, y and z - axes and the plane o f lamina as x - y plane.
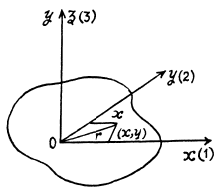
Now, moment of inertia of a point mass about
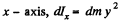
Thus moment of inertia of the lamina about
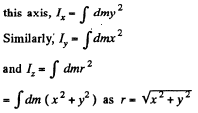
Thus, 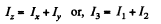
(b) Let us take the plane of the disc as x - y plane and origin to the centre of the disc (Fig.) From the symmetry Ix = Iy. Let us consider a ring element of radius r and thickness dr, then the moment of inertia of the ring element about the y - axis. \
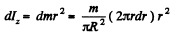
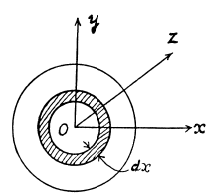
Thus the moment of inertia of the disc about
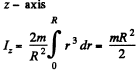
But we have 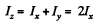
Thus 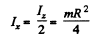
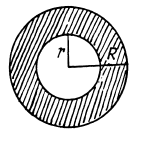
Q. 241. A uniform disc of radius R = 20 cm has a round cut as shown in Fig. 1.54. The mass of the remaining (shaded) portion of the disc equals m = 7.3 kg. Find the moment of inertia of such a disc relative to the axis passing through its centre of inertia and perpendicular to the plane of the disc.
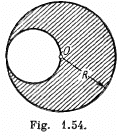
Ans. For simplicity let us use a mathematical trick. We consider the portion of the given disc as the superposition of two- complete discs (without holes), one of positive density and radius R and other of negative density but of same magnitude and radius R/2.
As (area) α (mass), the respective masses of the considered discs are (4m/3) and (-m/3) respectively, and these masses can be imagined to be situated at their respective centers (C.M). Let us take point O as origin and point x - axis towards right Obviously the C.M. of the shaded position of given shape lies on the x - axis. Hence the C.M. (C) of the shaded portion is given by
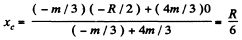
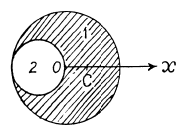
Thus C.M. of the shape is at a distance R/6 from point O toward x - axis
Using parallel axis theorem and bearing in mind that the moment of inertia of a complete homogeneous disc of radius m0 and radius r0 equals 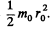
The moment of inetia of the small disc of mass (- m / 3) and radius R / 2 about the axis passing through point C and perpendicular to the plane of the disc
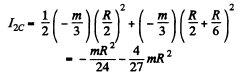
Simflarly
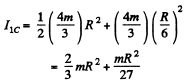
Thus the sought moment of inertia,
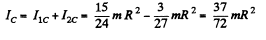
Q. 242. Using the formula for the moment of inertia of a uniform sphere, find the moment of inertia of a thin spherical layer of mass m and radius R relative to the axis passing through its centre.
Ans. Moment of inertia of the shaded portion, about the axis passing through it ’s certre,
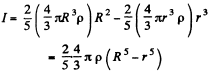
Now, if R = r + dr, the shaded portion becomes a shell, which is the required shape to calculate the moment of inertia.
Now, 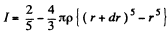
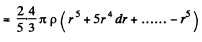
Neglecting higher terms,
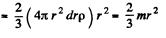
Q. 243. A light thread with a body of mass m tied to its end is wound on a uniform solid cylinder of mass M and radius R (Fig. 1.55). At a moment t = 0 the system is set in motion. Assuming the friction in the axle of the cylinder to be negligible, find the time dependence of
(a) the angular velocity of the cylinder;
(b) the kinetic energy of the whole system.
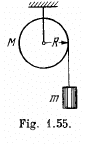
Ans. (a) Net force which is effective on the system (cylinder M + body m) is the weight of the body m in a uniform gravitational field, which is a constant. Thus the initial acceleration of the body m is also constant.
From the conservation of mechanical energy of the said system in the uniform field of gravity at time 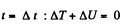
or 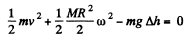
or, 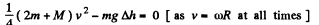
But 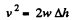
Hence using it in Eq. (1), we get
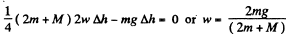
From the kinematical relationship, 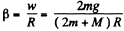
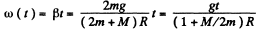
(b) Sought kinetic energy.
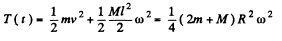
Q. 244. The ends of thin threads tightly wound on the axle of radius r of the Maxwell disc are attached to a horizontal bar. When the disc unwinds, the bar is raised to keep the disc at the same height. The mass bf the disc with the axle is equal to m, the moment of inertia of the arrangement relative to its axis is I. Find the tension of each thread and the acceleration of the bar.
Ans. For equilibrium of the disc and axle
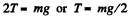
As the disc unwinds, it has an angular acceleration β given by
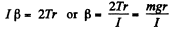
The corresponding linear acceleration is 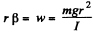
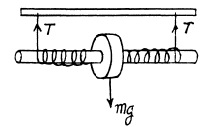
Since the disc remains stationary under the combined action of this acceleration and the acceleration (-w) of the bar which is transmitted to the axle, we must have 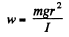
Q. 245. A thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment the end B starts experiencing a constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle op counted relative to the initial position.
Ans. Let the rod be deviated through an angle φ'from its initial position at an arbitrary instant of time, measured relative to the initial position in the positive direction. From the equation of the increment of the mechanical energy of the system.
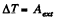
or, 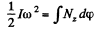
or, 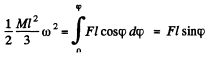
Thus, 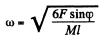
Q. 246. In the arrangement shown in Fig. 1.56 the mass of the uniform solid cylinder of radius R is equal to m and the masses of two bodies are equal to m1 and m2. The thread slipping and the friction in the axle of the cylinder are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions T1/T2 of the vertical sections of the thread in the process of motion.
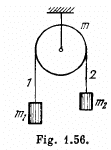
Ans. First of all, let us sketch free body diagram of each body. Since the cylinder is rotating and massive, the tension will be different in both the sections of threads. From Newton’s law in projection form for the bodies m1 and m2 and noting that w1 = w2 = βR, (as no thread slipping), we have (m1 > m2)

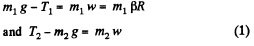
Now from the equation of rotational dynamics of a solid about stationary axis of rotation, i.e.
Nz = I βz, for the cylinder.
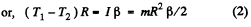
Similtaneous solution of the above equations yields :
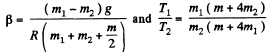
Q. 247. In the system shown in Fig. 1.57 the masses of the bodies are known to be m1 and m2, the coefficient of friction between the body mi and the horizontal plane is equal to k, and a pulley of mass m is assumed to be a uniform disc. The thread does not slip over the pulley. At the moment t = 0 the body m2 starts descending. Assuming the mass of the thread and the friction in the axle of the pulley to be negligible, find the work performed by the friction forces acting on the body m1 over the first t seconds after the beginning of motion.
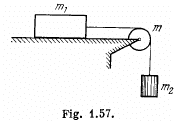
Ans. As the systenr (m + m1 + m2) is under constant forces, the acceleration of body m1 an m2 is constant In addition to it the velocities and accelerations of bodies m1 and m2 equal in magnitude (say v and tv) because the length of the thread is constant From the equation of increament of mechanical energy i.e. ΔT + ΔU = Afr, at time t whe block m1 is distance h below from initial position corresponding to t = 0,
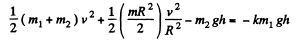 (1
(1
(as angular velocity ω - v/R for no slipping of thread.)
But v2 = 2wh
So using it in (1), we get 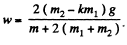 (2
(2
Thus the work done by the friction force on m1
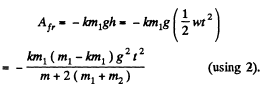
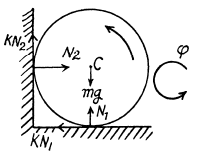
Q. 248. A uniform cylinder of radius R is spinned about its axis to the angular velocity ω0 and then placed into a corner (Fig. 1.58). The coefficient of friction between the corner walls and the cylinder is equal to k. How many turns will the cylinder accomplish before it stops?
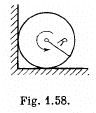
Ans. In the problem, the rigid body is in translation equlibrium but there is an angular retardation. We first sketch the free body diagram of the cylinder. Obviously the friction forces, acting on the cylinder, are kinetic. From the condition of translational equlibrium for the cylinder,
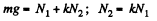
Hence, 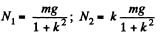
For pure rotation‘of the cylinder about its rotation axis, Nz - Iβz
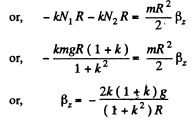
Now, from the kinematical equation,
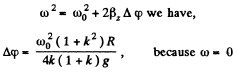
Hence, the sought number of turns,
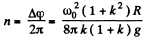
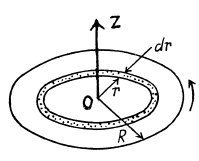
Q. 249. A uniform disc of radius R is spinned to the angular velocity ω and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coefficient is equal to k? The pressure exerted by the disc on the surface can be regarded as uniform.
Ans. It is the moment of friction force which brings the disc to rest The force of friction is applied to each section of the disc, and since these sections lie at different distances from the axis, the moments of the forces of friction differ from section to section.
To find Nz, where z is the axis of rotation of the disc let us partition the disc into thin rings (Fig.). The force of friction acting on the considered element 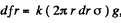 (where σ is the density of the disc)
(where σ is the density of the disc)
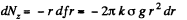
Integrating with respect to r from zero to R, we get
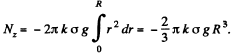
For the rotation of the disc about the stationary axis z, from the equation Nz = Iβz
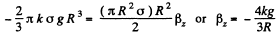
Thus from the angular kinematical equation
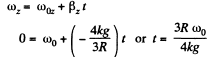
Q. 250. A flywheel with the initial angular velocity ω0 decelerates due to the forces whose moment relative to the axis is proportional to the square root of its angular velocity. Find the mean angular velocity of the flywheel averaged over the total deceleration time.
Ans. According to the question,
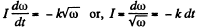
Integrating, 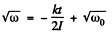
or, 
Let the flywheel stops at t = t0 then from Eq. 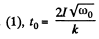
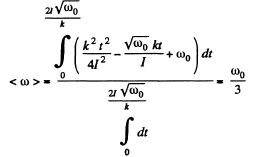
Hence sought average angular velocity
FAQs on Irodov Solutions: Dynamics of A Solid Body- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are the key topics covered in the Irodov Solutions: Dynamics of a Solid Body - 1 NEET article? |  |
| 2. How can I prepare for the Dynamics of a Solid Body section in the NEET exam? |  |
| 3. What are the common mistakes students make while solving dynamics problems in the NEET exam? |  |
| 4. Are there any specific strategies to solve dynamics problems quickly and accurately in the NEET exam? |  |
| 5. Where can I find additional resources or practice questions for Dynamics of a Solid Body for the NEET exam? |  |





















