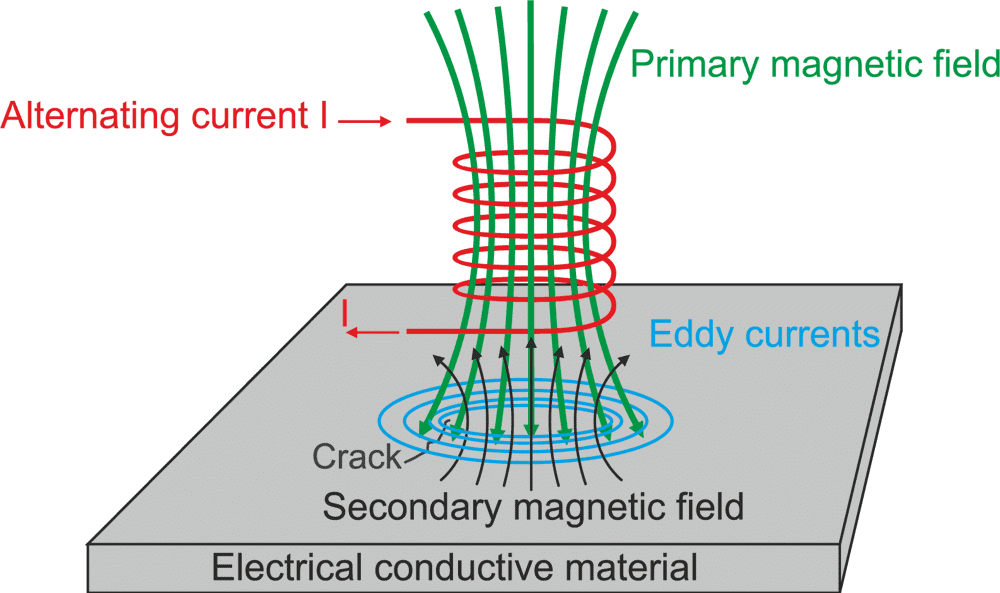
Eddy Currents | Physics for JEE Main & Advanced PDF Download
What are Eddy Currents?
- An eddy current is a current set up in a conductor in response to a changing magnetic field. They flow in closed loops in a plane perpendicular to the magnetic field. By Lenz law, the current swirls in such a way as to create a magnetic field opposing the change; for this to occur in a conductor, electrons swirl in a plane perpendicular to the magnetic field.
- Because of the tendency of eddy currents to oppose, eddy currents cause a loss of energy. Eddy currents transform more useful forms of energy, such as kinetic energy, into heat, which isn’t generally useful.
 Formation of Eddy Currents
Formation of Eddy Currents
Some Practical Applications
In the Brakes of Trains
During braking, the brakes expose the metal wheels to a magnetic field which generates eddy currents in the wheels. The magnetic interaction between the applied field and the eddy currents acts to slow the wheels down. The faster the wheels spin, the stronger is the effect, meaning that as the train slows the braking force is reduces, producing a smooth stopping motion.
Electromagnetic damping
- Used to design deadbeat galvanometers. Usually, the needle oscillates a little about its equilibrium position before it comes to rest. This causes a delay in taking the reading so to avoid this delay, the coil is wound over a non-magnetic metallic frame.
- As the coil is deflected, eddy currents set up in the metallic frame and thus, the needle comes to rest almost instantly.
- Thus, the motion of the “coil is damped”. Certain galvanometers have a fixed core made up of nonmagnetic metallic material. When the coil oscillates, the eddy currents that generate in the core oppose the motion and bring the coil to rest.
Electric Power Meters
The shiny metal disc in the electric power meter rotates due to eddy currents. The magnetic field induces the electric currents in the disc. You can also observe the shiny disc at your house.
 Electric power meters
Electric power meters
Induction Furnace
In a rapidly changing magnetic fields, due to a large emf produced, large eddy currents are set up. Eddy currents produce temperature. Thus a large temperature is created. So a coil is wound over a constituent metal which is placed in a field of the highly oscillating magnetic field produced by high frequency.  Industrial induction furnace
Industrial induction furnace
The temperature produced is enough to melt the metal. This is used to extract metals from ores. Induction furnace can be used to prepare alloys, by melting the metals at a very high temperature.
Speedometers
To know the speed of any vehicle, these currents are used. A speedometer consists of a magnet which keeps rotating according to the speed of our vehicle. Eddy currents are been produced in the drum. As the drum turns in the direction of the rotating magnet, the pointer attached to the drum indicates the speed of the vehicle SpeedometerQues: Eddy currents are produced in a metallic conductor when
SpeedometerQues: Eddy currents are produced in a metallic conductor when
(a) The magnetic flux linked with it changes
(b) It is placed in the changing magnetic field
(c) Placed in the magnetic field
(d) Both A and B
Ans: D
Solution: They are produced when the magnetic flux passing through the metal object continuously changes. This may happen due to many reasons.
1. The object is placed in the region with changing magnetic field.
2. The object continuously moves in and out of the magnetic field region.
Power dissipation of eddy currents
Under certain assumptions (uniform material, uniform magnetic field, no skin effect, etc.) the power lost due to eddy currents per unit mass for a thin sheet or wire can be calculated from the following equation:
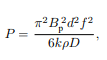 where
where
P is the power lost per unit mass (W/kg),
Bp is the peak magnetic field (T),
d is the thickness of the sheet or diameter of the wire (m),
f is the frequency (Hz),
k is a constant equal to 1 for a thin sheet and 2 for a thin wire,
ρ is the resistivity of the material (Ω m), and
D is the density of the material (kg/m3).
This equation is valid only under the so-called quasi-static conditions, where the frequency of magnetisation doe snot result in the skin effect; that is, the electromagnetic wave fully penetrates the material.
Diffusion Equation
The derivation of a useful equation for modelling the effect of eddy currents in a material starts with the differential, magnetostatic form of Ampère’s Law, providing an expression for the magnetizing field H surrounding a current density J:
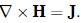
Taking the curl on both sides of this equation and then using a common vector calculus identity for the curl of the curl results in
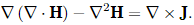
From Gauss’s law for magnetism, ∇ ·H = 0, so

Using Ohm’s law, J = σE, which relates current density J to electric field E in terms of a material’s conductivityσ,and assuming isotropic homogeneous conductivity, the equation can be written as
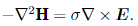
Using the differential form of Faraday’s law, ∇ × E = −∂B/∂t, this gives
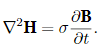
By definition, B = μ0(H+M), where M is the magnetization of the material and μ0 is the vacuum permeability. The diffusion equation therefore is
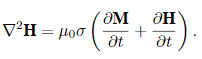
|
289 videos|635 docs|179 tests
|
FAQs on Eddy Currents - Physics for JEE Main & Advanced
| 1. What are eddy currents? |  |
| 2. How are eddy currents generated? |  |
| 3. What are the practical applications of eddy currents? |  |
| 4. How do eddy currents affect electrical transformers? |  |
| 5. Can eddy currents be used for levitation? |  |

|
Explore Courses for JEE exam
|

|