Mechanical Engineering Exam > Mechanical Engineering Notes > Theory of Machines (TOM) > Effect of Damping
Effect of Damping | Theory of Machines (TOM) - Mechanical Engineering PDF Download
Damped Systems
- Damping is an effect which causes a Reduction in the amplitude of an oscillation as a Result of energy being drained from the system to overcame frictional/other Resistive forces.
- These are the systems in which kinetic friction is zero. Technical Name of Kinetic friction in any Vibrations system is known as, Damping.
Damping in Any System
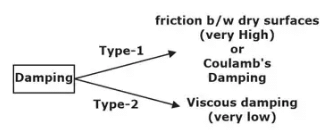
Damping force ox = (x = velocity)
= c·x
Where, c = coefficient of damping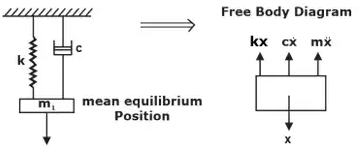
The equilibrium equation of a damped spring-mass system is given as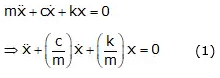
It is a 2nd order differential equation.
Types of Damping Systems
- Overdamped System(ζ>1)
No vibrations will be present in an over-damped system.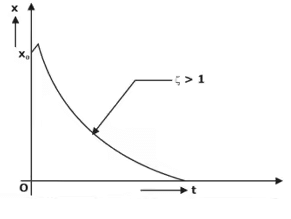 Critically Damped Systems(ζ = 1):
Critically Damped Systems(ζ = 1):
∴ No Vibrations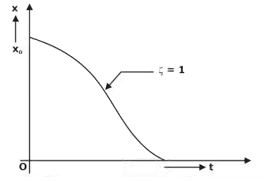 Note: Critical damping response is much faster than overdamping response i.e. in critically-damped systems, the body once displaced comes into its Equilibrium Position much faster than that in overdamped systems.
Note: Critical damping response is much faster than overdamping response i.e. in critically-damped systems, the body once displaced comes into its Equilibrium Position much faster than that in overdamped systems. - Under Damped Systems (ζ < 1)
∴ Damped frequency, ωd = ωn(1 - ξ2)1/2
Time period Td = 2π/wd (Second)
Linear frequency, fn = 1/Td (Hz)
Hence, Amplitude of under-Damped Vibrations is not constant and it decreases exponentially w.r.t. time.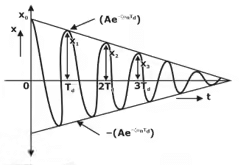
- Logarithmic Decrement (δ)
δ = In (Decrement ratio)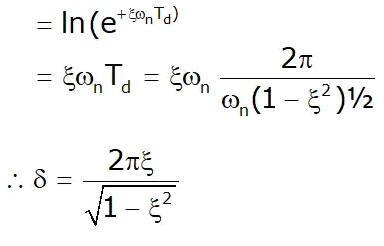
The document Effect of Damping | Theory of Machines (TOM) - Mechanical Engineering is a part of the Mechanical Engineering Course Theory of Machines (TOM).
All you need of Mechanical Engineering at this link: Mechanical Engineering
|
87 videos|85 docs|29 tests
|
Related Searches
















