Electric Potential Energy: Derivations | Additional Study Material for JEE PDF Download
Electric Potential Energy in An External Field
➤ Potential Energy of a Single Charge
Potential energy of q at r in an external field:
U = q.V(r),
where V(r) is the external potential at the point r.
➤ Potential Energy of a System of two Charges in an External Field
First, we calculate the work done in bringing the charge q1 from infinity to r1.
Next, we consider the work done in bringing q2 to r2. In this step, work is done not only against the external field E but also against the field due to q1.
- Work done on q2 against the external field = q2.V(r2)
- Work done on q2 against the field due to q1
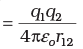
where r12 is the distance between q1 and q2. - By the superposition principle for fields, we add up the work done on q2 against the two fields (E and that due to q1):
Work done in bringing q2 to r2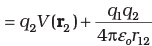
Thus, Potential energy of the system = Total work done in assembling the configuration
⇒ Potential Energy of the System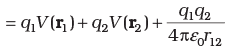
➤ Electric Potential Energy of a Dipole in an External Field
- Consider a dipole with charges q1 = +q and q2 = –q placed in a uniform electric field E, as shown in Figure below.
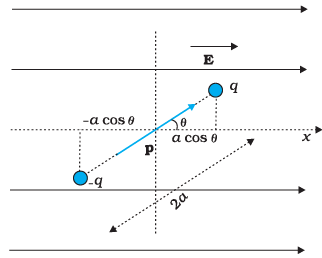
- In a uniform electric field, the dipole experiences no net force; but experiences a torque τ given by τ = p × E, which will tend to rotate it (unless p is parallel or anti-parallel to E).
- Suppose an external torque τext is applied in such a manner that it just neutralizes this torque and rotates it in the plane of paper from angle θ0 to angle θ1 at an infinitesimal angular speed and without angular acceleration.
- The amount of work done by the external torque will be given by:
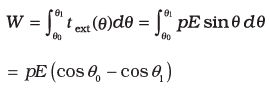
- This work is stored as the potential energy of the system. We can then associate potential energy U (θ) with an inclination θ of the dipole.
- Similar to other potential energies, there is freedom in choosing the angle where the potential energy U is taken to be zero. A natural choice is to take θ0 = π / 2. (Αn explanation for it is provided towards the end of discussion)
- We can then write,
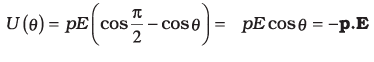
- On comparing with the case of System of two Charges in an External Field.
The potential energy expression is: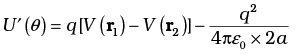
Here, r1 and r2 denote the position vectors of +q and –q. - Now, the potential difference between positions r1 and r2 equals the work done in bringing a unit positive charge against the field from r2 to r1.
- The displacement parallel to the force is 2a cosθ. Thus, [V(r1)–V (r2)] = –E × 2a cosθ.
We thus obtain: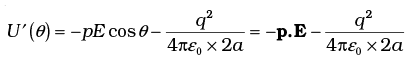
- We note that U′ (θ) differs from U (θ) by a quantity which is just a constant for a given dipole. We can now understand why we took θ0 = π/2. In this case, the work done against the external field E in bringing +q and – q are equal and opposite and cancel out, i.e., q [V(r1) – V (r2)] = 0.
Electric Potential Energy of Charged Particles
➤ Electric Potential Energy of a System of Two Charged Particles
- The figure shows two + ve charges q1 and q2 separated by a distance r. The electrostatic interaction energy of this system can be expressed as work done in bringing charge q2 from infinity to the given separation from q1.
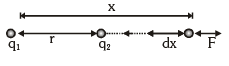
- It can be calculated as:
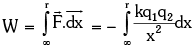 , where – ve sign shows that x is decreasing.
, where – ve sign shows that x is decreasing.
- If the two charges are of opposite signs, then potential energy will be negative as:
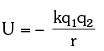
➤ Electric Potential Energy for a System of Multiple Charged Particles
- When more than two charged particles are there in a system, the interaction energy can be given as the sum of interaction energies of all the different possible pairs of particles.
- Example: If a system of three particles having charges q1, q2 and q3 is given as shown in figure.
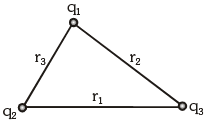 The total interaction energy of this system can be given as:
The total interaction energy of this system can be given as:
Electric Potential due to Sphere
➤ Electric Potential Due to a Conducting Sphere or a Shell

- Outside the Sphere: According to definition, Electric potential at the point P
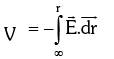
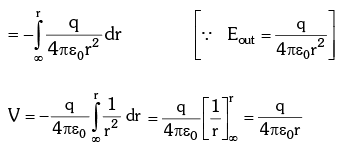
- On the Sphere:

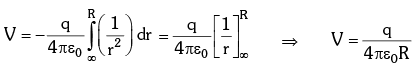
- Inside the Sphere:
∵ Inside the surface E = 0 , dV/dr = 0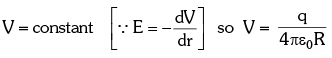
➤ Electric Potential Due to Solid Non-Conducting Sphere
- Outside the sphere: Same as conducting sphere.
- On the Surface: Same as conducting sphere.
- Inside the sphere:

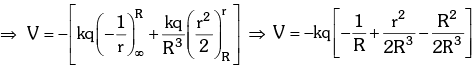
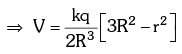
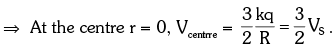
Electric Potential of Uniformly Charged Ring, Rod, and Disc
➤ Electric Potential Due to a Uniformly Charged Rod
Electric Potential due to a uniformly charged rod of length L and linear charge density lambda, at a point P on its axial line which is d units away from it.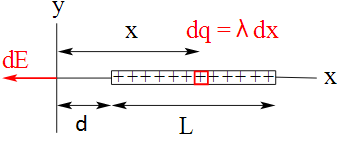 Charge per unit length, λ = Q/L
Charge per unit length, λ = Q/L
Charge of slice, dq = λ.dx
Thus, Electric potential due to uniformly charged rod: 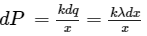
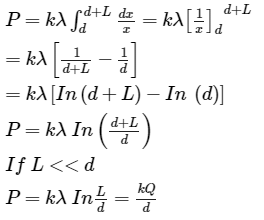
➤ Electric Potential Due to a Charged Ring
Let electric potential at point P due to small element of length dℓ be dV.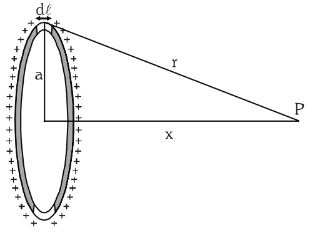
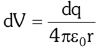 (distance between small element and point P is equal to r)
(distance between small element and point P is equal to r)
Thus, Electric potential due to whole ring: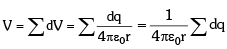
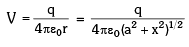
➤ Potential Due to a Uniformly Charged Disc
Find the electric potential at the axis of a uniformly charged disc and use potential to find the electric field at same point.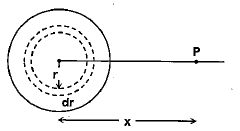 Thus, Electric Potential due to ring element of radius r and thickness dr is dv:
Thus, Electric Potential due to ring element of radius r and thickness dr is dv: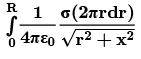
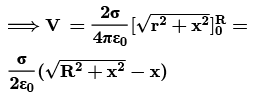
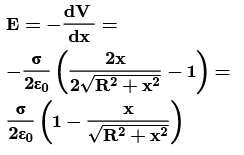
|
22 videos|163 docs|17 tests
|
















