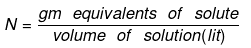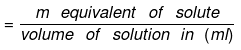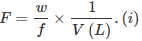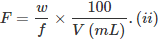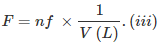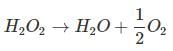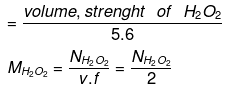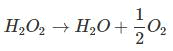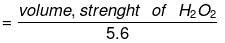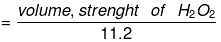Empirical Formulas
- The Empirical formulas express the simplest atomic ratio between the elements in the compound. Such formulas are called empirical formulas.
- An empirical formula does not necessarily represent the actual numbers of atoms present in a molecule of a compound it represents only the ratio between those numbers.
- So it may or may not represent the actual formula of the molecule. It can be deduced by knowing the weight % of all the constituent elements with their atomic masses for the given compound.
Example: C6H12O6, CH3COOH, HCHO
All have the same empirical formula CH2O, but they are different. Structure of Glucose
Structure of Glucose
The empirical formula of a compound can be determined by the following steps:
(i) Write the name of detected elements in the column 1 present in the compound. Write the corresponding atomic mass in column 2.
(ii) Write the experimentally determined percentage composition by weight of each element present in the compound in column 3.
(iii) Divide the percentage of each element by its atomic weight to get the relative number of atoms of each element in column 4.
(iv) Divide each number obtained for the respective elements in step (iii) by the smallest number among those numbers so as to get the simplest ratio in column 5.
(v) If any number obtained in step (iv) is not a whole number then multiply all the numbers by a suitable integer to get the whole-number ratio. This ratio will be the simplest ratio of the atoms of different elements present in the compound. The empirical formula of the compound can be written with the help of this ratio in column-6.
Example 1. A compound contains C = 71.23%, H = 12.95% and O = 15.81%. What is the empirical formula of the compound?
Solution.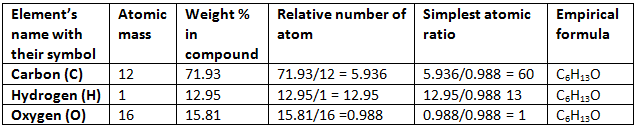
Example 2. The simplest formula of a compound containing 50% of element X (Atomic mass = 10) and 50% of the element Y (Atomic mass = 20) is:
(A) XY
(B) X2Y
(C) XY2
(D) X2Y3
Solution.
Hence (B) is correct.
Molecular Formulas
- The actual numbers of atoms of each element that occur in the smallest freely existing unit or molecule of the compound are expressed by the molecular formula of the compound.
- The molecular formula of a compound may be the empirical formula, or it may be a multiple of the empirical formula.
- Conclusively, the formula which represents the actual number of each individual atom in any molecule is known as the molecular formula.
- Molecular formula = (Empirical formula)n
Molecular weight = Empirical formula weight × n - If the vapour density of the substance is known, its molecular weight can be calculated by using the equation:
2 × Vapour density = Molecular weight - Example: The molecular formula of butene, C4H8, shows that each freely existing molecule of butene contains four atoms of carbon and eight atoms of hydrogen. Its empirical formula is CH2.
One molecule of ethylene (molecular formula C2H4) contains two atoms of carbon and four atoms of hydrogen. Its empirical formula is CH2. Both have the same empirical formula, yet they are different compounds with different molecular formulas.
Butene is C4H8 or four times the empirical formula, ethylene is C2H4 or twice the empirical formula. - For certain compounds, the molecular formula and the empirical formula may be the same.
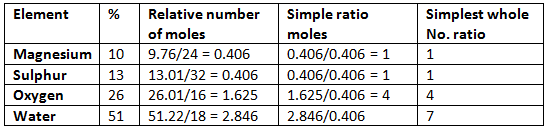
Example:
Hence the empirical formula is MgSO4.7H2O.
➢ For Writing Molecular Formula
- Determine empirical formula mass Add the atomic masses of various atoms present in the empirical formula.
- Divide Molar mass by empirical formula mass which will give the ‘n’ factor.
- Molecular formula = n × Empirical formula
Example 3. A compound contains 4.07 % hydrogen, 24.27 % carbon and 71.65 % chlorine. Its molar mass is 98.96 g. What are its empirical and molecular formulas?
Solution.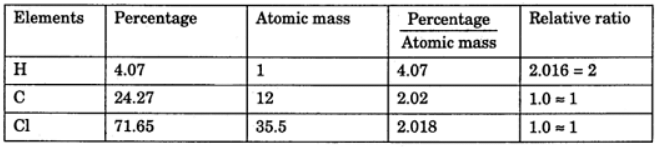
Empirical formula = CH2Cl
Molecular formula = n * Empirical formula
n = 98.96 / 48.5 = 2.04 = 2 (approx)
Molecular formula = 2 * CH2Cl = C2H4Cl2
Example 4. A compound of carbon, hydrogen and nitrogen contains these elements in the ratio 9:1:3.5. Calculate the empirical formula. If its molecular mass is 108, what is the molecular formula?
Solution.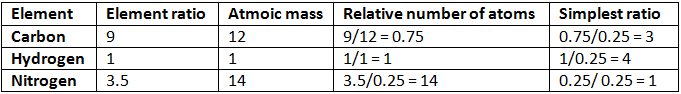
Empirical formula = C3H4N
Empirical formula mass = (3 × 12) + (4 × 1) + 14 = 54
n = mol. mass/Emp. mass
= 108/54 = 2
Thus, molecular formula of the compound = 2 × Empirical formula
= 2 × C3H4N
= C6H8N2
Example 5. 2.38 gm of uranium was heated strongly in a current of air. The resulting oxide weighed 2.806 g. Determine the empirical formula of the oxide. (At. mass U = 238; O = 16).
Solution.
Step 1: To calculate the percentage of uranium and oxygen in the oxide.
2.806 g of the oxide contain uranium = 2.38 g
∴ Percentage of uranium = 2.38/2.806 × 100 = 84.82
Hence, the percentage of oxygen in the oxide
= 100.00 – 84.82 = 15.18
Step 2: To calculate the empirical formula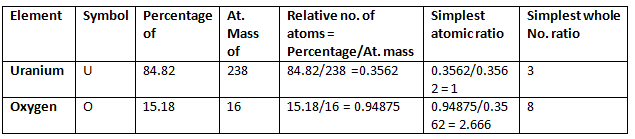
Hence, the empirical formula of the oxide is U3O8.
Example 6. Chemical analysis of a carbon compound gave the following percentage composition by weight of the elements present. Carbon 10.06%, hydrogen 0.84%, chlorine 89.10%. Calculate the empirical formula of the compound.
Solution.
Step 1: Percentage of the elements present.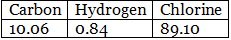
Step 2: Dividing the percentage compositions by the respective atomic weights of the elements.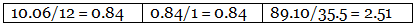
Step 3: Dividing each value in step 2 by the smallest number among them to get simple atomic ratio.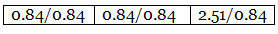
Step 4: Ratio of the atoms present in the molecule.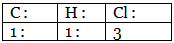
∴ The empirical formula of the compound C1H1Cl3 or CHCl3.
Example 7. A carbon compound on analysis gave the following percentage composition. Carbon 14.5%, hydrogen 1.8%, chlorine 64.46%, oxygen 19.24%. Calculate the empirical formula of the compound.
Solution.
Step 1: Percentage composition of the elements present in the compound.
Step 2: Dividing by the respective atomic weights.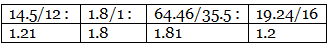
Step 3: Dividing the values in step 2 among them by the smallest number.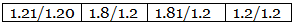
Step 4: Multiplication by a suitable integer to get the whole-number ratio.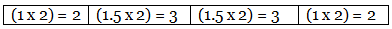
∴ The simplest ratio of the atoms of different elements in the compound.
C : H : Cl : O = 2 : 3 : 3 : 2
∴ The empirical formula of the compound C2H3Cl3O2.
Example 8. The empirical formula of a compound is CH2O. Its molecular weight is 90. Calculate the molecular formula of the compound. (Atomic weights C = 12, H = 1, O = 16)
Solution. Empirical formula = CH2O
Empirical formula weight = (12 + 2 + 16) = 30
n = molecular weight/empirical formula weight
∴ n = 90/30 = 3
The molecular formula (CH2O)3 = C3H6O3
Relation between the two:
Molecular formula= Empirical formula × n
Check out the importance of each step involved in calculations of the empirical formula.
➢ Density
(a) Absolute density
(b) Relative density
Absolute density = Mass/volume
Relative density = density of substance/density of a standard substance
Specific gravity = density of substance/density of H2O at 4oC
Vapour density: It is defined only for gas.
It is a density of gas with respect to H2 gas at the same temp & pressure.
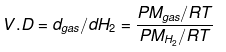
V.D = Mgas / MH2
V.D = M/2
V.D = Molecular wt of gas/Molecular wt of H2 gas
The density of Cl2 gas with respect to O2 gas = Molecular wt. of Cl2 gas/Molecular wt. of O2 gas
Try Yourself!
Q.1. A crystalline hydrated salt, on being rendered anhydrous, loses 45.6% of its mass. The percentage composition of the anhydrous salt is: Al = 10.5%, K = 15.1%, S =24.8% and oxygen = 49.6%. Find the empirical formula of the anhydrous and crystalline hydrated salt. [K = 39; Al = 27; S = 32; O = 16; H = 1]
Ans. The empirical formula of anhydrous salt = KAlS2O8
Hydrated salt composition: % anhydrous part = 54.4% and % H2O = 45.6%
The empirical formula of hydrated salt = KAIS2O8.12H2O
Q.2. A colorless crystalline compound has the following percentage composition: Sulphur 24.24%, nitrogen 21.21%, hydrogen 6.06% and the rest is oxygen. Determine the empirical formula of the compound. If the molecular mass is 132, what is the molecular formula of the compound? Name the compound if it is found to be sulphite.
Ans. Empirical formula SN2H8O4
Molecular formula = SN2H8O4
Name- Ammonium sulphite: (NH4)2SO3
Q.3. A gaseous hydrocarbon contains 85.7% carbon and 14.3% hydrogen. 1 litre of the hydrocarbon weighs 1.26 g at NTP. Determine the molecular formula of the hydrocarbon.
Ans. C2H4
Molarity and Molality
➢
Concentration of Solution
The concentration of a solution can be expressed in any of the following ways:
(a) % by Weight: Amount of solute dissolved in 100 gm of solution.
4.9% H2SO4 by weight: 100 gm of solution contains 4.9 gm of H2SO4.
(b) % by Volume: Volume of solute dissolved in 100 ml of solution.
x% H2SO4 by volume: 100 ml of solution contains x ml H2SO4
(c) % Weight by Volume: Weight of solute present in 100 ml of solution.
(d) % Volume by Weight: Volume of solute present in 100 gm of solution.
➢
Concentration Terms
➢
- Molarity (M): No. of moles of solute present in 1000 ml of solution.
Molarity (M) = moles of solute/volume of solution (lit)
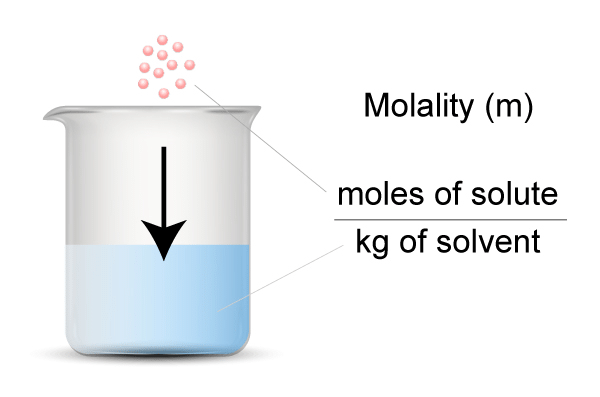
M = m.moles of solute/volume of solution (ml) - Molality (m): No. of moles of solute present in 1000 gm of solvent.
m = moles of solute/wt. of solvent in kg
m = m.moles of solute/wt. of solvent in gm
- Normality (N): No of gm. equivalents of solute present in 1000 ml of solution.


Number of gram equivalent of solute = Mass of solute in gram/equivalent weight of solute - Equivalent weight of solute (E) = Molar mass of solute / Valence factor
(i) Valence factor for base = acidity of base
(ii) Valence factor for acid = basicity of acid
(iii) Valence factor for element = valency
Thus, if one gram equivalent of a solute is present in one liter of the solution, the concentration of the solution is said to be one normal.
The relationship between Normality and Molarity can be expressed as:
► Molarity × Molecular mass = Strength of solution (g/L)
► Normality × Equivalent mass = Normality of the solution (g/L)
► Molarity × Molecular mass = Normality × Equivalent mass
Normality = n × Molarity
- Formality (f): It is the number of formula mass in grams present per litre of solution. In case formula mass is equal to molecular mass, formality is equal to molarity. Like molarity and normality, the formality is also dependent on temperature. It is used for ionic compounds in which there is no existence of a molecule. The mole of ionic compounds is called formole and molarity as formality.



Where,
w = weight of solute,
f = formula weight of solute
V = volume of solution
nf = no. of gram formula weight
- Mole Fraction: The mole fraction of a particular component in a solution is defined as the number of moles of that component per mole of solution. If a solution has nA mole of A & nB mole of B.

And, XA + XB = 1 - Parts per million (ppm):

- Volume strength of H2O2: The strength of H2O2 is represented as 10V, 20V, 30V etc.
20V H2O2 means one litre of this sample of H2O2 on decomposition gives 20 lit. of O2 gas at S.T.P.
Decomposition of H2O2 is given as:
1 mole = 1/2 × 22.4 lt O2 at S.T.P.
⇒ 34 g = 11.2 lt O2 at S.T.P.
To obtain 11.2 litre O2 at S.T.P., at least 34 gm H2O2 must be decomposed, and for 20 lt O2, we should decompose at least 34/112 × 20 gm H2O2.
1 lt solution of H2O2 contains 34/112 × 20 gm H2O2
1 lt solution of H2O2 contains 34/112 × 20/17 equivalents of H2O2
(E H2O2 = M/2 = 34/2 = 17)
Normality of H2O2 = 34/112 × 20/17
Normality of H2O2 (N)
Another Method:
From law of equivalence we have:
gm eq. of O2 = gm eq. of H2O2
gm eq. of O2 = moles × n factor of O2, = 20/22.4 x 4 = 20/5.6
gm. eq. of H2O2 = 20/5.6
and the volume of H2O2 is 1 lit.
this means 1 lit of H2O2 has 20/5.6 gm eq.
i.e. Normality N = 20/5.6
Normality of H2O2
Molarity of H2O2 (M)
Strength (in g/l): Denoted by S.
Strength = molarity × mol. wt.
= molarity × 34
strength = Normality × Eq. weight.
= Normality × 17
► Strength of Oleum
Oleum is SO3 dissolved in 100% H2SO4. Sometimes, oleum is reported as more than 100% by weight, say y% (where y > 100). This means that (y - 100) grams of water, when added to 100 g of given oleum sample, will combine with all the free SO3 in the oleum to give 100% sulphuric acid.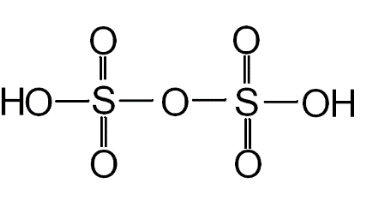 Structure of Oleum
Structure of Oleum
► Relationship between Molarity, Molality & density of Solution
Let the molarity of solution be 'M', molality be 'm' and the density of solution be d gm/m.
Molarity implies that there are M moles of solute in 1000 ml of solution.
wt. of solution = density × volume
= 1000 d gm wt of solute = MM1
where M1 is the molecular wt of solute.
wt of solvent = (1000 d - MM1) gm.
(1000 d - MM1) gm of solvent contains M moles of solute.
1000 gm of solvent have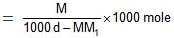
= Molality no. of moles of solute present in 1000 gm of solvent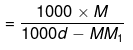
= Molality on simplifying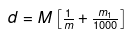
► Relationship between Molality & Mole Fraction
Consider a binary solution consisting of two components A (Solute) and B (Solvent).
Let xA & xB are the mole fraction of A & B respectively.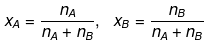
If molality of solution be m then
 =
= 
where MB is the molecular wt of the solvent B

Example 9. A bottle labeled with "12V H2O2" contains 700 ml solution. If a student mix 300 ml water in it what is the g/ liter strength & normality and volume strength of the final solution.
Solution. N = 12/5.6
Meq. of H2O2 = 12/5.6 x 100
let the normality of H2O2 on dilution be N.
Meq. before dilution = Meq. after dilution
N × 1000 = 12/5.6 x 100 N = 12/5.6 × 7/10 = 1.5 M = 1.5/2
strength gm/lit = 1.5/2 x 34 = 25.5
volume strength = N × 5.6 = 8.4 V
Example 10. Calculate the percentage of free SO3 in oleum (considered as a solution of SO3 in H2SO4) that is labeled '109% H2SO4 '.
Solution. '109% H2SO4' refers to the total mass of pure H2SO4, i.e., 109 g that will be formed when 100 g of oleum is diluted by 9 g of H2O which (H2O) combines with all the free SO3 present in oleum to form H2SO4.
H2O + SO3 → H2SO4
1 mole of H2O combines with 1 mole of SO3
or 18 g of H2O combines with 80 g of SO3
or 9 g of H2O combines with 40 g of SO3.
Thus, 100 g of oleum contains 40 g of SO3 or oleum contains 40% of free SO3.
Example 11. A 62% by mass of an aqueous solution of an acid has a specific gravity of 1.8. This solution is diluted such that the specific gravity of the solution became 1.2. Find the % by wt of acid in the new solution.
Solution. Density = 1.8
Volume of solution = Let x gm water be added in solution then
d = 0.6 x = 100
⇒ x = 166.67
Mass of new solution = 100 + 166.67 = 266.67
266.67 gm solution contains 62 gm of acid
% by mass = 23.24 %
Example 12. An aqueous solution is 1.33 molal in methanol. Determine the mole fraction of methanol & H2O.
Solution. 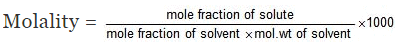
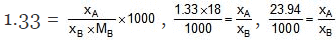
⇒ xA = 0.02394 xB, xA xB = 1
⇒ 1.02394 xB = 1
 = 0.98, xA = 0.02
= 0.98, xA = 0.02
Second Method: Let wt. of solvent = 1000 gm, molality = 1.33
= moles of solute
mole fraction of solute =  ,
, 
mole fraction of solute = 0.02
mole fraction of solvent = 1 - 0.02 = 0.98
Example 13. The density of 3 M solution of sodium thiosulphate (Na2S2O3) is 1.25 g/mL. Calculate
(i) amount of sodium thiosulphate
(ii) mole fraction of sodium thiosulphate
(iii) molality of Na and S2O32- ions
Solution.
(i) Let us consider one litre of sodium thiosulphate solution
wt. of the solution = density × volume (mL)
= 1.25 × 1000 = 1250 g.
wt. of Na2S2O3 present in 1 L of the solution
= molarity × mol. wt.
= 3 × 158 = 474 g.
wt. % of Na2S2O3 = 37.92%
(ii) Mass of 1 litre solution = 1.25 × 1000 g = 1250 g
[∵ density = 1.25 g/l]
Mole fraction of Na2S2O3 = Number of moles of Na2S2O3/Total number of moles
Moles of water = 1250 – 158 × 3/18 = 43.1
Mole fraction of Na2S2O3 = 3/3 + 43.1 = 0.065
(iii) 1 mole of sodium thiosulphate (Na2S2O3) yields 2 moles
of Na+ and 1 mole of S2O32-
Molality of Na2S2O3 = 3 × 1000/776 = 3.87
Molality of Na+ = 3.87 × 2 = 7.74 m
Molality of S2O2-3 = 3.87 m
FAQs on Empirical & Molecular Formula, Molarity and Molality - JEE
| 1. What is the difference between empirical formulas and molecular formulas? |  |
| 2. How can we determine the empirical formula of a compound? |  |
| 3. What is the significance of molarity and molality in chemistry? |  |
| 4. How is molarity calculated? |  |
| 5. What is the difference between molarity and molality? |  |

|
Explore Courses for JEE exam
|

|