Civil Engineering (CE) Exam > Civil Engineering (CE) Notes > Structural Analysis > Energy Methods
Energy Methods | Structural Analysis - Civil Engineering (CE) PDF Download
Strain Energy
The work done by the load in straining the body is stored within the strained material in the form of strain energy.
Strain energy,
U = 1 / 2 P(Al)
U = P2L / 2AE
Put
P = AEAℓ / L
Or
U = σ2 / 2E x V
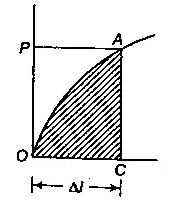 Strain Energy Diagram
Strain Energy Diagram
- Proof Resilience
The maximum strain energy that can be stored in a material is known as proof resilience.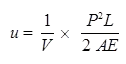
U = σ2/2E1
Where,
σ = p/A, u = 1/2 Ee2 - Strain energy of prismatic bar with varying sections:
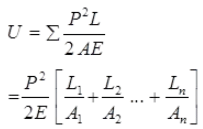
 Prismatic bar
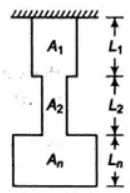
Prismatic bar - Strain energy of non-prismatic bar with varying axial force
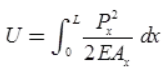 Ax = Cross-section of differential section.
Ax = Cross-section of differential section. Non-Prismatic Bar
Non-Prismatic Bar - Strain Energy in Torsion
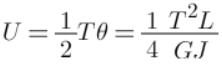
For solid shaft,
U = τ2/4G x Volume of Shaft
For hollow shaft,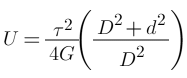 x Volume of Shaft
x Volume of Shaft
Castigliano’s First Theorem
It the strain energy of an elastic structure can be expressed as a function of generalized displacement, then the partial derivative of the strain energy with respect to generalized displacement gives the generalized force
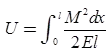
[Where M is function of W (load)]
Deflection: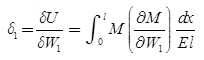
Slope: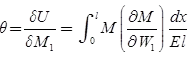
Theories of Failure
Theories of failure are defined as following groups.
- Maximum Principal Stress Theory (Rankine theory)
(i) According to this theory, permanent set takes place under a state of complex stress, when the value of maximum principal stress is equal to that of yield point stress as found in a simple tensile test.
(ii) For design, critical maximum principal stress (σ1) must not exceed the working stress (s1) for the material.
σ1 < σy
Note: For bittle material, it gives satisfactory result. Yield criteria for 3D stress system,
σ1 = σy or |σ3| = σry
Where, σy = Yield stress point in simple tension, and σy = Yield stress point in simple compression.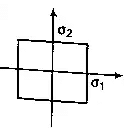 Stresses on rectangular Section
Stresses on rectangular Section - Maximum Principal Strain Theory (St. Venant’s theory):
According to this theory, a ductile material begins to yield when the maximum principal strain at which yielding occurs in simple tension.
For 3D stress system,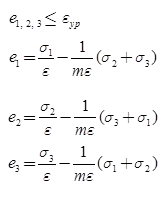
If ey = Yield point strain tensile σy/E
ery = Yield point strain compressive σry/E
According to theory, e1 = ey
Yield criteria: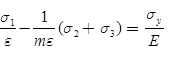
And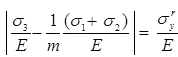
For 2D system,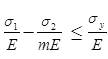
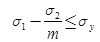
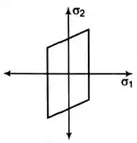 RhombusNote: This theory can estimate the elastic strength of ductile material.
RhombusNote: This theory can estimate the elastic strength of ductile material. - Maximum Shear Stress Theory (Guest & Tresca’s theory): According to this theory, failure of specimen subjected to any combination of loads when the maximum shearing stress at any point reaches the failure value equal to that developed at the yielding in an axial tensile or compressive test of the same material.
For 3D system:
Yielding criteria,
τmax = 1/2 (σ1 - σ3) = σy/2
In case of 2D: σ1 – σ3 = σy
Yielding criteria, σ1 - σ2 = σy
This theory gives well estimation for ductile material. - Maximum Strain Energy Theory (Haigh’s theory)
According to this theory, a body under complex stress fails when the total strain energy on the body is equal to the strain energy at elastic limit in simple tension. For 3D stress system yield criteria,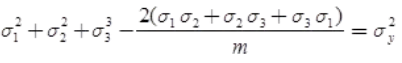
For 2D stress system,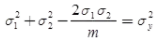
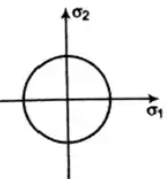 EllipseThis theory does not apply to brittle material for which elastic limit stress in tension and in compression are different.
EllipseThis theory does not apply to brittle material for which elastic limit stress in tension and in compression are different. - Maximum shear strain energy/Distortion energy theory/Mises-Henky theory
It states that inelastic action at any point in a body, under any combination of stress begins, when the strain energy of distortion per unit volume absorbed at the point is equal to the strain energy of distortion absorbed per unit volume at any point an a bar stressed to the elastic limit under the state of uniaxial stress as occurs in a simple tension/compression test.
1 / 2[(σ1 - σ2)2 + (σ1 - σ3)2 + (σ3 - σ1)2] ≤ σy2 For no failure
1 / 2[(σ1 - σ2)2 + (σ2 - σ3)2 + (σ3 - σ1)2] ≤ (σy / FOS)2 For no failure
The document Energy Methods | Structural Analysis - Civil Engineering (CE) is a part of the Civil Engineering (CE) Course Structural Analysis.
All you need of Civil Engineering (CE) at this link: Civil Engineering (CE)
|
34 videos|164 docs|31 tests
|
Related Searches
















