ICAI Notes- Equations and Matrices- 1 | Quantitative Aptitude for CA Foundation PDF Download
EQUATIONS
LEARNING OBJECTIVES
After studying this chapter, you will be able to:
- Understand the concept of equations and its various degrees – linear, simultaneous, quadratic and cubic equations;
- Know how to solve the different equations using different methods of solution; and
- Know how to apply equations in co-ordinate geometry.
2.1 INTRODUCTION
Equation is defined to be a mathematical statement of equality. If the equality is true for certain value of the variable involved, the equation is often called a conditional equation and equality sign ‘=’ is used; while if the equality is true for all values of the variable involved, the equation is called an identity.
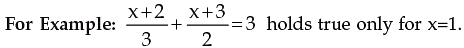
is an identity since it holds for all values of the variable x.
Determination of value of the variable which satisfies an equation is called solution of the equation or root of the equation. An equation in which highest power of the variable is 1 is called a Linear (or a simple) equation. This is also called the equation of degree 1. Two or more linear equations involving two or more variables are called Simultaneous Linear Equations. An equation of degree 2 (highest Power of the variable is 2) is called Quadratic equation and the equation of degree 3 is called Cubic Equation.
For Example: 8x+17(x–3) = 4 (4x–9) + 12 is a Linear equation
3x2 + 5x +6 = 0 is a quadratic equation.
4x3 + 3x2 + x–7 = 1 is a Cubic equation.
x+2y = 12x+3y = 2 are jointly called simultaneous equations.
2.2 SIMPLE EQUATION
A simple equation in one unknown x is in the form ax + b = 0.
Where a, b are known constants and a10
Note: A simple equation has only one root.
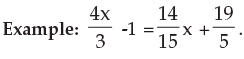
Solution: By transposing the variables in one side and the constants in other side we have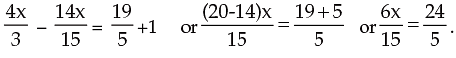

Illustrations:
1 . The denominator of a fraction exceeds the numerator by 5 and if 3 be added to both the
fraction becomes  Find the fraction
Find the fraction
Let x be the numerator and the fraction be  . By the question
. By the question  4x+12 = 3x+24 or x = 12
4x+12 = 3x+24 or x = 12
The required fraction is 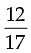
2. If thrice of A’s age 6 years ago be subtracted from twice his present age, the result would be equal to his present age. Find A’s present age.
Let x years be A’s present age. By the question
2x–3(x–6) = x
or 2x–3x+18 = x
or –x+18 = x
or 2x = 18
or x=9
∴ A’s present age is 9 years.
3. A number consists of two digits the digit in the ten’s place is twice the digit in the unit’s place. If 18 be subtracted from the number the digits are reversed. Find the number.
Let x be the digit in the unit’s place. So the digit in the ten’s place is 2x. Thus the number becomes 10(2x)+x. By the question
20x+x–18 = 10x + 2x
or 21x–18 = 12x
or 9x = 18
or x = 2
So the required number is 10 (2 × 2) + 2 = 42.
4. For a certain commodity the demand equation giving demand ‘d’ in kg, for a price ‘p’ in rupees per kg. is d = 100 (10 – p). The supply equation giving the supply s in kg. for a price p in rupees per kg. is s = 75(p - 3). The market price is such at which demand equals supply. Find the market price and quantity that will be bought and sold.
Given d = 100(10 – p) and s = 75(p – 3).
Since the market price is such that demand (d) = supply (s) we have
100 (10 – p) = 75 (p – 3) or 1000 – 100p = 75p – 225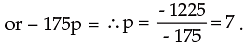
So market price of the commodity is Rs. 7 per kg.
∴ the required quantity bought = 100 (10 – 7) = 300 kg.
and the quantity sold = 75 (7 – 3) = 300 kg.
2.3 SIMULTANEOUS LINEAR EQUATIONS IN TWO UNKNOWNS
The general form of a linear equations in two unknowns x and y is ax + by + c = 0 where a b are non-zero coefficients and c is a constant. Two such equations a1x + b1y + c1 = 0 and a2 x + b2 x + c2 = 0 form a pair of simultaneous equations in x and y. A value for each unknown which satisfies simultaneously both the equations will give the roots of the equations.
2.4 METHOD OF SOLUTION
1. Elimination Method: In this method two given linear equations are reduced to a linear equation in one unknown by eliminating one of the unknowns and then solving for the other unknown.
Example 1: Solve: 2x + 5y = 9 and 3x – y = 5.
Solution: 2x + 5y = 9 …….. (i)
3x – y = 5 ………(ii)
By making (i) x 1, 2x + 5y = 9
and by making (ii) x 5, 15x – 5y = 25
__________________________________
Adding 17x = 34 or x = 2. Substituting this values of x in (i) i.e. 5y = 9 – 2x
we find,
5y = 9 – 4 = 5
∴y = 1
∴x = 2, y = 1.
2. Cross Multiplication Method: Let two equations be:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
We write the coefficients of x, y and constant terms and two more columns by repeating the coefficients of x and y as follows:
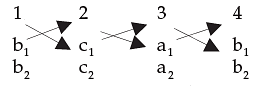
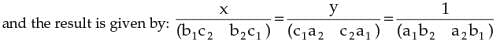
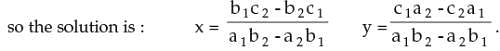

Example 2: 3x + 2y + 17 = 0
5x – 6y – 9 = 0
Solution: 3x + 2y + 17 = 0 ....... (i)
5x – 6y – 9 = 0 ........(ii)
Method of elimination: By (i) x3 we get 9x + 6y + 51 = 0 ...... (iii)
Adding (ii) & (iii) we get 14x + 42 = 0
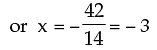
Putting x = –3 in (i) we get 3(–3) + 2y + 17 = 0
or, 2y + 8 = 0 or, y = 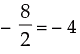
So x = –3 and y = –4
Method of cross-multiplication: 3x + 2y + 17 = 0
5x – 6y – 9 = 0
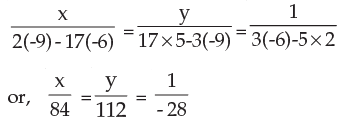

2.5 METHOD OF SOLVING SIMULTANEOUS LINEAR EQUATION WITH THREE VARIABLES
Example 1: Solve for x, y and z:
2x–y + z = 3 x + 3y – 2z = 11 3x – 2y + 4z = 1
Solution: (a) Method of elimination
2x – y + z = 3 .......(i)
x + 3y – 2z = 11 .... (ii)
3x – 2y + 4z = 1 .... (iii)
By (i) × 2 we get
4x – 2y + 2z = 6 …. (iv)
By (ii) + (iv), 5x + y = 17 ….(v) [the variable z is thus eliminated]x
By (ii) × 2, 2x + 6y – 4z = 22 ….(vi)
By (iii) + (vi), 5x + 4y = 23 ....(vii)
By (v) – (vii), –3y = – 6 or y = 2
Putting y = 2 in (v) 5x + 2 = 17, or 5x = 15 or, x = 3
Putting x = 3 and y = 2 in (i)
2 × 3 – 2 + z = 3
or 6–2+z = 3
or 4+z = 3
or z = –1
So x = 3, y = 2, z = –1 is the required solution.
(Any two of 3 equations can be chosen for elimination of one of the variables)
(b) Method of cross multiplication
We write the equations as follows:
2x – y + (z – 3) = 0
x + 3y + (–2z –11) = 0
By cross multiplication

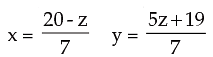
Substituting above values for x and y in equation (iii) i.e. 3x - 2y + yz = 1,
we have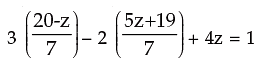
or 60–3z–10z–38 + 28z = 7
or 15z = 7–22 or 15z = –15 or z = –1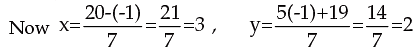
Thus x = 3, y = 2, z = –1
Example 2: Solve for x, y and z :


u+v+w = 5 ........ (i)
2u–3v–4w = –11........ (ii)
3u+2v–w = –6 ........ (iii)
By (i) + (iii) 4u+3v = –1 ........ (iv)
By (iii) x 4 12u+8v–4w = –24 ......... (v)
By (ii) – (v) –10u–11v = 13
or 10u + 11v = –13 .......... (vi)
By (iv) × 11 44x+33v = –11 …..…(vii)
By (vi) × 3 30u + 33v = –39 ……..(viii)
By (vii) – (viii) 14u = 28 or u = 2
Putting u = 2 in (iv) 4 × 2 + 3v = –1
or 8 + 3v = –1
or 3v = –9 or v = –3
Putting u = 2, v = –3 in (i) or 2–3 + w = 5
or –1 + w = 5 or w = 5+1 or w = 6
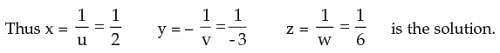
Example 3: Solve for x y and z:
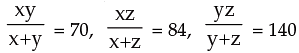
Solution: We can write as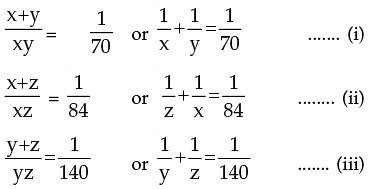
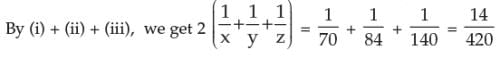
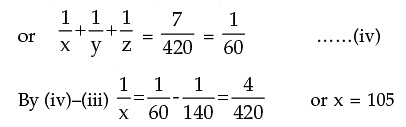

2.6 PROBLEMS LEADING TO SIMULTANEOUS EQUATIONS
Illustrations :
1. If the numerator of a fraction is increased by 2 and the denominator by 1 it becomes 1.
Again if the numerator is decreased by 4 and the denominator by 2 it becomes 1/2 . Find the fraction
Solution: Let x/y be the required fraction.

Thus x + 2 = y + 1 or x – y = –1 ......... (i)
and 2x – 8 = y–2 or 2x – y = 6 ......... (ii)
By (i) – (ii) –x = –7 or x = 7
from (i) 7–y = –1 or y = 8
So the required fraction is 7/8.
2. The age of a man is three times the sum of the ages of his two sons and 5 years hence his age will be double the sum of their ages. Find the present age of the man?
Solution: Let x years be the present age of the man and sum of the present ages of the two sons be y years.
By the condition x = 3y .......... (i)
and x + 5 = 2 ( y+5+5) ..........(ii)
From (i) & (ii) 3y + 5 = 2 (y+10)
or 3y + 5 = 2y + 20
or 3y – 2y = 20 – 5
or y = 15
∴ x = 3 × y = 3 × 15 = 45
Hence the present age of the main is 45 years
3. A number consist of three digit of which the middle one is zero and the sum of the other digits is 9. The number formed by interchanging the first and third digits is more than the original number by 297 find the number.
Solution: Let the number be 100x + y. we have x + y = 9……(i)
Also 100y + x = 100x + y + 297 …………………………….. (ii)
From (ii) 99(x – y) = –297
or x – y = –3 ….……………………………………………… (iii)
Adding (i) and (ii) 2x = 6 ∴ x = 3 ∴ from (i) y = 6
∴ Hence the number is 306.
2.7 QUADRATIC EQUATION
An equation of the form ax2 + bx + c = 0 where x is a variable and a, b, c are constants with a ≠ 0 is called a quadratic equation or equation of the second degree.
When b=0 the equation is called a pure quadratic equation; when b ¹ 0 the equation is called an adfected quadratic.
Examples: i) 2x2 + 3x + 5 = 0
ii) x2 – x = 0
iii) 5x2 – 6x –3 = 0
The value of the variable say x is called the root of the equation. A quadratic equation has got two roots.
How to find out the roots of a quadratic equation:
ax2 + bx +c = 0 (a ≠ 0)
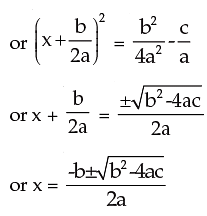
Let one root be and the other root be β
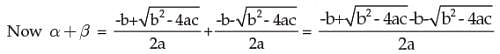
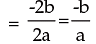
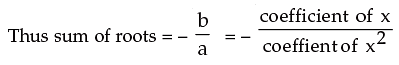
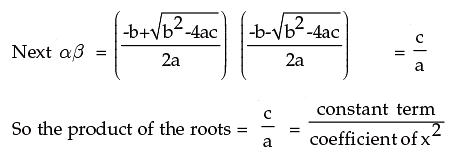
2.8 HOW TO CONSTRUCT A QUADRATIC EQUATION
For the equation ax2 + bx + c = 0 we have
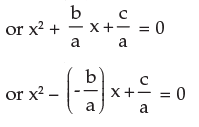
or x2 – (Sum of the roots) x + Product of the roots = 0
2.9 NATURE OF THE ROOTS
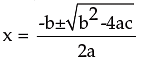
i) If b2>4ac = 0 the roots are real and equal;
ii) If b2>4ac >0 then the roots are real and unequal (or distinct);
iii) If b2>4ac <0 then the roots are imaginary;
iv) If b2>4ac is a perfect square ( ≠ 0) the roots are real, rational and unequal (distinct);
v) If b2>4ac > 0 but not a perfect square the rots are real, irrational and unequal.
Since b2 – 4ac discriminates the roots b2 – 4ac is called the discriminant in the equation ax2 + bx + c = 0 as it actually discriminates between the roots.
Note: (a) Irrational roots occur in pairs that is if  is a root then
is a root then 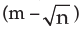 is the other root of the same equation.
is the other root of the same equation.
(b) If one root is reciprocal to the other root then their product is 1 and so  = 1 i.e. c = a
= 1 i.e. c = a
(c) If one root is equal to other root but opposite in sign then. their sum = 0 and so 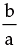 = 0. i.e. b = 0.
= 0. i.e. b = 0.
Example 1 : Solve x2 – 5x + 6 = 0
Solution: 1st method : x2 – 5x + 6 = 0
or x2 –2x –3x +6 = 0
or x(x–2) – 3(x–2) = 0
or (x–2) (x–3) = 0
or x = 2 or 3
2nd method (By formula) x2 – 5x + 6 = 0
Here a = 1 b = –5 c = 6 (comparing the equation with ax2 + bx+c = 0)
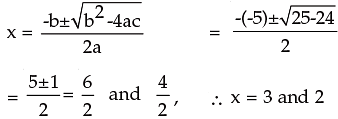
Example 2: Examine the nature of the roots of the following equations.
i) x2 – 8x2 + 16 = 0
ii) 3x2 – 8x + 4 = 0
iii) 5x2 – 4x + 2 = 0
iv) 2x2 – 6x – 3 = 0
Solution: (i) a = 1 b = –8 c = 16
b2 – 4ac = (–8)2 – 4.1.16 = 64 – 64 = 0
The roots are real and equal.
(ii) 3x2 – 8x + 4 = 0
a = 3 b = –8 c = 4
b2 – 4ac = (–8)2 – 4.3.4 = 64 – 48 = 16 > 0 and a perfect square
The roots are real, rational and unequal
iii) 5x2 – 4x + 2 = 0
b2 – 4ac = (–4)2 – 4.5.2 = 16–40 = –24 < 0
The roots are imaginary and unequal
(iv) 2x2 – 6x – 3 = 0
b2 – 4ac = (–6)2 – 4.2 (–3)
= 36 + 24 = 60 > 0
The root are real and unequal. Since b2 – 4ac is not a perfect square the roots are real irrational and unequal.
Illustrations:
1. If α and ß be the roots of x2 + 7x + 12 = 0 find the equation whose roots are ( α + ß )2 and (α - ß)2.
Solution : Now sum of the roots of the required equation
= (α + b)2 + (α + b)2 = (-7)2 + (α + b)2 - 4 ∝ b
= 49 + (–7)2 – 4x12 = 49 + 49 – 48 = 50
Product of the roots of the required equation = (α + b)2 (α - b)2 = 49 (49–48) = 49
Hence the required equation is x2 – (sum of the roots) x + product of the roots = 0
or x2 – 50x + 49 = 0
2. If a ,b be the roots of 2x2 – 4x – 1 = 0 find the value of 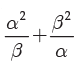
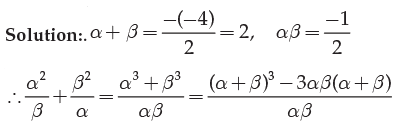

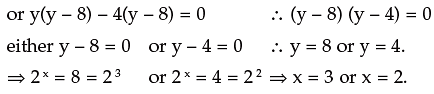
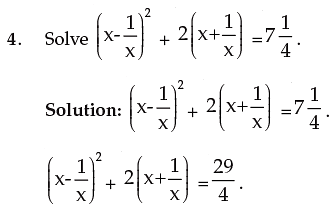

or 4p2 + 8p – 45 = 0
or 4p2 + 18p – 10p – 45 = 0
or 2p(2p + 9) – 5(2p + 9) = 0
or (2p – 5) (2p + 9) = 0.
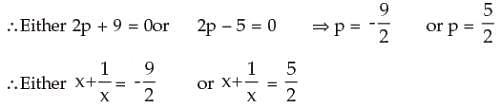
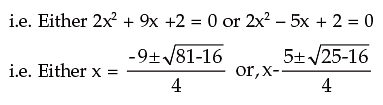
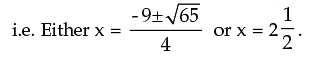
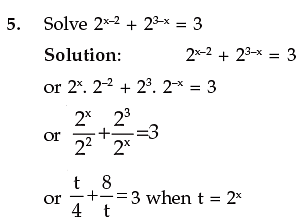
or t2 + 32 = 12t
or t2 – 12t + 32 = 0
or t2 – 8t – 4t + 32 = 0
or t(t–8) – 4(t–8) = 0
or (t–4) (t–8) = 0
∴ t = 48
For t = 4 2x = 4 = 22 i.e. x = 2
For t = 8 2x = 8 = 23 i.e. x = 3
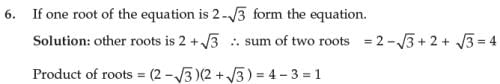
∴ Required equation is : x2 – (sum of roots)x + (product of roots) = 0 or x2 – 4x + 1 = 0.
7. If α β are the two roots of the equation x2 – px + q = 0 form the equation whose roots are 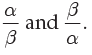
Solution: As α, β are the roots of the equation x2 – px + q = 0 α + β = – (– p) = p and α β = q.
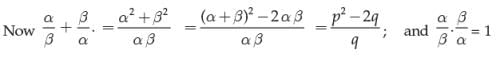

or qx2 – (p2 – 2q) x + q = 0
8. If the roots of the equation p(q – r)x2 + q(r – p)x + r(p – q) = 0
are equal show that 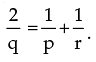
Solution: Since the roots of the given equation are equal the discriminant must be zero ie. q2(r – p)2 – 4. p(q – r) r(p – q) = 0
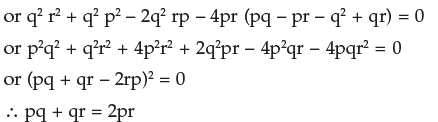
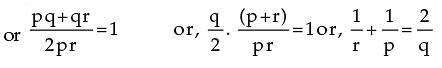
2.10 PROBLEMS ON QUADRATIC EQUATION
1. Difference between a number and its positive square root is 12; find the numbers?
Solution: Let the number be x.
Then 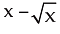 = 12 …………… (i)
= 12 …………… (i)

or (y – 4) (y + 3) = 0 ∴ Either y = 4 or y = – 3 i.e. Either  or
or 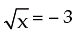
If  x = 9 if does not satisfy equation (i) so
x = 9 if does not satisfy equation (i) so 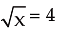 or x=16.
or x=16.
2. A piece of iron rod costs Rs. 60. If the rod was 2 metre shorter and each metre costs Re 1.00 more, the cost would remain unchanged. What is the length of the rod?
Solution: Let the length of the rod be x metres. The rate per meter is Rs. 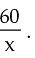
New Length = (x – 2); as the cost remain the same the new rate per meter is 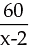
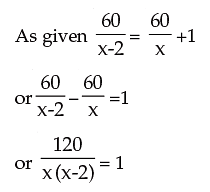
or x2 – 2x = 120 or x2 – 2x – 120 = 0 or (x – 12) (x + 10) = 0.
Either x = 12 or x = –10 (not possible) ∴ Hence the required length = 12m.
3. Divide 25 into two parts so that sum of their reciprocals is 1/6.
Solution: let the parts be x and 25 – x
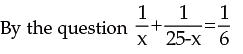
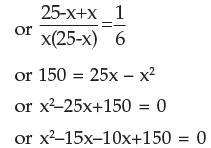
or x(x–15) – 10(x–15) = 0
or (x–15) (x–10) = 0
or x = 10, 15
So the parts of 25 are 10 and 15.
2.11 SOLUTION OF CUBIC EQUATION
On trial basis putting some value of x to check whether LHS is zero then to get a factor.
This is a trial and error method. With this factor to factorise the LHS and then to get values of x .
Illustrations :
1. Solve x3 – 7x + 6 = 0
Putting x = 1 L.H.S is Zero. So (x–1) is a factor of x3 – 7x + 6
We write x3–7x +6 = 0 in such a way that (x–1) becomes its factor. This can be achieved by writing the equation in the following form.
or x3–x2+x2–x–6x+6 = 0
or x2(x–1) + x(x–1) – 6(x–1) = 0
or (x–1)(x2+x–6) = 0
or (x–1)(x2+3x–2x–6) = 0
or (x–1){x(x+3) – 2(x+3) } = 0
or (x–1)(x–2)(x+3) = 0
2. Solve for real x: x3 + x + 2 = 0
Solution: By trial we find that x = –1 makes the LHS zero. So (x + 1) is a factor of x3 + x + 2
We write x3 + x + 2 = 0 as x3 + x2 – x2 – x + 2x + 2 = 0
or x2(x + 1) – x(x + 1) + 2(x + 1) = 0
or (x + 1) (x2 – x + 2) = 0.
Either x + 1 = 0
or x2 – x + 2 = 0 i.e. x = –1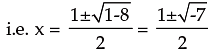
As x = 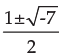 is not real, x = –1 is the required solution.
is not real, x = –1 is the required solution.
|
114 videos|164 docs|98 tests
|
FAQs on ICAI Notes- Equations and Matrices- 1 - Quantitative Aptitude for CA Foundation
| 1. What are equations and matrices? |  |
| 2. How are equations and matrices used in the CA Foundation exam? |  |
| 3. What are the key properties of equations and matrices? |  |
| 4. Can you provide an example of solving an equation using matrices? |  |
| 5. How can I excel in solving equations and matrices for the CA Foundation exam? |  |
|
114 videos|164 docs|98 tests
|

|
Explore Courses for CA Foundation exam
|

|


















