Equivalent Resistance | Network Theory (Electric Circuits) - Electrical Engineering (EE) PDF Download
The equivalent resistance is a term used to describe the total resistance in a series or parallel circuit, whether you're looking at the whole circuit or just a section of it. It's basically the total resistance measured between two points or nodes in the network. While it might sound a bit complex, it's essentially another way of saying "total resistance."
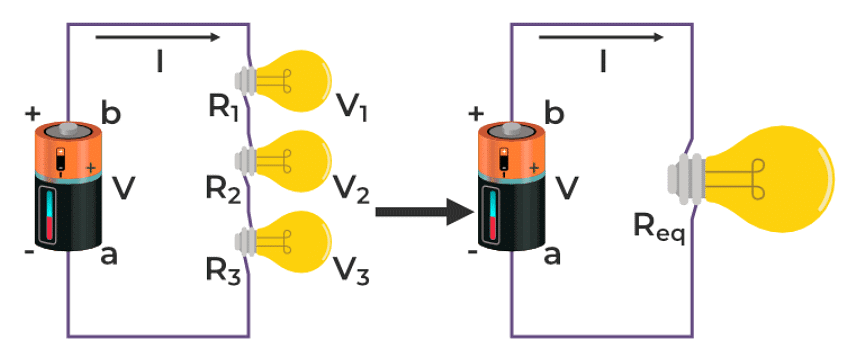 R1 + R2 + R3 = Req
R1 + R2 + R3 = Req
Understanding Equivalent Resistance in Electrical Circuits
- Imagine you have a complicated network of electrical components, like resistors. Well, you can replace that whole network with a single resistor. When you do this, you'll still get the same result when you apply voltage or current to it. It's like using the network itself.
Before we discuss what equivalent resistance is, we can describe resistance. Resistance is a measure of how much a device or material can resist the movement of electricity through it. It is inversely related to current, higher resistance means reduced current flow; reduced resistance means higher current flow.
How to find Equivalent Resistance?
- The equivalent resistance represents the total effect of all resistors in the circuit. The equivalent resistance can be measured in either a series or parallel circuit.
- Resistor comprises two junctions with which the current passes in and out of it. They are passive devices that utilize electricity.
- In order to improve the net resistance, the resistors must be wired in series and the resistors must be connected in parallel to reduce the resistance.
Equivalent Resistance: Parallel Circuit
A parallel circuit is one in which elements are connected to different branches. In a parallel circuit, the voltage drop is the same for each parallel branch. The total current in each branch is equal to the current outside the branches.
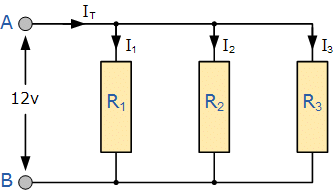 Parallel Circuit
Parallel Circuit
The equivalent resistance of the circuit is the amount of resistance that a single resistor will require in order to equalise the total effect of the set of resistors present in the circuit. For parallel circuits, the equivalent resistance of a parallel circuit is given as:
where R1, R2, and R3 are the resistance values of the individual resistors that are connected in parallel.
The total amount of current will often vary inversely with the level of cumulative resistance. There is a direct relation between the resistance of the individual resistors and the total resistance of the resistance collection.
If all endpoints of the resistors are wired to both endpoints of the power supply, so the resistors are connected in parallel and their equivalent resistance declines between their endpoints. There is more than one direction to flow in parallel circuit current.
To investigate this relationship, let’s start with the simplest case of two resistors positioned in parallel branches, each of which has the same resistance value as 4Ω. Since the circuit provides two equivalent paths for the charge transport, just one-half of the charge can choose to travel through the branch.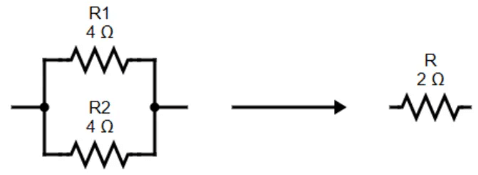 Although each branch gives 4Ω of resistance to any charge flowing through it, only one-half of all the charge flowing through the circuit may meet 4Ω of resistance of that branch. Thus, the presence of two 4Ω resistors in parallel will be equal to one 2Ω resistor in the circuit. This is the concept of equivalent resistance in a parallel circuit.
Although each branch gives 4Ω of resistance to any charge flowing through it, only one-half of all the charge flowing through the circuit may meet 4Ω of resistance of that branch. Thus, the presence of two 4Ω resistors in parallel will be equal to one 2Ω resistor in the circuit. This is the concept of equivalent resistance in a parallel circuit.
Equivalent Resistance: Series Circuit
If all components are connected in series, the circuit is referred to as a series circuit.
In a series circuit, each unit is connected in such a way that there is only one route through which the charge can travel through the external circuit.
Every charge traveling through the external circuit loop would travel through each resistor in a sequential manner. In a series circuit, the current has only one path to flow.
Charge flows together over the external circuit at a rate that is the same everywhere. The current is not stronger at one place and weaker at another point. Inversely, the exact amount of current varies with the total resistance. There is a direct relationship between the resistance of the single resistors and the total resistance of all the resistors present in the circuit.
For example, when two 6-Ω resistors are connected in series, it would be equivalent to having one 12-Ω resistor in the circuit. This is the concept of equivalent resistance in a series circuit.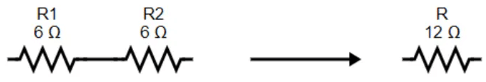 For series circuits, the equivalent resistance of a series circuit is given as
For series circuits, the equivalent resistance of a series circuit is given as
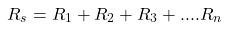 If the endpoint of one resistor is linearly connected to the endpoint of the neighboring resistor and the free end of one resistor and the free end of the other resistor are connected to the power supply. Then the two resistors are wired in series and their equal resistance increases between their endpoints.
If the endpoint of one resistor is linearly connected to the endpoint of the neighboring resistor and the free end of one resistor and the free end of the other resistor are connected to the power supply. Then the two resistors are wired in series and their equal resistance increases between their endpoints.
Equivalent Resistance Examples
For the Combination of Resistors Shown, Find the Equivalent Resistance Between Points A and B.
Example 1: For the given circuit below, what is the equivalent resistance between points A and B?
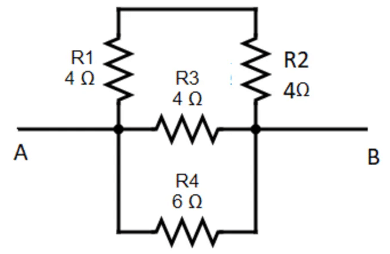
Sol: The two resistors R1 and R2 with value 4Ω are in series. So, their equivalent resistance value will be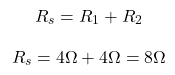
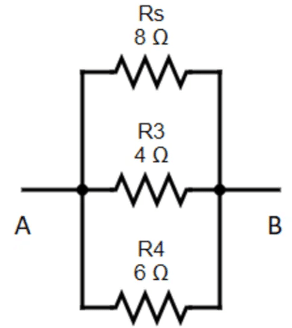
Rs , R3 and R4 are in parallel. The eqivalent resistance of the circuit.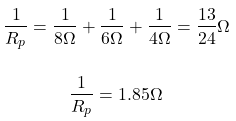
Example 2: For the given circuit below, calculate the equivalent resistance between the end points A and B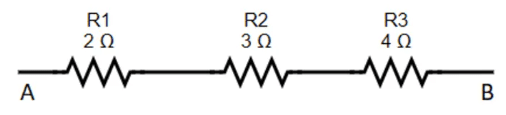
Sol: The expression for the equivalent resistance of the resistor connected in series is given as follows.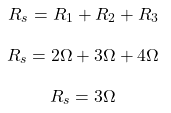
Which Circuit Has the Smallest Equivalent Resistance
Example: From the below given circuits, identify the circuit that has the smallest equivalent resistance.
A.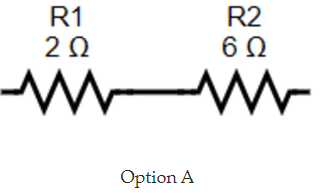
B.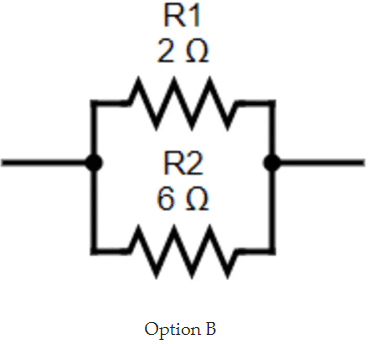
C.
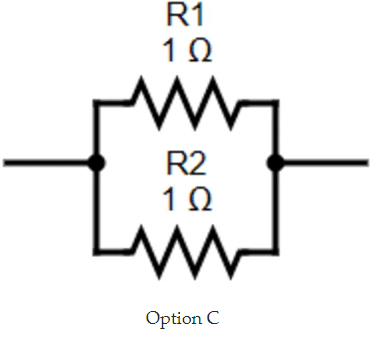
D.

Sol:
The first given is a series circuit. So, the equivalent resistance is given as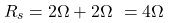
The second given is a parallel circuit. So, the equivalent resistance is given as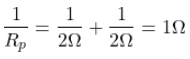
The second given is also a parallel circuit. So, the equivalent resistance is given as
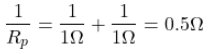
The fourth given is a series circuit. So, the equivalent resistance is given as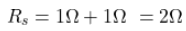
So, from the above calculation it is seen that the third option has the smallest euqivalent resistance value.
Difficult Equivalent Resistance Problems
Example 1: Find the Equivalent Resistance of the given circuit.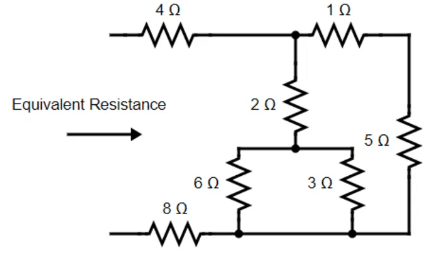
Sol:
To get the Equivalent Resistance we combine resistors in series and in parallel. Here, 6Ω and 3Ω are in parallel. So, the equivalent resistance is given as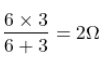
Also, the 1Ω and 5Ω resistors are in series. Hence the equivalent resistance will be given as,
1Ω + 5Ω = 6Ω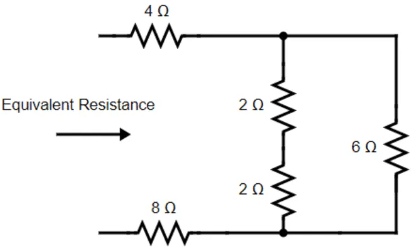
After reduction, we now notice, 2Ω and 2Ω are in series, so the equivalent resistance
2Ω+2Ω = 4Ω
This 4Ω resistor is now in parallel with the 6Ω resistor. So, their equivalent resistance will be given as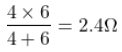
Now replacing the above circuit with appropriate values, the three resistors will be in series. So, the final equivalent resistance is given as Req = 4Ω + 2.4Ω + 8Ω = 14.4Ω
Req = 4Ω + 2.4Ω + 8Ω = 14.4Ω
Example 2: What is the equivalent resistance between points A and B?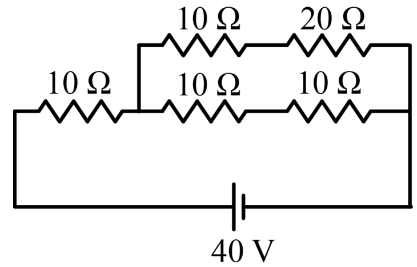
Sol:
To find the current through the battery we need to find the equivalent resistance of the circuit. The total current I is divided into I1 and I2. The current I1 passes through two 10Ω resistors as they are connected in series and have the same current. The current I2 passes through 10Ω and 20Ω resistors as they have the same current.
We need to find the current I2 by first calculating the current I that passes through the battery.
We see that 10Ω and 20Ω resistors are connected in series. We replace them with an equivalent resistor with a resistance of
Req = 10Ω + 20Ω = 30Ω
Two 10Ω resistors are connected in series. We replace them with an equivalent resistance of
Req = 10Ω + 10Ω = 20Ω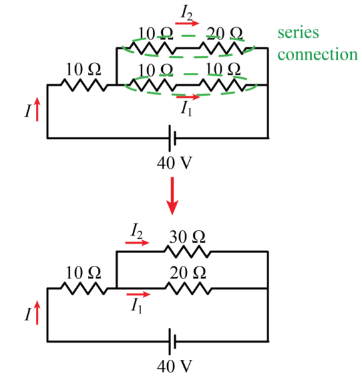 Now we have two resistors 30Ω and 20Ω connected in parallel. We can replace with an equivalent resistor.
Now we have two resistors 30Ω and 20Ω connected in parallel. We can replace with an equivalent resistor.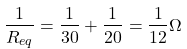
Finally, we have two resistors 10Ω and 12Ω connected in series. The equivalent resistance of these two resistors is
Req = 10Ω + 12Ω = 22Ω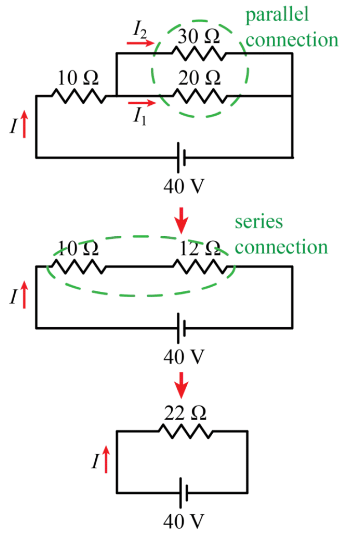
Let us try to understand How to find the current through the circuit,
We can find the current I through the battery. It is,
This current is divided between two currents I1 and I2. So, the total current
I= I1 + I2
1.8 = I1 + I2 ...(1)
The second equation, which relates the currents, is the condition that the voltage across the resistor 30Ω is equal to the voltage across the resistor 20Ω.
20 x I1 = 30 x I2 ...(2)
From the above equations ((1) and (2) the current I2 is found.
I1 = 1.8 - I2
Then we substitute this relation into equation (2),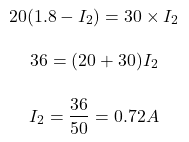
So, now the current I1 is given as
I1 = 1.8 - 0.72 = 1.08A
PYQs: Competitive Exams
Q: The equivalent resistance between the terminals A and B is ______ Ω. [2017]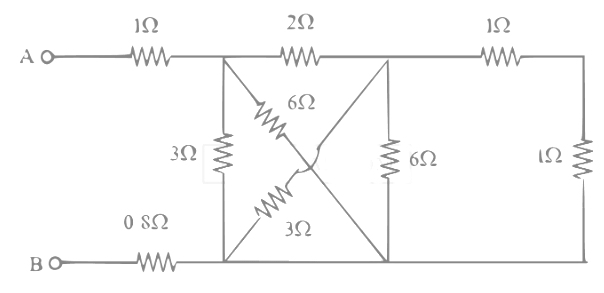
Ans: 3
Sol:
 The net resistance/equivalent resistance (R) of resistances in series is given by:
The net resistance/equivalent resistance (R) of resistances in series is given by:
Equivalent resistance, R = R1 + R2
When the terminals of two or more resistances are connected at the same two points and the potential difference across them is equal is called as resistances in parallel.
The net resistance/equivalent resistance(R) of resistances in parallel is given by:
We can redraw the given circuit as follows: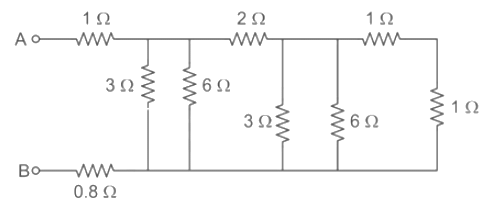
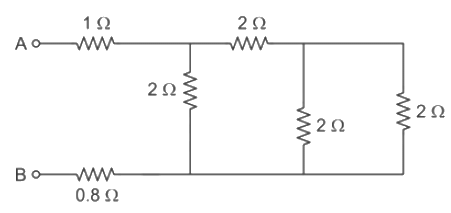
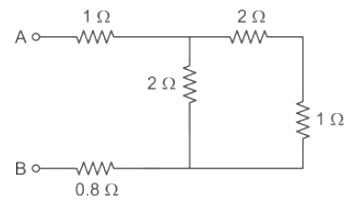
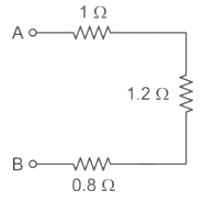
Hence, Answer becomes 3 Ω.
|
73 videos|139 docs|62 tests
|
FAQs on Equivalent Resistance - Network Theory (Electric Circuits) - Electrical Engineering (EE)
| 1. What is equivalent resistance in electrical circuits? |  |
| 2. How is equivalent resistance calculated in a parallel circuit? |  |
| 3. How is equivalent resistance calculated in a series circuit? |  |
| 4. Can you provide an example of equivalent resistance calculation in a series circuit? |  |
| 5. What are some common difficult equivalent resistance problems that students may encounter? |  |

















