Error Detection & Correction: Its Types | Computer Networks - Computer Science Engineering (CSE) PDF Download
Error Detection
For reliable communication, errors must be detected and corrected. For error detection, we are using many mechanisms.
Redundancy
One error detection mechanism is sending every data unit twice. The receiving device then would be able to do a bit-for-bit comparison between the two versions of the data. Any discrepancy would indicate an error, and an appropriate correction mechanism could be used. But instead of repeating the entire data stream, a shorter group of bits may be appended to the end of each unit. This technique is called redundancy because extra bits are redundant to the information. They are discarded as soon as the accuracy of the transmission has been determined.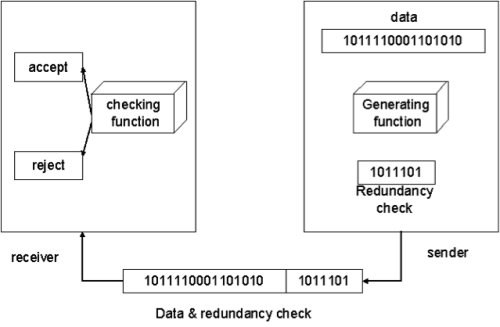
Types
Four types of redundancy checks are used in data communications. They are.
1. Vertical redundancy check (VRC)
2. Longitudinal redundancy check (LRC)
3. Cyclic redundancy check (CRC)
4. Checksum
Vertical Redundancy Check:
It is also known as a parity check. In this technique a redundant bit called a parity bit is appended to every data unit so that the total number of 1s in the unit, including the parity bit, becomes even for even parity or odd for odd parity.
In even parity, the data unit is passed through the even parity generator. It counts the number of 1s in the data unit. If odd number of 1s, then it sets 1 in the parity bit to make the number of 1s even. If the data unit has an even number of 1s, then it sets the parity bit to maintain the number of 1s as even. When it reaches its destination, the receiver puts all bits through an even parity checking function. If it counts an even number of 1s, then there is no error. Otherwise, there is some error.
Example:
The data is : 01010110
The VRC check : 010101100
In odd parity, the data unit is passed through the odd parity generator. It counts the number of 1s in the data unit. If there is an even number of 1s, then it sets 1 in the parity bit to make the number of 1s odd. If the data unit has an odd number of 1s, then it sets the parity bit to maintain the number of 1s as odd. When it reaches its destination, the receiver puts all bits through an odd parity checking function. If it counts an odd number of 1s, then there is no error. Otherwise, there is some error.
Example
The data is: 01010110
The VRC check: 01010111
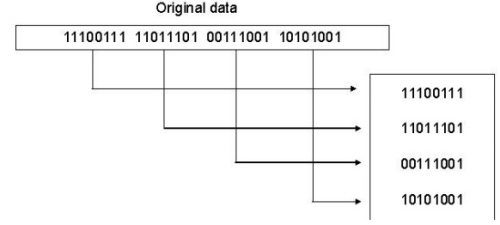
Longitudinal Redundancy Check
In this, a block of bits is organized in a table (rows and columns). For example, instead of sending a block of 32 bits, we organize them in a table made of four rows and eight columns. We then calculate the parity bit for each column and create a new row of eight bits, which are the parity bits for the whole block
Cyclic Redundancy Check
CRC is based on binary division. In this, a sequence of redundant bits, called a CRC remainder, is appended to the end of a data unit so that the resulting data unit becomes exactly divisible by a second predetermined binary number. At its destination, the incoming data unit is divided by the same number. If at this step there is no reminder, the data unit is assumed to be intact and therefore accepted. A remainder indicates that the data unit has been changed in transit and therefore must be rejected.
Here, the remainder is the CRC. It must have exactly one less bit than the divisor, and appending it to the end of the data string must make the resulting bit sequence exactly divisible by the divisor.
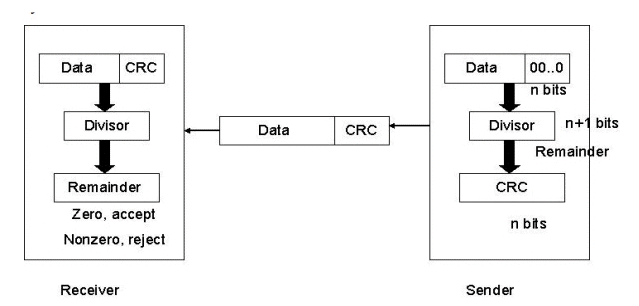
First, a string of n-1 0s is appended to the data unit. The number of 0s is one less than the number of bits in the divisor, which is n bits. Then the newly elongated data unit is divided by the divisor using a process called binary division. The remainder is CRC. The CRC is replaces the appended 0s at the end of the data unit.
The data unit arrives at the receiver first, followed by the CRC. The receiver treats the whole string as the data unit and divides it by the same divisor that was used to find the CRC remainder. If the remainder is 0, then the data unit is error-free. Otherwise, it has some error, and it must be discarded.
Checksum
The error detection method used by the higher layer protocols is called checksum. It consists of two parts. They are.
1. Checksum generator
2. Checksum checker
Checksum Generator:
In the sender, the checksum generator subdivides the data unit into equal segments of n bits. These segments are added with each other by using one's complement arithmetic in such a way that the total is also n bits long. That total is then complemented and appended to the end of the data unit.
Checksum Checker:
The receiver subdivides the data unit as above and adds all segments together and complements the result. If the extended data unit is intact, the total value found by adding the data segments and the checksum field should be zero. Otherwise, the packet contains an error, and the receiver rejects it.
Example
At the sender
Data unit: 10101001 00111001 10101001 00111001
Sum 1100010
Checksum 00011101
At the receiver
1) Received data: 10101001 00111001 00011101
10101001 00111001 00011101
Sum 11111111
Complement 00000000
It means that the pattern is ok.
2) Received data: 1010111 111001 00011101
10101111
11111001
00011101 Result 11000101 Carry 1 Sum 11000110 Complement 00111001
It means that the pattern is corrupted.
Error Correction
Error correction is handled in two ways. In one, when an error is discovered, the receiver can have the sender retransmit the entire data unit. In the other, a receiver can use an error-correcting code, which automatically corrects certain errors.
Types of error correction:
1. Single bit error correction2. Burst bit error correction
Single Bit Error Correction
To correct a single-bit error in an ASCII character, the error correction code must determine which of the seven bits has changed. In this case we have to determine eight different states: no error, error in position 1, error in position 2, error in position 3, error in position 4, error in position 5, error in position 6, and error in position 7. It looks like a three-bit redundancy code should be adequate because three bits can show eight different states. But what if an error occurs in the redundancy bits? Seven bits of data and three bits of redundancy equal 10 bits. So three bits are not adequate.To calculate the number of redundancy bits (r) required to correct a given number of data bits (m), we must find a relationship between m and r.
If the total number of bits in a transmittable unit is m+r, then r must be able to indicate at least m+r+1 different states. Of these, one state means no error, and m+r states indicate the location of an error in each of the m+r positions.
So the m+r+1 state must be discoverable by r bits. And r bits can indicate 2r different states. Therefore, 2r must be equal to or greater than m+r+1;
2r >= m+r+1
Hamming Code:
The Hamming Code can be applied to data units of any length and uses the relationship between data and redundancy bits.
Positions of redundancy bits in hamming code
The combinations used to calculate each of the four r values for a seven-bit data sequence are as follows:
r1: 1, 3, 5, 7, 9, 11
r2: 2, 3, 6, 7, 10, 11
r3: 4, 5, 6, 7
r4: 8, 9, 10, 11
Here, the r1 bit is calculated using all bit positions whose binary representation includes a 1 in the rightmost position (0001, 0011, 0101, 0111, 1001, and 1011). The r2 bit is calculated using all bit positions with a 1 in the second position (0010, 0011, 0110, 0111, 1010 and 1011); for r3, 1 at the third bit position (0100, 0101, 0110 and 0111); and for r4, 1 at the fourth bit position (1000, 1001, 1010 and 1011).
Calculating the r Values:
In the first step, we place each bit of the original character in its appropriate position in the 11-bit unit. Then, we calculate the even parities for the various bit combinations. The parity value of each combination is the value of the corresponding r bit. For example, r1 is calculated to provide even parity for a combination of bits 3, 5, 7, 9, and 11.
Error Detection and Correction:
Example:
At the sender:
Data to be sent: 1001101
Redundancy bit calculation:
Data sent with redundancy bits: 10011100101
At the receiver:
The receiver takes the transmission and recalculates four new r values using the same set of bits used by the sender plus the relevant parity (r) bit for each set. Then it assembles the new parity values into a binary number in order of r position (r8, r4, r2, r1).
Once the bit is identified, the receiver can reverse its value and correct the error.
Burst Bit Error Correction:
A Hamming Code can be designed to correct burst errors of a certain length. The number of redundancy bits required to make these corrections, however, is dramatically higher than that required for single-bit errors. To correct double-bit errors, for example, we must take into consideration that the two bits can be a combination of any two bits in the entire sequence. Three-bit correction means any three bits in the entire sequence and so on.
|
23 videos|171 docs|81 tests
|
FAQs on Error Detection & Correction: Its Types - Computer Networks - Computer Science Engineering (CSE)
| 1. What is error detection and correction in computer science engineering? |  |
| 2. What are the types of error detection and correction techniques? |  |
| 3. How does error detection and correction work? |  |
| 4. Why is error detection and correction important in computer science engineering? |  |
| 5. What are the advantages of forward error correction (FEC) in error detection and correction? |  |
















