Estimation of Preconsolidation Stress | Soil Mechanics - Civil Engineering (CE) PDF Download
Estimation of Preconsolidation Stress
It is possible to determine the preconsolidation stress that the soil had experienced. The soil sample is to be loaded in the laboratory so as to obtain the void ratio - effective stress relationship. Empirical procedures are used to estimate the preconsolidation stress, the most widely used being Casagrande's construction which is illustrated.

The steps in the construction are:
• Draw the graph using an appropriate scale.
• Determine the point of maximum curvature A.
• At A, draw a tangent AB to the curve.
• At A, draw a horizontal line AC.
• Draw the extension ED of the straight line portion of the curve.
• Where the line ED cuts the bisector AF of angle CAB, that point corresponds to the preconsolidation stress.
Analysis of Consolidation - Terzaghi's Theory
The total stress increases when additional vertical load is first applied. Instantaneously, the pore water pressure increases by exactly the same amount. Subsequently there will be flow from regions of higher excess pore pressure to regions of lower excess pore pressure causing dissipation. The effective stress will change and the soil will consolidate with time. This is shown schematically.

On the assumption that the excess pore water drains only along vertical lines, an analytical procedure can be developed for computing the rate of consolidation.
Consider a saturated soil element of sides dx, dy and dz.

The initial volume of soil element = dx.dy.dz
If n is the porosity, the volume of water in the element = n.dx.dy.dz
The continuity equation for one-dimensional flow in the vertical direction is

Only the excess head (h) causes consolidation, and it is related to the excess pore water pressure (u) by
h = u/gw.The Darcy equation can be written as

The Darcy eqn. can be substituted in the continuity eqn., and the porosity n can be expressed in terms of void ratio e, to obtain the flow equation as

The soil element can be represented schematically as

If e0 is the initial void ratio of the consolidating layer, the initial volume of solids in the element is (dx dy dz ) / (1 + e0), which remains constant. The change in water volume can be represented by small changes De in the current void ratio e.
The flow eqn. can then be written as

or

This is the hydrodynamic equation of one-dimensional consolidation.
If av = coefficient of compressibility, the change in void ratio can be expressed as De = av.(-Ds') = av.(Du) since any increase in effective stress equals the decrease in excess pore water pressure. Thus,

The flow eqn. can then be expressed as

By introducing a parameter called the coefficient of consolidation,  the flow eqn. then becomes
the flow eqn. then becomes

This is Terzaghi's one-dimensional consolidation equation. A solution of this for a set of boundary conditions will describe how the excess pore water pressure u dissipates with time t and location z. When all the u has dissipated completely throughout the depth of the compressible soil layer, consolidation is complete and the transient flow situation ceases to exist.
Solution of Terzaghi's Theory
During the consolidation process, the following are assumed to be constant:
1. The total additional stress on the compressible soil layer is assumed to remain constant.
2. The coefficient of volume compressibility (mV) of the soil is assumed to be constant.
3. The coefficient of permeability (k) for vertical flow is assumed to be constant.
There are three variables in the consolidation equation:
1. the depth of the soil element in the layer (z)
2. the excess pore water pressure (u)
3. the time elapsed since application of the loading (t)

To take care of these three variables, three non-dimensional parameters are provided:
1. Drainage path ratio,  , where H = drainage path which is the longest path taken by the pore water to reach a permeable sub-surface layer above or below.
, where H = drainage path which is the longest path taken by the pore water to reach a permeable sub-surface layer above or below.
2. Consolidation ratio at depth z, Uz , which is the ratio of dissipated pore pressure to the initial excess pore pressure. This represents the stage of consolidation at a certain location in the compressible layer.
3. Time factor, 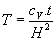
The graphical solution of Terzaghi's one-dimensional consolidation equation using the non-dimensional parameters is shown.

The figure is symmetrical about the horizontal line at 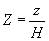 = 1.
= 1.
For double drainage conditions, pore water above this location flows upwards whereas water below this location flows downwards. Thus, the horizontal line at Z = 1 is equivalent to an imperious boundary. For single drainage conditions, only either the top half or bottom half of the figure is to be used, and the drainage path is equal to the thickness of the compressible layer.
The above graphical solution shows how consolidation proceeds with time at different locations for a particular set of boundary conditions, but it does not describe how much consolidation occurs as a whole in the entire compressible layer.
The variation of total consolidation with time is most conveniently plotted in the form of the average degree of consolidation (U) for the entire stratum versus dimensionless time T, and this is illustrated below.

There are useful approximations relating the degree of consolidation and the time factor, viz:
For U £ 0.60, T = ( p /4).U2
For U > 0.60, T = 1.781 – 0.933 log10(100 - U%)
Consolidation Settlement and Time
To estimate the amount of consolidation which would occur and the time it would take to occur, it is necessary to know:
- The boundary and drainage conditions
- The loading conditions
- The relevant parameters of the soil, including initial void ratio, coefficient of compressibility, coefficient of volume compressibility , compression index, and coefficient of consolidation. They are obtained from consolidation tests on representative undisturbed samples of the compressible soil stratum.

Comparing the compressible soil layer with a soil element of this layer,

De can be expressed in terms of av or Cc.

or

The magnitude of consolidation settlement is

or

Worked Examples
Example 1: A 3 m thick layer of saturated clay in the field under a surcharge loading will achieve 90% consolidation in 75 days in double drainage conditions. Find the coefficient of consolidation of the clay.

Solution:
As the clay layer has two-way drainage, H = 1.5 m = 150 cm
t90 = 75 days = 75 x 24 x 60 x 60 seconds
For 90% consolidation (U = 90%)
T90  = 0.848
= 0.848

Example 2: A 3 m thick clay layer in the field under a given surcharge will undergo 7 cm of total primary consolidation.If the first 4 cm of settlement takes 90 days, calculate the time required for the first 2 cm of settlement.
Solution:
Total consolidation = 7 cm
For 4 cm settlement, U1 = 4/7 x100 = 57.14%
For 2 cm settlement, U2 = 2/7 x 100 = 28.57%
t1 = 90 days.

Example 3: For a laboratory consolidation test on a soil specimen that is drained on both sides, the following were obtained:
Thickness of the clay specimen = 25 mm
P1 = 50 kN/m2 ; e1 = 0.92
P2 = 120 kN/m2 ;e2 = 0.78
Time for 50% consolidation = 2.5 min
Determine the soil permeability for the loading range.
Solution:

|
30 videos|76 docs|74 tests
|
FAQs on Estimation of Preconsolidation Stress - Soil Mechanics - Civil Engineering (CE)
| 1. What is preconsolidation stress in civil engineering? |  |
| 2. How is preconsolidation stress determined in practice? |  |
| 3. What factors can influence the preconsolidation stress of a soil? |  |
| 4. Why is preconsolidation stress important in civil engineering projects? |  |
| 5. How does preconsolidation stress affect soil consolidation? |  |

|
Explore Courses for Civil Engineering (CE) exam
|

|

















