Evaluation of Definite Integrals | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Definite Integration |

|
| Properties of definite integral |

|
| Improper Integrals |

|
| Solved Numericals |

|
Definite Integration
The integral 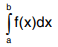 is called definite integral and is defined to be
is called definite integral and is defined to be 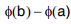 where ϕ(x) is the indefinite integral of ∫f(x)dx . It is read as integral from a to b of f(x), a is called the lower limit and b is called the upper limit.
where ϕ(x) is the indefinite integral of ∫f(x)dx . It is read as integral from a to b of f(x), a is called the lower limit and b is called the upper limit. 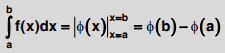 This is also called the theorem of calculus.
This is also called the theorem of calculus.
Properties of definite integral
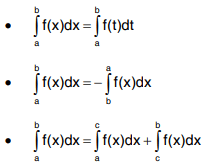
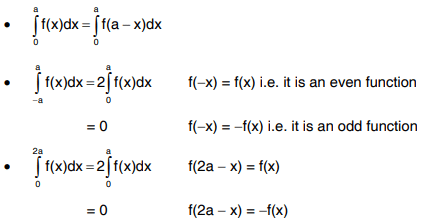
Improper Integrals
- The integral
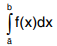 is said to be an improper integral of the first kind, if one or both the limits of integration are infinite.
is said to be an improper integral of the first kind, if one or both the limits of integration are infinite. - The integral
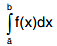 is said to be improper integral of second kind, if f(x) becomes unbounded at one or more points in the interval of integration [a, b].
is said to be improper integral of second kind, if f(x) becomes unbounded at one or more points in the interval of integration [a, b].
Limit comparison Test for Convergence and Divergence of Improper Integrals :
If f(x) and g(x) are positive functions and if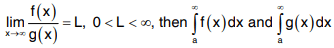 both converge or both diverge.
both converge or both diverge.
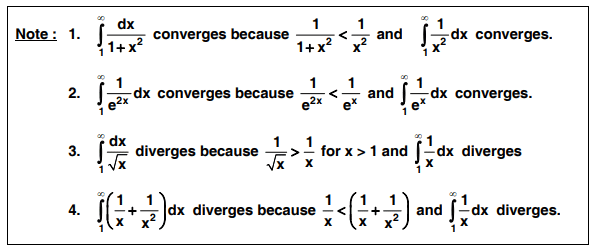
Solved Numericals
Q1. Integrate 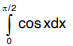 .
.
Solution: We know that ∫cosxdx = sinx + c
∴ 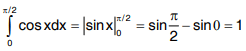
Q2. Integrate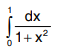 .
.
Solution: We know that
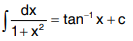
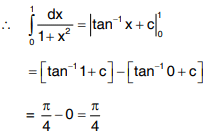
Q3. Evaluate 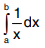 .
.
Solution: We know that 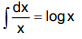
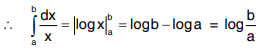
Q4. Evaluate 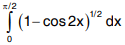 .
.
Solution: Let
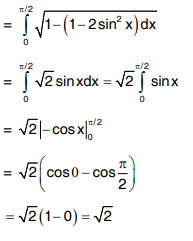
Q5. Solve 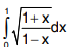 .
.
Solution: The integrand becomes infinite at x = 1.
The area under the curve 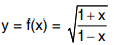 between the lines x = 0 and x = 1 is not well defined since the curve extends to infinity as x tends to 1 from the left. Nevertheless, we can define the area from x = 0 to x = t where 0 < t < 1.
between the lines x = 0 and x = 1 is not well defined since the curve extends to infinity as x tends to 1 from the left. Nevertheless, we can define the area from x = 0 to x = t where 0 < t < 1.
Then the integral 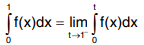
We also say that the improper integral converges.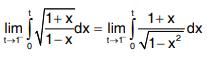
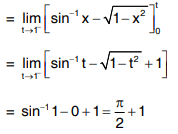
|
44 videos|109 docs|58 tests
|
FAQs on Evaluation of Definite Integrals - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What are the properties of definite integration? |  |
| 2. How do you evaluate definite integrals in mechanical engineering applications? |  |
| 3. What are improper integrals and how are they different from regular definite integrals? |  |
| 4. What are some common challenges faced when evaluating definite integrals in mechanical engineering? |  |
| 5. How can engineers effectively apply the concept of definite integration in real-world mechanical engineering scenarios? |  |




















