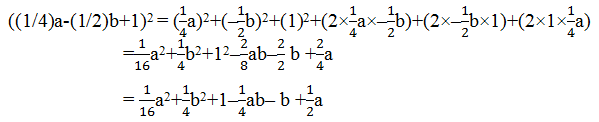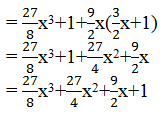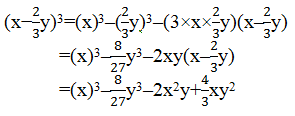NCERT Solutions for Class 9 Maths Chapter 2 - Polynomials (Exercise 2.4)
Q1: Use suitable identities to find the following products:
(i) (x + 4)(x + 10)
Ans: Using the identity (x + a)(x + b) = x2 + (a + b)x + ab,
[Here, a = 4 and b = 10]
We get,
(x + 4)(x + 10) = x2 + (4 + 10)x + (4 x 10)
= x2 + 14x + 40
(ii) (x + 8)(x – 10)
Ans: Using the identity, (x+a)(x+b) = x2+(a+b)x+ab
[Here, a = 8 and b = (–10)]
We get: (x + 8)(x – 10) = x2 + [8 + (–10)]x + [8 x (–10)]
= x2 + [8-10]x + [–80]
= x2 – 2x – 80
(iii) (3x + 4)(3x – 5)
Ans: Using the identity (x + a)(x + b) = x2 + (a + b)x + ab,
[Here, x = 3x, a = 4 and b = −5]
we get
(3x + 4)(3x – 5) = (3x)2 + [4 + (–5)]3x + [4 x (–5)]
= 9x2 + 3x(4–5)–20
= 9x2 – 3x – 20
(iv) (y2 + 3/2) (y2 - 3/2)
Ans: Using the identity (x + y)(x – y) = x2 – y2,
[Here, x = y2 and y = 3/2]
we get:
(y2+3/2)(y2–3/2) = (y2)2–(3/2)2
= y4–9/4
(v) (3 – 2x) (3 + 2x)
Ans: Using (a + b) (a - b) = a2 - b2,
putting a = 3 , b = 2x
= (3)2 - (2x)2
= 9 - 4x2
Q2: Evaluate the following products without multiplying directly:
(i) 103 × 107
Ans: (100+3) × (100+7)
Using identity, [(x+a)(x+b) = x2+(a+b)x+ab
Here, x = 100
a = 3
b = 7
We get, 103×107 = (100+3)×(100+7)
= (100)2+(3+7)100+(3×7))
= 10000+1000+21
= 11021
(ii) 95×96
Ans: (100-5)×(100-4)
Using identity, [(x-a)(x-b) = x2-(a+b)x+ab
Here, x = 100
a = -5
b = -4
We get, 95×96 = (100-5)×(100-4)
= (100)2+100(-5+(-4))+(-5×-4)
= 10000-900+20
= 9120
(iii) 104 × 96
Ans: (100+4)×(100–4)
Using identity, [(a+b)(a-b)= a2-b2]
Here, a = 100
b = 4
We get, 104×96 = (100+4)×(100–4)
= (100)2–(4)2
= 10000–16
= 9984
Q3: Factorise the following using appropriate identities:
(i) 9x2 + 6xy + y2
Ans: (3x)2+(2×3x×y)+y2
Using identity, x2+2xy+y2 = (x+y)2
Here, x = 3x
y = y
9x2+6xy+y2 = (3x)2+(2×3x×y)+y2
= (3x+y)2
= (3x+y)(3x+y)
(ii) 4y2 – 4y + 1
Ans: 4y2−4y+1 = (2y)2–(2×2y×1)+1
Using identity, x2 – 2xy + y2 = (x – y)2
Here, x = 2y
y = 1
4y2−4y+1 = (2y)2–(2×2y×1)+12
= (2y–1)2
= (2y–1)(2y–1)
(iii) x2– y2/100
Ans: x2–y2/100 = x2–(y/10)2
Using identity, x2-y2 = (x-y)(x+y)
Here, x = x
y = y/10
x2–y2/100 = x2–(y/10)2
= (x–y/10)(x+y/10)
Q4: Expand each of the following, using suitable identities:
(i) (x + 2y + 4z)2
Ans: Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = x
y = 2y
z = 4z
(x+2y+4z)2 = x22+(2y)2+(4z)2+(2×x×2y)+(2×2y×4z)+(2×4z×x)
= x2+4y2+16z2+4xy+16yz+8xz
(ii) (2x – y + z)2
Ans: Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = 2x
y = −y
z = z
(2x−y+z)2 = (2x)2+(−y)2+z2+(2×2x×−y)+(2×−y×z)+(2×z×2x)
= 4x2+y2+z2–4xy–2yz+4xz
(iii) (–2x + 3y + 2z)2
Ans: Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = −2x
y = 3y
z = 2z
(−2x+3y+2z)2 = (−2x)2+(3y)2+(2z)2+(2×−2x×3y)+(2×3y×2z)+(2×2z×−2x)
= 4x2+9y2+4z2–12xy+12yz–8xz
(iv) (3a – 7b – c)2
Ans: Using identity (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = 3a
y = – 7b
z = – c
(3a –7b– c)2 = (3a)2+(– 7b)2+(– c)2+(2×3a ×– 7b)+(2×– 7b ×– c)+(2×– c ×3a)
= 9a2 + 49b2 + c2– 42ab+14bc–6ca
(v) (–2x + 5y – 3z)2
Ans: Using identity, (x+y+z)2= x2+y2+z2+2xy+2yz+2zx
Here, x = –2x
y = 5y
z = – 3z
(–2x+5y–3z)2 = (–2x)2+(5y)2+(–3z)2+(2×–2x × 5y)+(2× 5y×– 3z)+(2×–3z ×–2x)
= 4x2+25y2 +9z2– 20xy–30yz+12zx
(vi) ((1/4)a-(1/2)b+1)2
Ans: Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = (1/4)a
y = (-1/2)b
z = 1
Q5: Factorise:
(i) 4x2 + 9y2 + 16z2 + 12xy – 24yz – 16xz
Ans: Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
We can say that, x2+y2+z2+2xy+2yz+2zx = (x+y+z)2
4x2+9y2+16z2+12xy–24yz–16xz = (2x)2+(3y)2+(−4z)2+(2×2x×3y)+(2×3y×−4z) +(2×−4z×2x)
= (2x+3y–4z)2
= (2x+3y–4z)(2x+3y–4z)
(ii) 2x2 + y2 + 8z2 – 2√2xy + 4√2 yz – 8xz
Ans: Using identity, (x +y+z)2 = x2+y2+z2+2xy+2yz+2zx
We can say that, x2+y2+z2+2xy+2yz+2zx = (x+y+z)2
2x2+y2+8z2–2√2xy+4√2yz–8xz
= (-√2x)2+(y)2+(2√2z)2+(2×-√2x×y)+(2×y×2√2z)+(2×2√2×−√2x)
= (−√2x+y+2√2z)2
= (−√2x+y+2√2z)(−√2x+y+2√2z)
Q6: Write the following cubes in expanded form:
(i) (2x + 1)3
Ans: Using identity,(x+y)3 = x3+y3+3xy(x+y)
(2x+1)3= (2x)3+13+(3×2x×1)(2x+1)
= 8x3+1+6x(2x+1)
= 8x3+12x2+6x+1
(ii) (2a – 3b)3
Ans: Using identity,(x–y)3 = x3–y3–3xy(x–y)
(2a−3b)3 = (2a)3−(3b)3–(3×2a×3b)(2a–3b)
= 8a3–27b3–18ab(2a–3b)
= 8a3–27b3–36a2b+54ab2
(iii) ((3/2)x+1)3
Ans: Using identity,(x+y)3 = x3+y3+3xy(x+y)
((3/2)x+1)3=((3/2)x)3+13+(3×(3/2)x×1)((3/2)x +1)
(iv) (x−(2/3)y)3
Ans: Using identity, (x –y)3 = x3–y3–3xy(x–y)
Q7: Evaluate the following using suitable identities:
(i) (99)3
Ans: We can write 99 as 100–1
Using identity, (x –y)3 = x3–y3–3xy(x–y)
(99)3 = (100–1)3
= (100)3–13–(3×100×1)(100–1)
= 1000000 –1–300(100 – 1)
= 1000000–1–30000+300
= 970299
= 970299
(ii) (102)3
Ans: We can write 102 as 100+2
Using identity,(x+y)3 = x3+y3+3xy(x+y)
(100+2)3 =(100)3+23+(3×100×2)(100+2)
= 1000000 + 8 + 600[100 + 2]
= 1000000 + 8 + 60000 + 1200
= 1061208
(iii) (998)3
Ans: We can write 99 as 1000–2
Using identity,(x–y)3 = x3–y3–3xy(x–y)
(998)3 =(1000–2)3
=(1000)3–23–(3×1000×2)(1000–2)
= 1000000000–8–6000(1000– 2)
= 1000000000–8- 6000000+12000
= 994011992
Q8: Factorise each of the following:
(i) 8a3 + b3 + 12a2b + 6ab2
Ans: The expression, 8a3+b3+12a2b+6ab2 can be written as (2a)3+b3+3(2a)2b+3(2a)(b)2
8a3+b3+12a2b+6ab2 = (2a)3+b3+3(2a)2b+3(2a)(b)2
= (2a+b)3
= (2a+b)(2a+b)(2a+b)
Here, the identity, (x +y)3 = x3+y3+3xy(x+y) is used.
(ii) 8a3 – b3 – 12a2b + 6ab2
Ans: The expression, 8a3–b3−12a2b+6ab2 can be written as (2a)3–b3–3(2a)2b+3(2a)(b)2
8a3–b3−12a2b+6ab2 = (2a)3–b3–3(2a)2b+3(2a)(b)2
= (2a–b)3
= (2a–b)(2a–b)(2a–b)
Here, the identity,(x–y)3 = x3–y3–3xy(x–y) is used.
(iii) 27 – 125a3 – 135a + 225a2
Ans: The expression, 27–125a3–135a +225a2 can be written as 33–(5a)3–3(3)2(5a)+3(3)(5a)2
27–125a3–135a+225a2 =
33–(5a)3–3(3)2(5a)+3(3)(5a)2
= (3–5a)3
= (3–5a)(3–5a)(3–5a)
Here, the identity, (x–y)3 = x3–y3-3xy(x–y) is used.
(iv) 64a3 – 27b3 – 144 a2b + 108 ab2
Ans: The expression, 64a3–27b3–144a2b+108ab2 can be written as
(4a)3–(3b)3 - 3(4a)2(3b)+3(4a)(3b)2
64a3–27b3 – 144a2b+108ab2
= (4a)3–(3b)3–3(4a)2(3b)+3(4a)(3b)2
=(4a–3b)3
=(4a–3b)(4a–3b)(4a–3b)
Here, the identity, (x – y)3 = x3 – y3 – 3xy(x – y) is used.
(v) 27p3– (1/216)−(9/2) p2+(1/4)p
Ans: The expression, 27p3–(1/216)−(9/2) p2+(1/4)p can be written as
(3p)3–(1/6)3−(9/2) p2+(1/4)p = (3p)3–(1/6)3−3(3p)(1/6)(3p – 1/6)
Using (x – y)3 = x3 – y3 – 3xy (x – y)
27p3–(1/216)−(9/2) p2+(1/4)p = (3p)3–(1/6)3−3(3p)(1/6)(3p – 1/6)
Taking x = 3p and y = 1/6
= (3p–1/6)3
= (3p–1/6)(3p–1/6)(3p–1/6)
Q9: Verify:
(i) x3+y3 = (x+y)(x2–xy+y2)
Ans: We know that, (x+y)3 = x3+y3+3xy(x+y)
⇒ x3+y3 = (x+y)3–3xy(x+y)
⇒ x3+y3 = (x+y)[(x+y)2–3xy]
Taking (x+y) common ⇒ x3+y3 = (x+y)[(x2+y2+2xy)–3xy]
⇒ x3+y3 = (x+y)(x2+y2–xy)
(ii) x3–y3 = (x–y)(x2+xy+y2)
Ans: We know that,(x–y)3 = x3–y3–3xy(x–y)
⇒ x3−y3 = (x–y)3+3xy(x–y)
⇒ x3−y3 = (x–y)[(x–y)2+3xy]
Taking (x+y) common ⇒ x3−y3 = (x–y)[(x2+y2–2xy)+3xy]
⇒ x3+y3 = (x–y)(x2+y2+xy)
Q10: Factorise each of the following:
(i) 27y3+125z3
Ans: The expression, 27y3+125z3 can be written as (3y)3+(5z)3
27y3+125z3 = (3y)3+(5z)3
We know that, x3+y3 = (x+y)(x2–xy+y2)
27y3+125z3 = (3y)3+(5z)3
= (3y+5z)[(3y)2–(3y)(5z)+(5z)2]
= (3y+5z)(9y2–15yz+25z2)
(ii) 64m3–343n3
Ans: The expression, 64m3–343n3can be written as (4m)3–(7n)3
64m3–343n3 = (4m)3–(7n)3
We know that, x3–y3 = (x–y)(x2+xy+y2)
64m3–343n3 = (4m)3–(7n)3
= (4m-7n)[(4m)2+(4m)(7n)+(7n)2]
= (4m-7n)(16m2+28mn+49n2)
Q11: Factorise 27x3 + y3 + z3 – 9xyz.
Solution: The expression27x3+y3+z3–9xyz can be written as (3x)3+y3+z3–3(3x)(y)(z)
27x3+y3+z3–9xyz = (3x)3+y3+z3–3(3x)(y)(z)
We know that, x3+y3+z3–3xyz = (x+y+z)(x2+y2+z2–xy –yz–zx)
27x3+y3+z3–9xyz = (3x)3+y3+z3–3(3x)(y)(z)
= (3x+y+z)[(3x)2+y2+z2–3xy–yz–3xz]
= (3x+y+z)(9x2+y2+z2–3xy–yz–3xz)
Q12: Verify that x3 + y3 + z3 – 3xyz = (1/2) (x + y + z)[(x – y)2 + (y – z)2 + (z – x)2]
Ans: We know that,
x3+y3+z3−3xyz = (x+y+z)(x2+y2+z2–xy–yz–xz)
⇒ x3+y3+z3–3xyz = (1/2)(x+y+z)[2(x2+y2+z2–xy–yz–xz)]
= (1/2)(x+y+z)(2x2+2y2+2z2–2xy–2yz–2xz)
= (1/2)(x+y+z)[(x2+y2−2xy)+(y2+z2–2yz)+(x2+z2–2xz)]
= (1/2)(x+y+z)[(x–y)2+(y–z)2+(z–x)2]
Q13: If x + y + z = 0, show that x3 + y3 + z3 = 3xyz.
Ans: We know that,
x3+y3+z3-3xyz = (x +y+z)(x2+y2+z2–xy–yz–xz)
Now, according to the question, let (x+y+z) = 0,
then, x3+y3+z3 -3xyz = (0)(x2+y2+z2–xy–yz–xz)
⇒ x3+y3+z3–3xyz = 0
⇒x3+y3+z3 = 3xyz
Hence Proved
Q14: Without actually calculating the cubes, find the value of each of the following:
(i) (–12)3 + (7)3 + (5)3
Ans: Let a = −12
b = 7
c = 5
We know that if x+y+z = 0, then x3+y3+z3=3xyz.
Here, −12+7+5=0
(−12)3+(7)3+(5)3 = 3xyz
= 3×-12×7×5
= -1260
(ii) (28)3 + (–15)3 + (–13)3
Ans: Let a = 28
b = −15
c = −13
We know that if x+y+z = 0, then x3+y3+z3 = 3xyz.
Here, x+y+z = 28–15–13 = 0
(28)3+(−15)3+(−13)3 = 3xyz
= 0+3(28)(−15)(−13)
= 16380
Q15: Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given:
(i) Area : 25a2–35a+12
Ans: Using the splitting the middle term method,
We have to find a number whose sum = -35 and product =25×12=300
We get -15 and -20 as the numbers [-15+-20=-35 and -15×-20=300]
25a2–35a+12 = 25a2–15a−20a+12
= 5a(5a–3)–4(5a–3)
= (5a–4)(5a–3)
Possible expression for length = 5a–4
Possible expression for breadth = 5a –3
(ii) Area : 35y2+13y–12
Ans: Using the splitting the middle term method,
We have to find a number whose sum = 13 and product = 35×-12 = 420
We get -15 and 28 as the numbers [-15+28 = 13 and -15×28=420]
35y2+13y–12 = 35y2–15y+28y–12
= 5y(7y–3)+4(7y–3)
= (5y+4)(7y–3)
Possible expression for length = (5y+4)
Possible expression for breadth = (7y–3)
Q16: What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
(i) Volume: 3x2–12x
Ans: 3x2–12x can be written as 3x(x–4) by taking 3x out of both the terms.
Possible expression for length = 3
Possible expression for breadth = x
Possible expression for height = (x–4)
(ii) Volume: 12ky2+8ky–20k
Ans: 12ky2+8ky–20k can be written as 4k(3y2+2y–5) by taking 4k out of both the terms.
12ky2+8ky–20k = 4k(3y2+2y–5)
[Here, 3y2+2y–5 can be written as 3y2+5y–3y–5 using splitting the middle term method.]
= 4k(3y2+5y–3y–5)
= 4k[y(3y+5)–1(3y+5)]
= 4k(3y+5)(y–1)
Possible expression for length = 4k
Possible expression for breadth = (3y +5)
Possible expression for height = (y -1)
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 2 - Polynomials (Exercise 2.4)
| 1. What are polynomials? |  |
| 2. How do you classify polynomials? |  |
| 3. What is the degree of a polynomial? |  |
| 4. How can we add or subtract polynomials? |  |
| 5. How can we multiply polynomials? |  |