NCERT Solutions for Class 10 Maths Chapter 5 - Arithmetic Progressions (Exercise 5.3) - 1
 Formula for Sum of an AP
Formula for Sum of an AP
Q1. Find the sum of the following APs:
(i) 2, 7, 12, ..., to 10 terms.
Here, a = 2
d = 7 - 2 = 5
n = 10
Since, Sn = n/2 [2a + (n - 1) d]
∴ S10 = [2 × 2 + (10 - 1) × 5]
⇒ S10 = 5 [4 + 9 × 5]
⇒ S10 = 5 [49] = 245
Thus, the sum of first 10 terms is 245.
(ii) - 37, - 33, - 29, ..., to 12 terms.
We have:
a = - 37
d = - 33 - (- 37) = 4
n = 12
∴ Sn = n/2 [2a + (n - 1) d]
⇒ S12 = 12/2 [2 (- 37) + (12 - 1) × 4]
= 6 [- 74 + 11 × 4]
= 6 [- 74 + 44]
= 6 × [- 30] = - 180
Thus, sum of first 12 terms = -180.
(iii) 0.6, 1.7, 2.8, ..., to 100 terms.
Here, a = 0.6
d = 1.7 - 0.6 = 1.1
n = 100
∴ Sn = n/2 [2a + (n - 1) d]
S100 = 100/2 [2 (0.6) + (100 - 1) × 1.1]
= 50 [1.2 + 99 × 1.1]
= 50 [1.2 + 108.9]
= 50 [110.1]
= 5505
Thus, the required sum of first 100 terms is 5505.
(iv) , ..., to 11 terms.
, ..., to 11 terms.
Here,
a = 1/15
d =
n = 11
∴ Sn = n/2 [2a + (n - 1) d]
S11 =
Thus, the required sum of first 11 terms = 33/20.
Q2. Find the sums given below:
(i) 
Here, a = 7
l = 84
Let n be the number of terms
∴ Tn = a + (n - 1) d
⇒
⇒
⇒ n = 22 + 1 = 23
Now,
⇒
Thus, the required sum =
(ii) 34 + 32 + 30 + ... + 10
Here, a = 34
d = 32 - 34 = - 2
l = 10
Let the number of terms be n
∴ Tn = 10
Now Tn = a + (n - 1) d
⇒ 10 = 34 + (n - 1) × (- 2)
⇒ (n - 1) × (- 2) = 10 - 34 = - 24
⇒
⇒ n = 13⇒
Now,
⇒
=
=
=
= 13 × 22 = 286
OR
S13 = n/2 (a + l)
Thus, the required sum is 286.
(iii) - 5 + (- 8) + (- 11) + ... + (- 230)
Here, a = - 5
d = - 8 - (- 5) = - 3
l = - 230
Let n be the number of terms.
∴ Tn = - 230
⇒ - 230 = - 5 + (n - 1) × (- 3)
⇒ (n - 1) × (- 3) = - 230 + 5 = - 225
⇒ n - 1 = -225/-3 = 75
⇒ n = 75 + 1 = 76
Now,
= 38 × (- 235)
= - 8930
∴ The required sum = - 8930.
Q3. In an AP:
(i) given a = 5, d = 3, an = 50, find n and Sn.
Here, a = 5, d = 3 and an = 50 = l
∵ an = a + (n - 1) d
∴ 50 = 5 + (n - 1) × 3
⇒ 50 - 5 = (n - 1) × 3
⇒ (n - 1) × 3 = 45
⇒ (n - 1) = 45/3 =15
⇒ n = 15 + 1 = 16
Now Sn = n/2 (a + l)
= 16/2 (5 + 50)
= 8 (55) = 440
Thus, n = 16 and Sn = 440
(ii) given a = 7, a13 = 35, find d and S13.
(ii) Here, a = 7 and a13 = 35 = l
∴ an = a + (n - 1) d
⇒ 35 = 7 + (13 - 1) d
⇒ 35 - 7 = 12d
⇒ 28 = 12d
⇒ d = 28/12 = 7/3
Now, using
Sn = n/2 (a + l)
S13 = 13/2 (7 + 35)
Sn = 273 and d = 7/3
(iii) given a12 = 37, d = 3, find a and S12.
Here, a12 = 37 = l and d = 3
Let the first term of the AP be ‘a’.
Now a12 = a + (12 - 1) d
⇒ 37 = a + 11d
⇒ 37 = a + 11 × 3
⇒ 37 = a + 33
⇒ a = 37 - 33 = 4
Now, Sn = n/2 (a + l)
⇒ S12 = 12/2 (4 + 37)
⇒ S12 = 6 × (41) = 246
Thus, a = 4 and S12 = 246
(iv) given a3 = 15, S10 = 125, find d and a10.
Here, a3 = 15 = l
S10 = 125
Let first term of the AP be ‘a’ and the common difference = d
∴ a3 = a + 2d
⇒ a + 2d = 15 ...(1)
Again Sn = n/2 [2a + (n - 1) d]
⇒ S10 = 10/2 [2a + (10 - 1) d]
⇒ 125 = 5 [2a + 9d]
⇒ 2a + 9d = 125/5 = 25
⇒ 2a + 9d = 25 ...(2)
Multiplying (1) by 2 and subtracting (2) from it, we get
2 [a + 2d = 15] - [2a + 9d = 25]
⇒ 2a + 4d - 2a - 9d = 30 - 25
⇒ - 5d = 5
⇒ d =5/-5 = -1
∴ From (1), a + 2 (- 1) = 15 ⇒ a = 15 + 2 ⇒ a = 17
Now, a10 = a + (10 - 1) d
= 17 + 9 × (- 1)
= 17 - 9 = 8
Thus, d = - 1 and a10 = 8
(v) given d = 5, S9 = 75, find a and a9.
Here, d = 5, S9 = 75
Let the first term of the AP is ‘a’.
∴ S9 = 9/2 [2a + (9 - 1) × 5]
⇒ 75 = 9/2 [2a + 40]
⇒
⇒ 50/3 = 2a + 40
⇒
⇒
Now, a9 = a + (9 - 1) d
=
=
Thus,
(vi) given a = 2, d = 8, Sn = 90, find n and an.
Here, a = 2, d = 8 and Sn = 90
∵ Sn = n/2 [2a + (n - 1) d]
∴ 90 = n/2 [2 × 2 + (n - 1) × 8]
⇒ 90 × 2 = 4n + n (n - 1) × 8
⇒ 180 = 4n + 8n2 - 8n
⇒ 180 = 8n2 - 4n
⇒ 45 = 2n2 - n
⇒ 2n2 - n - 45 = 0
⇒ 2n2 - 10n + 9n - 45 = 0
⇒ 2n (n - 5) + 9 (n - 5) = 0
⇒ (2n + 9) (n - 5) = 0
∴ Either
or n - 5 = 0 ⇒ n = 5
Butis not required. ∴n = 5
Now, an = a + (n - 1) d
⇒ a5 = 2 + (5 - 1) × 8
= 2 + 32 = 34
Thus, n = 5 and a5 = 34.
(vii) given a = 8, an = 62, Sn = 210, find n and d.
Here, a = 8, an = 62 = l and Sn = 210
Let the common difference = d
Now, Sn = 210
⇒ 210 = n/2 (a + l)
⇒ 210 = n/2 (8 + 62) =
∴ n = 210/35 = 6
Again an = a + (n - 1) d
⇒ 62 = 8 + (6 - 1) × d
⇒ 62 - 8 = 5d
⇒ 54 = 5d ⇒ d = 54/5
Thus, n = 6 and d = 54/5 .
(viii) given an = 4, d = 2, Sn = - 14, find n and a.
Here, an = 4, d = 2 and Sn = - 14
Let the first term be ‘a’.
∵ an = 4
∴ a + (n - 1) 2 = 4
⇒ a + 2n - 2 = 4
⇒ a = 4 - 2n + 2
⇒ a = 6 - 2n ...(1)
Also Sn = - 14
⇒ n/2 (a + l) = - 14
⇒ n/2 (a + 4) = - 14
⇒ n (a + 4) = - 28 ...(2)
Substituting the value of a from (1) into (2),
n [6 - 2n + 4] = - 28
⇒ n [10 - 2n] = - 28
⇒ 2n [5 - n] = - 28
⇒ n (5 - n) = - 14 [Dividing throughout by 2]
⇒ 5n - n2 + 14 = 0
⇒ n2 - 5n - 14 = 0
⇒ n2 - 7n + 2n - 14 = 0
⇒ n (n - 7) + 2 (n - 7) = 0
⇒ (n - 7) (n + 2) = 0
∴ Either n - 7 = 0 ⇒ n = 7
or n + 2 = 0 ⇒ n = - 2
But n cannot be negative,
∴ n = 7
Now, from (1), we have
a = 6 - 2 × 7 ⇒ a = - 8
Thus, a = - 8 and n = 7
(ix) given a = 3, n = 8, S = 192, find d.
Here, a = 3, n = 8 and Sn = 192
Let the common difference = d.
∵ Sn = n/2 [2a + (n - 1) d]
∴ 192 = 8/2 [2 (3) + (8 - 1) d]
⇒ 192 = 4 [6 + 7d]
⇒ 192 = 24 + 28d
⇒ 28d = 192 - 24 = 168
⇒ d = 168/28 =6
Thus, d = 6.
(x) given l = 28, S = 144, and there are total 9 terms. Find a.
(x) Here, l = 28 and S9 = 144
Let the first term be ‘a’.
Then Sn = n/2 (a + l)
⇒ S9 = 9/2 (a + 28)
⇒ 144 = 9/2 (a + 28)
⇒
⇒ a = 32 - 28 = 4
Thus, a = 4.
Q4. How many terms of the AP: 9, 17, 25, ... must be taken to give a sum of 636?
Here, a = 9
d = 17 - 9 = 8
Sn = 636
∵ Sn = n/2 [2a + (n - 1) d] = 636
∴ n/2 [(2 × 9) + (n - 1) × 8] = 636
⇒ n [18 + (n - 1) × 8] = 1272
⇒ n (8n + 10) = 1272
⇒ 8n2 + 10n - 1272 = 0
⇒ 4n2 + 5n - 636 = 0
⇒ 4n2 + 53n - 48n - 636 = 0
⇒ n (4n + 53) - 12 (4n + 53) = 0
⇒ (n - 12) (4n + 53) = 0
⇒ n = 12 and
Rejecting, we have n = 12.
Q5. The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
Here, a = 5
l = 45 = Tn
Sn = 400
∵ Tn = a + (n - 1) d
∴ 45 = 5 + (n - 1) d
⇒ (n - 1) d = 45 – 5
⇒ (n - 1) d = 40 ...(1)
Also Sn = n/2 (a + l)
⇒ 400 = n/2 (5 + 45)
⇒ 400 × 2 = n × 50
⇒
From (1), we get
(16 - 1) d = 40
⇒ 15d = 40
⇒ d = 40/15 = 8/3
|
5 videos|378 docs|164 tests
|

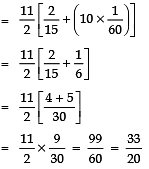
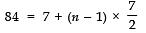
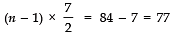
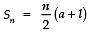
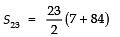
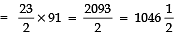
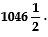
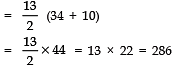
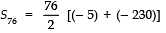
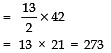
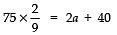
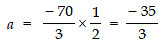
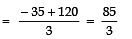
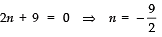
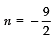 is not required. ∴n = 5
is not required. ∴n = 5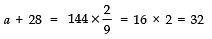
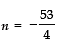
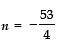 , we have n = 12.
, we have n = 12.