Best Study Material for Year 11 Exam
Year 11 Exam > Year 11 Notes > Mathematics for GCSE/IGCSE > Exact Trig Values
Exact Trig Values | Mathematics for GCSE/IGCSE - Year 11 PDF Download
What are exact values in trigonometry?
- Exact values in trigonometry refer to specific values of sine, cosine, and tangent for certain angles that can be expressed precisely using fractions and surds.
- You should be able to recognize and derive these values geometrically.
- It is essential to know the exact values for angles of 0°, 30°, 45°, 60°, 90°, 180°, and their multiples.
- The exact values you are expected to know are summarised here:
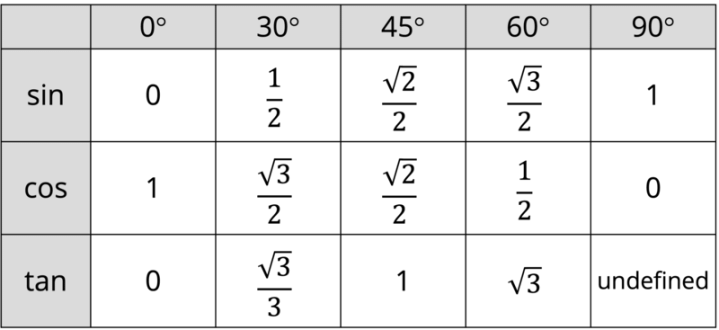
- Note that the values of sin θ going from 0° to 90° match those of cos θ going from 90° to 0°
How are exact values in trigonometry derived?
There are two special right-angled triangles that provide exact values for trigonometric functions.
- Consider a right-angled triangle with a hypotenuse of 2 units and a shorter side length of 1 unit. Applying Pythagoras’ theorem, the third side will be √3 units. The angles are 90°, 60°, and 30°. Utilizing SOHCAHTOA:
- Sin 60° = √3/2, Sin 30° = 1/2
- Cos 60° = 1/2, Cos 30° = √3/2
- Tan 60° = √3, Tan 30° = (√3)/3
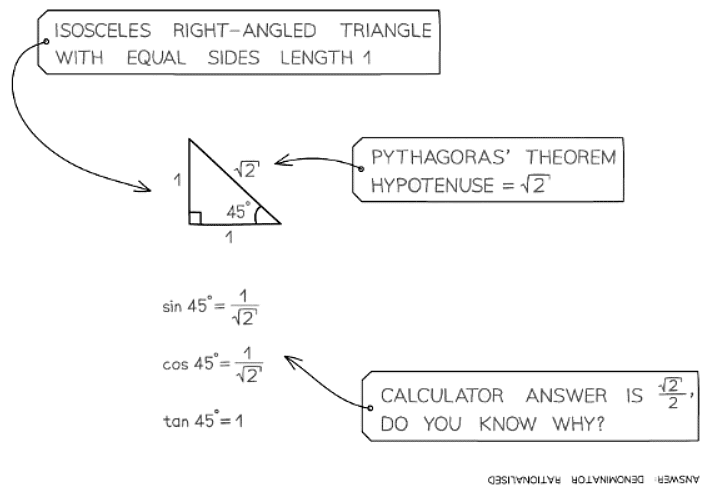
- Now, consider an isosceles triangle with two equal side lengths (the opposite and adjacent) of 1 unit. Applying Pythagoras’ theorem, its hypotenuse will be √2 units. The two equal angles are 45°. Applying SOHCAHTOA:
- Sin 45° = 1/√2 = √2/2
- Cos 45° = 1/√2 = √2/2
- Tan 45° = 1
The document Exact Trig Values | Mathematics for GCSE/IGCSE - Year 11 is a part of the Year 11 Course Mathematics for GCSE/IGCSE.
All you need of Year 11 at this link: Year 11
|
84 videos|120 docs
|
FAQs on Exact Trig Values - Mathematics for GCSE/IGCSE - Year 11
| 1. What are exact values in trigonometry? |  |
| 2. How are exact values in trigonometry derived? | |
Ans. Exact values in trigonometry are derived using special right triangles, unit circle definitions, and trigonometric identities to find the exact values of sine, cosine, and tangent of common angles such as 30°, 45°, and 60°.
| 3. Why are exact values important in trigonometry? | |
Ans. Exact values in trigonometry are important because they allow for precise calculations and simplification of trigonometric expressions without rounding errors that can occur when using approximate values from a calculator.
| 4. What are some common exact trigonometric values used in trigonometry? | |
Ans. Some common exact trigonometric values used in trigonometry include sin(30°) = 1/2, cos(45°) = √2/2, tan(60°) = √3, and their respective reciprocal values.
| 5. How can exact trigonometric values be applied in real-world scenarios? | |
Ans. Exact trigonometric values can be applied in real-world scenarios such as engineering, physics, and geometry to calculate angles, distances, heights, and other measurements accurately without the need for approximation.
Related Exams
About this Document
Apr 11, 2025
Last updated
Document Description: Exact Trig Values for Year 11 2025 is part of Mathematics for GCSE/IGCSE preparation.
The notes and questions for Exact Trig Values have been prepared according to the Year 11 exam syllabus. Information about Exact Trig Values covers topics
like What are exact values in trigonometry?, How are exact values in trigonometry derived? and Exact Trig Values Example, for Year 11 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Exact Trig Values.
Introduction of Exact Trig Values in English is available as part of our Mathematics for GCSE/IGCSE
for Year 11 & Exact Trig Values in Hindi for Mathematics for GCSE/IGCSE course.
Download more important topics related with notes, lectures and mock test series for Year 11
Exam by signing up for free. Year 11: Exact Trig Values | Mathematics for GCSE/IGCSE - Year 11
Description
Full syllabus notes, lecture & questions for Exact Trig Values | Mathematics for GCSE/IGCSE - Year 11 - Year 11 | Plus excerises question with solution to help you revise complete syllabus for Mathematics for GCSE/IGCSE | Best notes, free PDF download
Information about Exact Trig Values
In this doc you can find the meaning of Exact Trig Values defined & explained in the simplest way possible. Besides explaining types of
Exact Trig Values theory, EduRev gives you an ample number of questions to practice Exact Trig Values tests, examples and also practice Year 11
tests
Related Searches
Viva Questions
,Exact Trig Values | Mathematics for GCSE/IGCSE - Year 11
,Semester Notes
,Objective type Questions
,MCQs
,mock tests for examination
,Important questions
,video lectures
,Exam
,ppt
,Free
,past year papers
,Previous Year Questions with Solutions
,Extra Questions
,study material
,Exact Trig Values | Mathematics for GCSE/IGCSE - Year 11
,practice quizzes
,Sample Paper
,Exact Trig Values | Mathematics for GCSE/IGCSE - Year 11
,Summary
,shortcuts and tricks
;
Additional Information about Exact Trig Values for Year 11 Preparation
Exact Trig Values Free PDF Download
The Exact Trig Values is an invaluable resource that delves deep into the core of the Year 11 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Exact Trig Values now and kickstart your journey towards success in the Year 11 exam.
Importance of Exact Trig Values
The importance of Exact Trig Values cannot be overstated, especially for Year 11 aspirants.
This document holds the key to success in the Year 11 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Exact Trig Values Notes
Exact Trig Values Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Exact Trig Values.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Exact Trig Values Notes on EduRev are your ultimate resource for success.
Exact Trig Values Year 11 Questions
The "Exact Trig Values Year 11 Questions" guide is a valuable resource for all aspiring students preparing for the
Year 11 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Exact Trig Values on the App
Students of Year 11 can study Exact Trig Values alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Exact Trig Values,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Exact Trig Values is prepared as per the latest Year 11 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup