Expected Value | Additional Topics for IIT JAM Mathematics PDF Download
Expected Values of Random Variables
We already looked at finding the mean in the section on averages. Random variables also have means but their means are not calculated by simply adding up the different variables.
The mean of a random variable is more commonly referred to as its Expected Value, i.e. the value you expect to obtain should you carry out some experiment whose outcomes are represented by the random variable.
The expected value of a random variable X is denoted by
E(X)
Given that the random variable X is discrete and has a probability distribution f(x), the expected value of the random variable is given by: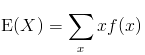
Given that the random variable X is continuous and has a probability distribution f(x), the expected value of the random variable is given by: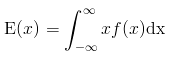
Example 1:
The probability distribution of X, the number of red cars John meets on his way to work each morning, is given by the following table:
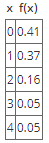
Find the number of red cars that John expects to run into each morning on his way to work.
Solution:
This question is asking us to find the average number of red cars that John runs into on his way to work. What makes this different from an ordinary mean question is that the odds (probability) of running into a given number of cars are not the same.
Since X is a discrete random variable, the expected value is given by:
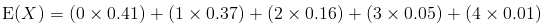
E(X) = 0.88
Although you wouldn't expect to run into 0.88 cars, let's pretend that the above is multiplied by 100 to get the actual number of cars that John comes across on his way to work.
Example 2:
A certain software company uses a certain software to check for errors on any of the programs it builds and then discards the software if the errors found exceed a certain number. Given that the number of errors found is represented by a random variable X whose density function is given by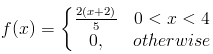
Find the average number of errors the company expects to find in a given program.
Solution:
The random variable X is given as a continuous random variable, thus its expected value can be found as follows:
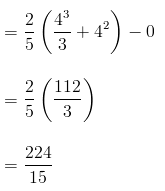
The company should expect to find approximately 14.93 errors.
Expected Value of an Arbitrary Function
In some cases, an event is represented by a function of the random variable which we refer to as g(X). To find the expected value of this event, we find substitute the function for the variable in the expectation formula, i.e.
For a discrete variable X: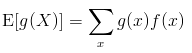
For a continuous random variable X:
Example 3:
X is a random variable given by the following probability distribution:
Given that g(X) = (x2 + 2), find E[g(X)]
Solution:
For a discrete random variable X, the expected value of an arbitrary function is given by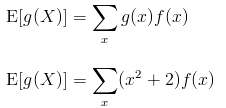
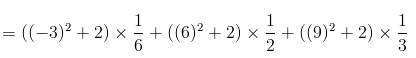
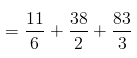
= 48.5
Example 4:
Given that X is a continuous random variable whose PDF is given by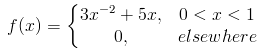
find E[g(X)] given that g(X) = 3x2
Solution:
For a continuous random variable, the expected value of an arbitrary function of the random variable g(X) is given by
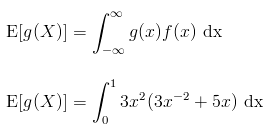
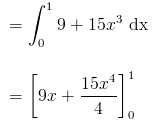
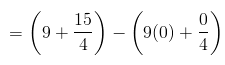
= 51/4
= 12.75
Expected Value of Joint Random Variables
For a pair of random variables X and Y with a joint probability distribution f(x,y), the expected value can be found by use of an arbitrary function of the random variables g(X,Y) such that
- for a discrete pair of random variables X and Y
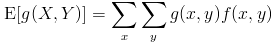
- for a continuous set of random variables X and Y
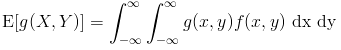
Example 5:
Given a pair of discrete random variables X and Y whose joint probability distribution function is given by the table below;
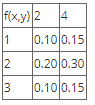
Find the expected value of the function g(X,Y) given that
g(X, Y) = 2X + Y
Solution:
For a pair of discrete random variables, the joint probability distribution is given by: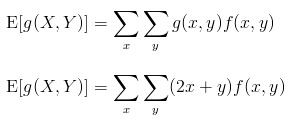
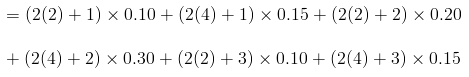
= 9.6
Example 6:
Given the random variables X and Y and the function g(X,Y) = XY, find E[G(X,Y)] if the joint density function is given by;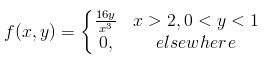
Solution:
The expected value is given by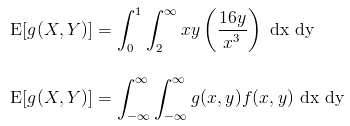
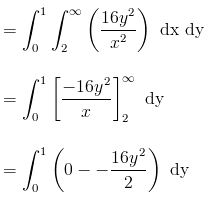
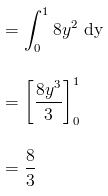
|
2 videos|45 docs|4 tests
|
FAQs on Expected Value - Additional Topics for IIT JAM Mathematics
| 1. What is expected value in mathematics? |  |
| 2. How is expected value calculated? |  |
| 3. What is the significance of expected value in decision-making? |  |
| 4. Can expected value be negative? |  |
| 5. How is expected value applied in real-life scenarios? |  |
















