Expression Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Expression tree in data structure
The expression tree is a tree used to represent the various expressions. The tree data structure is used to represent the expressional statements. In this tree, the internal node always denotes the operators.
- The leaf nodes always denote the operands.
- The operations are always performed on these operands.
- The operator present in the depth of the tree is always at the highest priority.
- The operator, which is not much at the depth in the tree, is always at the lowest priority compared to the operators lying at the depth.
- The operand will always present at a depth of the tree; hence it is considered the highest priority among all the operators.
- In short, we can summarize it as the value present at a depth of the tree is at the highest priority compared with the other operators present at the top of the tree.
- The main use of these expression trees is that it is used to evaluate, analyze and modify the various expressions.
- It is also used to find out the associativity of each operator in the expression.
- For example, the + operator is the left-associative and / is the right-associative.
- The dilemma of this associativity has been cleared by using the expression trees.
- These expression trees are formed by using a context-free grammar.
- We have associated a rule in context-free grammars in front of each grammar production.
- These rules are also known as semantic rules, and by using these semantic rules, we can be easily able to construct the expression trees.
- It is one of the major parts of compiler design and belongs to the semantic analysis phase.
- In this semantic analysis, we will use the syntax-directed translations, and in the form of output, we will produce the annotated parse tree.
- An annotated parse tree is nothing but the simple parse associated with the type attribute and each production rule.
- The main objective of using the expression trees is to make complex expressions and can be easily be evaluated using these expression trees.
- It is immutable, and once we have created an expression tree, we can not change it or modify it further.
- To make more modifications, it is required to construct the new expression tree wholly.
- It is also used to solve the postfix, prefix, and infix expression evaluation.
Expression trees play a very important role in representing the language-level code in the form of the data, which is mainly stored in the tree-like structure. It is also used in the memory representation of the lambda expression. Using the tree data structure, we can express the lambda expression more transparently and explicitly. It is first created to convert the code segment onto the data segment so that the expression can easily be evaluated.
The expression tree is a binary tree in which each external or leaf node corresponds to the operand and each internal or parent node corresponds to the operators so for example expression tree for 7 + ((1+8)*3) would be:
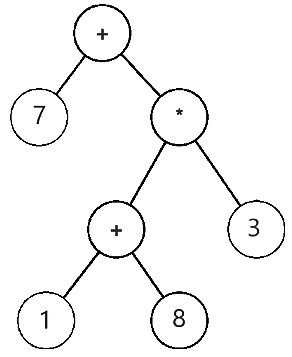
Let S be the expression tree
If S is not null, then
If S.value is an operand, then
Return S.value
x = solve(S.left)
y = solve(S.right)
Return calculate(x, y, S.value)
Here in the above example, the expression tree used context-free grammar.
We have some productions associated with some production rules in this grammar, mainly known as semantic rules. We can define the result-producing from the corresponding production rules using these semantic rules. Here we have used the value parameter, which will calculate the result and return it to the grammar's start symbol. S.left will calculate the left child of the node, and similarly, the right child of the node can be calculated using the S.right parameter.
Use of Expression tree
- The main objective of using the expression trees is to make complex expressions and can be easily be evaluated using these expression trees.
- It is also used to find out the associativity of each operator in the expression.
- It is also used to solve the postfix, prefix, and infix expression evaluation.
Implementation of an Expression tree
To implement the expression tree and write its program, we will be required to use a stack data structure.
As we know that the stack is based on the last in first out LIFO principle, the data element pushed recently into the stack has been popped out whenever required. For its implementation, the main two operations of the stack, push and pop, are used. Using the push operation, we will push the data element into the stack, and by using the pop operation, we will remove the data element from the stack.
Main functions of the stack in the expression tree implementation
First of all, we will do scanning of the given expression into left to the right manner, then one by one check the identified character,
- If a scanned character is an operand, we will apply the push operation and push it into the stack.
- If a scanned character is an operator, we will apply the pop operation into it to remove the two values from the stack to make them its child, and after then we will push back the current parent node into the stack.
Implementation of Expression tree in C Programming language
// C program for expression tree implementation
#include <stdio.h>
#include <stdlib.h>
/* The below structure node is defined as a node of a binary tree consists
of left child and the right child, along with the pointer next which points to the next node */
struct node
{
char info ;
struct node* l ;
struct node* r ;
struct node* nxt ;
};
struct node *head=NULL;
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newnode(char data)
{
struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ;
node->info = data ;
node->l = NULL ;
node->r = NULL ;
node->nxt = NULL ;
return ( node ) ;
}
void Inorder(struct node* node)
{
if ( node == NULL)
return ;
else
{
/* first recur on left child */
Inorder ( node->l ) ;
/* then print the data of node */
printf ( "%c " , node->info ) ;
/* now recur on right child */
Inorder ( node->r ) ;
}
}
void push ( struct node* x )
{
if ( head == NULL )
head = x ;
else
{
( x )->nxt = head ;
head = x ;
}
// struct node* temp ;
// while ( temp != NULL )
// {
// printf ( " %c " , temp->info ) ;
// temp = temp->nxt ;
// }
}
struct node* pop()
{
// Poping out the top most [pointed with head] element
struct node* n = head ;
head = head->nxt ;
return n ;
}
int main()
{
char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ;
int n = sizeof(t) / sizeof(t[0]) ;
int i ;
struct node *p , *q , *s ;
for ( i = 0 ; i < n ; i++ )
{
// if read character is operator then popping two
// other elements from stack and making a binary
// tree
if ( t[i] == '+' || t[i] == '-' || t[i] == '*' || t[i] == '/' || t[i] == '^' )
{
s = newnode ( t [ i ] ) ;
p = pop() ;
q = pop() ;
s->l = q ;
s->r = p;
push(s);
}
else {
s = newnode ( t [ i ] ) ;
push ( s ) ;
}
}
printf ( " The Inorder Traversal of Expression Tree: " ) ;
Inorder ( s ) ;
return 0 ;
}
The output of the above program is:
X + Y * Z / W
Implementation of Expression tree in C++ Programming language
// C++ program for expression tree
#include <bits/stdc++.h>
using namespace std ;
/* The below class node is defined as a node of a binary tree consists
of left child and the right child, along with the pointer next which points to the next node */
class node
{
public:
char info ;
node* l ;
node* r ;
node* nxt = NULL ;
node ( char c )
{
this->info = c ;
l = NULL ;
r = NULL ;
}
node()
{
l = NULL ;
r = NULL ;
}
friend class Stack ;
friend class tree ;
} ;
class Stack
{
node* head = NULL ;
public:
void push ( node* ) ;
node* pop() ;
friend class tree ;
} ;
class tree
{
public:
void inorder ( node* x )
{
// cout<<"Tree in InOrder Traversal is: "<<endl;
if ( x == NULL )
return ;
else
{
inorder ( x->l ) ;
cout << x->info << " " ;
inorder ( x->r ) ;
}
}
} ;
void Stack::push( node* x )
{
if ( head == NULL )
{
head = x ;
}
// We are inserting here nodes at the top of the stack [following LIFO principle]
else
{
x->nxt = head ;
head = x ;
}
}
node* Stack::pop()
{
// Poping out the top most [ pointed with head ] element
node* p = head ;
head = head->nxt ;
return p ;
}
int main()
{
string str = "XYZ*+W/" ;
// If you wish take input from user:
//cout << "Insert Postorder Expression: " << endl;
//cin >> s;
Stack s ;
tree t ;
node *p, *q, *re;
int n = str.length() ;
for ( int i = 0 ; i < n ; i++ )
{
if ( str[ i ] == '+' || str[ i ] == '-' || str[ i ] == '*' || str[ i ] == '/' || str[ i ] == '^')
{
re = new node( str[i] ) ;
p = s.pop() ;
q = s.pop() ;
re->l = q ;
re->r = p ;
s.push(re) ;
}
else
{
re = new node( str[ i ] ) ;
s.push(re) ;
}
}
cout << " The Inorder Traversal of Expression Tree: " ;
t.inorder(re) ;
return 0 ;
}
The output of the above program is:
X + Y * Z / W
Implementation of Expression tree in Java Programming language
// Java program for expression tree
import java.util.* ;
/* The below class node is defined as a node of a binary tree consists
of left child and the right child, along with the pointer next which points to the next node */
class Node
{
char info ;
Node l , r ;
public Node(char data)
{
this.info = data ;
l = null ;
r = null ;
}
}
public class Main
{
public static boolean isOperator ( char ch )
{
if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' )
{
return true ;
}
return false ;
}
public static Node Tree ( String postfix )
{
Stack<Node> st = new Stack<Node>();
Node t1,t2,temp ;
for ( int i = 0 ; i < postfix.length(); i++ )
{
if ( !isOperator( postfix.charAt(i) ) )
{
temp = new Node( postfix.charAt(i) ) ;
st.push( temp ) ;
}
else
{
temp = new Node ( postfix.charAt(i) ) ;
t1 = st.pop() ;
t2 = st.pop() ;
temp.l = t2 ;
temp.r = t1 ;
st.push(temp) ;
}
}
temp = st.pop() ;
return temp ;
}
public static void inorder( Node parent ){
if ( parent == null ) return ;
inorder ( parent.l ) ;
System.out.print ( parent.info ) ;
inorder ( parent.r ) ;
}
public static void main( String[] args )
{
String postfix = "XYZ*+W/" ;
Node r = Tree( postfix ) ;
inorder ( r ) ;
}
}
The output of the above program is:
X + Y * Z / W
|
159 docs|30 tests
|
















