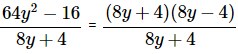Factoring Solved Examples | The Complete SAT Course - Class 10 PDF Download
Example 1: Algebra
If 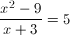 , and
, and 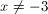 , what is the value of
, what is the value of  ?
?
(a) 0
(b) -6
(c) 6
(d) 8
(e) –8
Correct Answer is Option (d)
The numerator on the left can be factored so the expression becomeswhich can be simplified to (x - 3) = 5.
Then you can solve for x by adding 3 to both sides of the equation, so x = 8
Example 2: Factoring
Factor the following variable (x2 + 18x + 72)
(a) (x + 6) (x – 12)
(b) (x – 6) (x – 12)
(c) (x + 18) (x + 72)
(d) (x + 6) (x + 12)
(e) (x – 6) (x + 12)
Correct Answer is Option (d)
You need to find two numbers that multiply to give 72 and add up to give 18
easiest way: write the multiples of 72:
1, 72
2, 36
3, 24
4, 18
6, 12: these add up to 18
(x + 6)(x + 12)
Example 3: How To Factor A Variable
Factor 9x2 + 12x + 4.
(a) (9x + 4)(9x + 4)
(b) (9x + 4)(9x – 4)
(c) (3x – 2)(3x – 2)
(d) (3x + 2)(3x – 2)
(e) (3x + 2)(3x + 2)
Correct Answer is Option (e)
Nothing common cancels at the beginning. To factor this, we need to find two numbers that multiply to 9 x 4 = 36 and sum to 12. 6 and 6 work.
So 9x2 + 12x + 4 = 9x2 + 6x + 6x + 4
Let's look at the first two terms and last two terms separately to begin with. 9x2 + 6x can be simplified to 3x(3x + 2) and 6x + 4 can be simplified into 2(3x + 2). Putting these together gets us
9x2 + 12x + 4
= 9x2 + 6x + 6x + 4
= 3x(3x + 2) + 2(3x + 2)
= (3x + 2)(3x + 2)
This is as far as we can factor.
Example 4 : Factoring
Factor: −12x2 + 27
(a) −3(2x + 3)(2x + 3)
(b) −3(2x + 3)(2x − 3)
(c) −3(4x2 − 9)
(d) (2x + 3)(2x + 3)
(e) (2x + 3)(2x − 3)
Correct Answer is Option (b)
We can first factor out −3:
−3(4x2 - 9)
This factors further because there is a difference of squares:
−3(2x + 3)(2x − 3)
Example 5: How To Factor A Variable
Factor to the simplest form: x3 + 2x2 + a + bx2 + 2
(a) 3x3 + a + b + 2
(b) x3 + (2 + b)(x2) + a + 2
(c) x2(x + 2 + b + a + 2)
(d) x2(x + 2 + b) + a + 2
(e) x(x2 + 2x + bx) + a + 2
Correct Answer is Option (d)
Group all the terms with the x variable.
x3 + 2x2 + a + bx2 + 2 = (x3 + 2x2 + bx2) + a + 2
Pull out an x2 term from parentheses.
(x3 + 2x2 + bx2) + a + 2 = x2(x + 2 + b) + a + 2
There are no more common factors.
The correct answer is: x2(x + 2 + b) + a + 2
Example 6: Algebra
Factor and simplify: 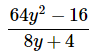
(a) 8y − 12
(b) −4
(c) 8y
(d) 8y − 4
(e) 8y + 4
Correct Answer is Option (d)
64y2 − 16 is a difference of squares.
The difference of squares formula is a2 − b2 = (a − b)(a + b).
Therefore,
= 8y − 4
|
433 videos|220 docs|166 tests
|