JEE Advanced (Fill in the Blanks): Trigonometric Functions & Equations | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Suppose sin3x.sin 3x =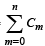 cos mx is an identity in x, where C0, C1, ___Cn are constants, and Cn ≠ 0. Then the value of n is _________. (1981 - 2 Marks)
cos mx is an identity in x, where C0, C1, ___Cn are constants, and Cn ≠ 0. Then the value of n is _________. (1981 - 2 Marks)
Ans. 6
Sol. sin3x . sin 3x =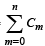 cos mx
cos mx
sin3x.sin 3x =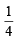 [3 sinx – sin3x] sin 3x
[3 sinx – sin3x] sin 3x
=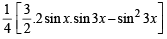
=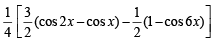
= 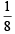 [ cos 6x + 3 cos 2x - 3 cosx - 1]
[ cos 6x + 3 cos 2x - 3 cosx - 1]
We observe that on LHS 6 is the max value of m.
∴n = 6
Q.2. The solution set of the system of equations x + y =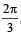 , cosx + cosy =
, cosx + cosy =  where x and y are real, is _________. (1987 - 2 Marks)
where x and y are real, is _________. (1987 - 2 Marks)
Ans. φ
Sol. The equations are x + y = 2π /3 ... (i)
cos x + cos y = 3/2 ...(ii)
From eq.
(ii) 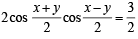
⇒ 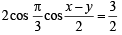 [Using eq. (i)]
[Using eq. (i)]
⇒ 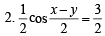
⇒ 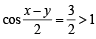
Which has no solution.
∴ The solution of given equations is φ.
Q.3. The set of all x in the interval [0,π] for which 2sin2 x – 3 sin x + 1 ≥ 0, is _________. (1987 - 2 Marks)
Ans.
Sol. We have 2 sin2 x – 3 sin x + 1 ≥ 0
⇒ (2 sin x – 1) (sin x – 1) ≥ 0
⇒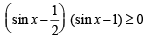
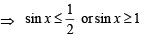
But we know that sin x ≤ 1 and sin x ≥ 0 for x ∈ [0, π]
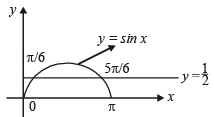
⇒ either sin x = 1 or 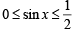
⇒ either x = π/2 or 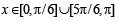
Combining, we get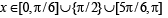
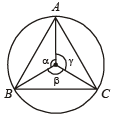
Q.4. The sides of a triangle inscribed in a given circle subtend angles α, β and γ at the centre. The minimum value of the arithmetic mean of 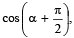
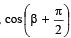 and
and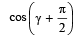 is equal to _________. (1987 - 2 Marks)
is equal to _________. (1987 - 2 Marks)
Ans. 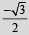
Sol. We know that A.M. ≥ G.M.
⇒ Min value of AM. is obtained when AM = GM
⇒ The quantities whose AM is being taken are equal.
i.e., Cos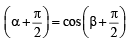
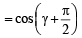
⇒ sin α = sin β = sinγ
Also α +β + γ= 360° ⇒ α = β = γ=120° = 2π/3
∴ Min value of A.M.
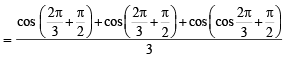
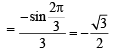
Q.5. The value of 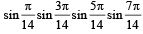
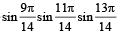 is equal to _________. (1991 - 2 Marks)
is equal to _________. (1991 - 2 Marks)
Ans. 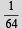
Sol.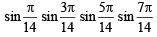
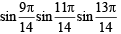
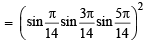
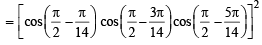
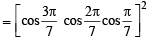
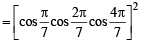
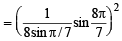
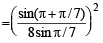
=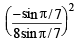
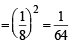
Q.6. If K = sin(π/18) sin(5π/18) sin(7π/18), then the numerical value of K is _________ . (1993 - 2 Marks)
Ans. 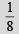
Sol. 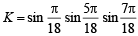
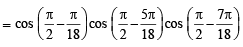
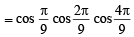
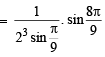
[Using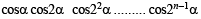
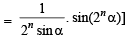
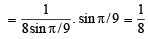
Q.7. If A > 0,B>0 and A + B = π/3, then the maximum value of tan A tan B is_________ . (1993 - 2 Marks)
Ans. 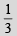
Sol. A + B = π/3 ⇒ tan (A +B ) = 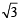
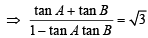
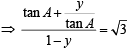
[where y = tan A tan B]
⇒ tan2 A + 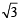 (y – 1) tan A + y = 0
(y – 1) tan A + y = 0
For real value of tan A, 3(y – 1)2 – 4y ≥ 0
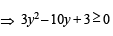
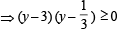
⇒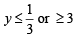
But A, B > 0 and A + B = π/3
⇒ A, B < π/3
⇒ tan A tan B < 3
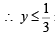 i.e., max. value of y is 1/3.
i.e., max. value of y is 1/3.
Q.8. General value of θ satisfying the equation tan2θ + sec 2θ = 1 is_________ . (1996 - 1 Mark)
Ans.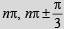
Sol. tan2θ + sec 2θ= 1 where t = tanθ
where t = tanθ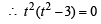
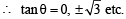
which means θ = nπ and θ =nπ±π/3
Q.9. The real roots of the equation cos7 x + sin4 x=1 in the interval (–π, π) are ______, ______, and _________ . (1997 - 2 Marks)
Ans.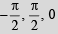
Sol. cos7 x = 1– sin4 x = (1– sin2 x) (1 + sin2 x) = cos2 x (1 + sin2 x)
∴ cos x = 0
or x = π/2, – π/2
or cos5 x = 1 + sin2 x or cos5 x – sin2 x = 1
Now maximum value of each cos x or sin x is 1.
Hence the above equation will hold when cos x = 1 and sin x = 0. Both these imply x = 0
Hence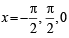
|
446 docs|929 tests
|





















