Fill in the Blanks: Quadratic Equation and Inequations (Inequalities) | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download

Q.1. The coefficient of x⁹⁹ in the polynomial (x – 1) (x – 2) ....(x – 100) is ................... (1982 - 2 Marks)

Ans. Sol. Given polynomial :

(x – 1) (x – 2) (x – 3) . . . (x – 100)

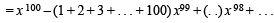
Here coeff. of x ⁹⁹ = – (1 + 2 + 3 + ... + 100)

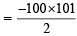 = -5050

Q.2. If 2 + i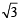 is a root of the equation x² + px +q= 0 , where p and q are real, then (p, q) = ( ................... , ................... ). (1982 - 2 Marks)

Ans. Sol. As p and q are real;and one root is 2 + i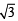, other should be 2 – i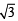
Then p = – (sum of roots) = – 4,
q = product of roots = 4 + 3 = 7.

Q.3. If the product of the roots of the equation  x² – 3kx + 2 e^2lnk – 1 = 0 is 7, then the roots are real fork = ................... (1984 - 2 Marks)

Ans. Sol. The given equation is x² - 3kx + 2e^2lnk - 1=0

Or x ² - 3kx + (2k² - 1)=0

Here product of roots = 2k² –1

∴ 2k ² - 1 = 7 ⇒ k²=4 ⇒ k= 2, –2

Now for real roots we must have D ≥ 0

⇒ 9k ² – 4(2k ² - 1) ≥ 0 ⇒k² + 4≥0

Which is true for all k. Thus k = 2, – 2

But for k = –2,  ln k is not define

∴  Rejecting k = –2, we get k = 2

Q.4. If the quadratic equations x² + ax + b = 0 and x² + bx + a = 0 (a ¹b) have a common root, then the numerical value of a + b is ................... (1986 - 2 Marks)

Ans. Sol. ∵  x = 1 reduces both the equations to 1 + a + b = 0

∴  1 is the common root. for a + b = –1

∴  Numerical value of a + b = 1

Q.5. The solution of equation log7 log5 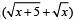  = 0 is ................... (1986 - 2 Marks)

Ans. Sol. 

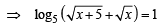 NOTE THIS STEP

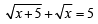⇒  ⇒ x+5 = 25+ x-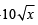

⇒ 2 = 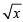⇒ x=4 which satisfies the given equation.

Q.6. If x < 0, y < 0, x + y + 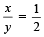  and (x + y)  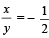,  then x = ........ and y = ...... (1990 -  2 Marks)

Ans. Sol. Given     x < 0,   y < 0

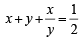and 

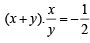
Let    x + y = a    and 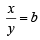  .... (1)

∴ We get a + b = 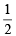and  ab = –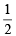

Solving these two, we get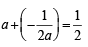

⇒ 2a² -a - 1=0 ⇒ a = 1,  – 1/2  ⇒ b = – 1/2,  1

∴  (1) ⇒ x + y = 1  and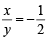   

or x + y = 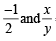= 1 But   x,  y < 0

∴ x + y < 0 ⇒ x + y = 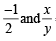= 1

On solving, we get  x = – 1/4 and y = –1/4.

Q.7. Let n and k be positive such that 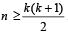. The number of solutions 

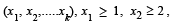
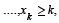   all integers, satisfying x₁ + x₂ + ....+ x_k = n, is ................... (1996 - 2 Marks)

Ans. Sol. We have x₁ + x₂ + ...............+ x_k = n  .... (1)

where 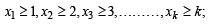   all integers

Let  y₁ = x₁ - 1, y₂= x₂ - 2.................. y_k = x_k - k

so that y₁, y₂ ,.........,y_k ≥0

Substituting the values of x₁, x₂ , ............,x_k in equation .. (1)

We get y₁ + y₂ +........ y_k = n - (1 + 2 + 3K+k)

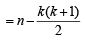 .... (2)

Now keeping in mind that number of solutions of the equation

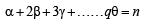
for α, β, γ , .........θ∈ I and each is ≥ 0, is given by coeff of xⁿ in

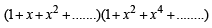
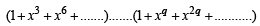
We find that no. of solutions of equation (2)

                                                 NOTE THIS STEP

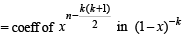
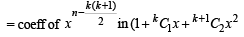
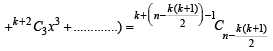
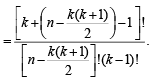
Q. 8. The sum of all the real roots of the equation  | x – 2 |² + | x – 2 | – 2 = 0 is ................... (1997 - 2 Marks)

Ans. Sol. |x– 2|²+ |x-2|-2=0

Case 1. x ≥ 2

⇒ (x - 2)² + (x - 2) - 2= 0

⇒ x² - 3x = 0 ⇒ x(x - 3)=0

⇒ x = 0, 3 (0 is rejected as x ≥ 2)

⇒ x  = 3                ....(1)

Case 2. x < 2

{-( x - 2)} - (x- 2)- 2 = 0

⇒ x² + 4 - 4x -x=0 ⇒ (x -1)(x - 4)= 0

⇒ x = 1,  4 (4 is rejected as x < 2)

⇒ x = 1                ....(2)

Therefore, the sum of the roots is 3 + 1= 4.