Fill in the Blanks: Vector Algebra and Three Dimensional Geometry | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q. 1. Let 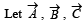 be vectors of length 3, 4, 5 respectively. Let
be vectors of length 3, 4, 5 respectively. Let 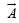 be perpendicular to
be perpendicular to 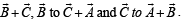 Then the length of vector
Then the length of vector 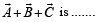 (1981 - 2 Marks)
(1981 - 2 Marks)
Ans. 5√2
Solution.
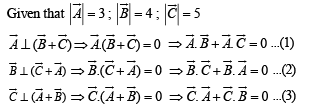
Adding (1), (2) and (3) we get
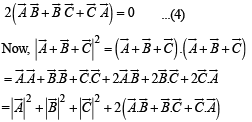
= 50 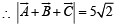
Q. 2. The unit vector perpendicular to the plane determined by P(1, –1, 2), Q (2, 0, –1) and R(0, 2, 1) is ....... (1983 - 1 Mark)
Ans. 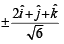
Solution. Required unit vector, 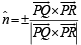
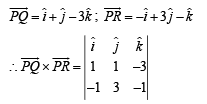
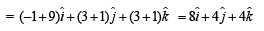
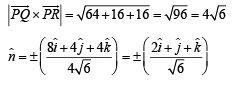
Q. 3. The area of the triangle whose vertices are A (1, –1, 2), B (2, 1, –1), C( 3, – 1, 2) is ....... (1983 - 1 Mark)
Ans. 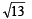
Solution.
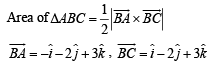

Q. 4. A, B, C and D, are four points in a plane with position vectors a, b, c and d respectively such that
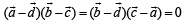
The point D, then, is the ................... of the triangle ABC. (1984 - 2 Marks)
Ans. orthocen tre
Solution. Given that  are position vectors of points A, B, C and D respectively, such tha
are position vectors of points A, B, C and D respectively, such tha
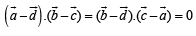
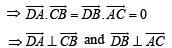
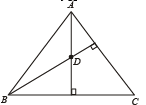
Clearly D is orthocentre of DΔABC
Q. 5. 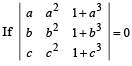 and the vectors
and the vectors 
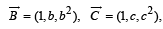 are non -coplanar, then the product abc = ....... (1985 - 2 Marks)
are non -coplanar, then the product abc = ....... (1985 - 2 Marks)
Ans. –1
Solution. 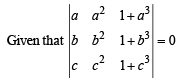
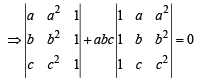
Operating  in first determinant
in first determinant

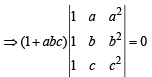
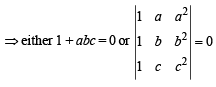
Also given that the vectors  are noncoplanar
are noncoplanar
i.e., 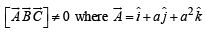
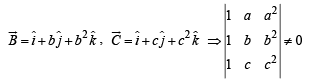
∴ We must have 1 + abc = 0 ⇒ abc = – 1
Q. 6. If 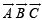 are three non-coplanar vectors, then –
are three non-coplanar vectors, then –
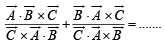 (1985 - 2 Marks)
(1985 - 2 Marks)
Ans. 0
Solution. As given that 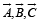 are three noncoplan ar vectors, therefore,
are three noncoplan ar vectors, therefore, 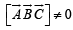
Also by the property of scalar triple product we have
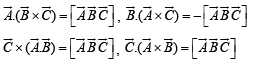
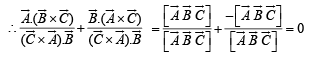
Q. 7. 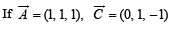 are given vectors, then a vector B satisfying the equations
are given vectors, then a vector B satisfying the equations 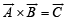 and
and 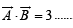 (1985 - 2 Marks)
(1985 - 2 Marks)
Ans. 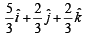
Solution.
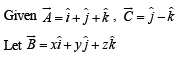
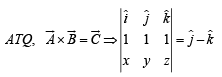
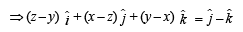
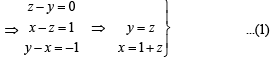
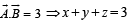
Using equations (1) and (2) we get
1 + z + z + z = 3
⇒ z = 2/3 ⇒ y = 2/3, x =5/3
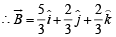
Q. 8. If the vectors 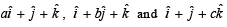 (a ≠ b ≠ c ≠ 1) are coplanar, then the value of
(a ≠ b ≠ c ≠ 1) are coplanar, then the value of 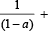
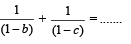 (1987 - 2 Marks)
(1987 - 2 Marks)
Ans. 1
Solution. Given that the vectors 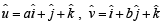 and
and 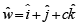 where a ≠ b ≠ c ≠ 1 are coplanar
where a ≠ b ≠ c ≠ 1 are coplanar
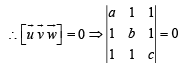
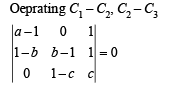
Taking (1 – a), (1 – b), (1 – c) common from R1, R2 and R3 respectively.
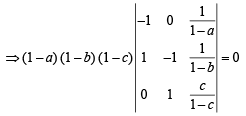
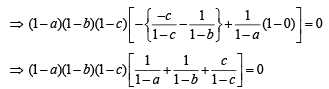
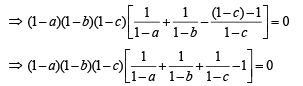
But a ≠ b ≠ c ≠ 1 (given)
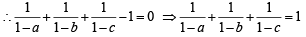
Q. 9. 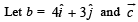 be two vectors perpendicular to each other in the xy-plane. All vectors in the same plane having projections 1 and 2 along
be two vectors perpendicular to each other in the xy-plane. All vectors in the same plane having projections 1 and 2 along 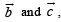 respectively,, are given by ........ (1987 - 2 Marks)
respectively,, are given by ........ (1987 - 2 Marks)
Ans. 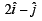
Solution.
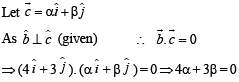
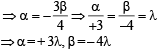 ...(1)
...(1)
Now, let 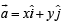 be the required vectors.
be the required vectors.
Then as per question
Projection of 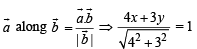
⇒ 4x + 3y = 5 ..(2)
Also, projection of 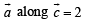
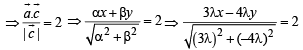
⇒ 3λx – 4λy = 10λ
⇒ 3x – 4y = 10 ...(3)
Solving (2) and (3), we get x = 2, y = – 1
∴ The required vector is 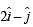
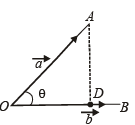
Q. 10. The components of a vector 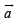 along and perpendicular to a non-zero vector
along and perpendicular to a non-zero vector 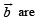 ..........and .......respectively.. (1988 - 2 Marks)
..........and .......respectively.. (1988 - 2 Marks)
Ans. 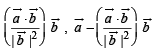
Solution. Component of 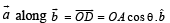
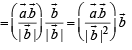
Component of 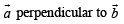
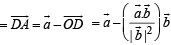
Q. 11. Given that 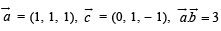 and
and  (1991 - 2 Marks)
(1991 - 2 Marks)
Ans. 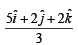
Solution.
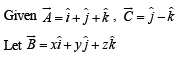
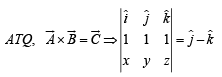
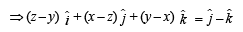
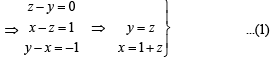
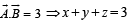
Using equations (1) and (2) we get
1 + z + z + z = 3
⇒ z = 2/3 ⇒ y = 2/3, x =5/3
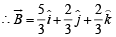
Q. 12. A unit vector coplanar with 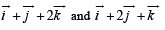 and perpendicular to
and perpendicular to 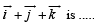 (1992 - 2 Marks)
(1992 - 2 Marks)
Ans. 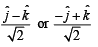
Solution. Let 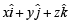 be a unit vector, coplanar with
be a unit vector, coplanar with 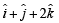 and
and 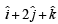 and also perpendicular to
and also perpendicular to 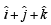
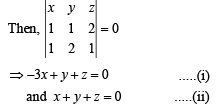
Solving the above by cross multiplication method, we get
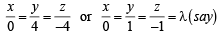
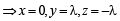
As 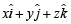 is a unit vector, therefore
is a unit vector, therefore
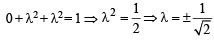
∴ The required vector is 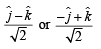
Q. 13. A unit vector perpendicular to the plane determined by the points P(1, – 1, 2) Q(2, 0, –1) and R(0, 2, 1) is ....... (1994 - 2 Marks)
Ans. 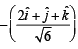
Solution. We have position vectors of points 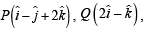
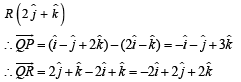
Now any vector perpendicular to the plane formed by pts
PQR is given by 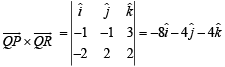
∴ Unit vector normal to plane 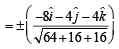
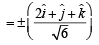
Q. 14. A nonzero vector 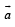 is parallel to the line of intersection of the plane determined by the vectors
is parallel to the line of intersection of the plane determined by the vectors  and the plane determined by the vectors
and the plane determined by the vectors 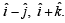 The angle between
The angle between 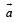 and the vector
and the vector 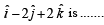 (1996 - 2 Marks)
(1996 - 2 Marks)
Ans. 
Solution. Eqn of plane containing vectors 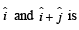
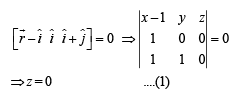
Similarly, eqn of plane containing vectors 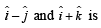
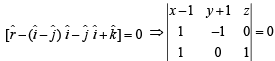
⇒ (x – 1) (–1 – 0) – (y + 1) (1 – 0) + z (0 + 1) = 0
⇒ – x + 1 – y – 1 + z = 0
⇒ x + y – z = 0 ....(2)
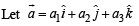
Since 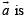 parallel to (1) and (2)
parallel to (1) and (2)
a3 = 0 and a1 + a2 – a3 = 0 ⇒ a1 = – a2 , a3 = 0
∴ a vector in direction of 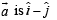
Now if θ is the angle between 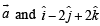 then
then
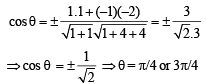
Q. 15. If 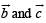 are any two non-collinear unit vectors and
are any two non-collinear unit vectors and 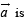 any vector, then
any vector, then 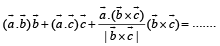 (1996 - 2 Marks)
(1996 - 2 Marks)
Ans. 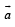
Solution. Let us consider 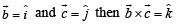
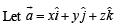
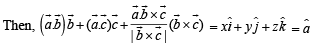
Q. 16. Let OA = a, OB = 10 a + 2b and OC = b where O, A and C are non-collinear points. Let p denote the area of the quadrilateral OABC, and let q denote the area of the parallelogram with OA and OC as adjacent sides. If p = kq, then k = ....... (1997 - 2 Marks)
Ans. 6
Solution. q = area of parallelogram with 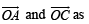
adjacent sides 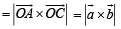
and p = area of quadrilateral OABC
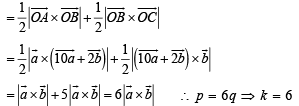
|
347 docs|185 tests
|
FAQs on Fill in the Blanks: Vector Algebra and Three Dimensional Geometry - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What are the basic operations in vector algebra? |  |
| 2. How do you find the magnitude of a vector? |  |
| 3. What is the significance of the dot product of two vectors? |  |
| 4. How is the cross product of two vectors calculated? |  |
| 5. How is three-dimensional geometry related to vector algebra? |  |
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|

















