Finding Maxima and Minima using Derivatives | Physics for JEE Main & Advanced PDF Download

Imagine you're on a roller coaster of numbers, and your goal is to find the highest and lowest points of the ride – the thrilling highs and comforting lows. Welcome to the world of Maxima and Minima! Just like figuring out the tallest hill or the deepest valley on your roller coaster adventure, in math, we're going to discover the peaks (Maxima) and valleys (Minima) of equations.

How to Find Maxima or Minima?

Where is a function at a high or low point? Calculus can help!
A maximum is a high point and a minimum is a low point:

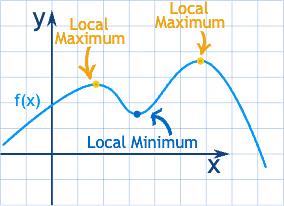Maxima and Minima

In a smoothly changing function a maximum or minimum is always where the function flattens out (except for a saddle point). Where does it flatten out?  Where the slope is zero. The Derivative tells us! 

To find the maxima or minima of a function using differentiation, you can follow these rules and steps:

• Identify the function: Let the given function be f(x).
• Take the first derivative f′(x): Find the derivative of the function with respect to x.
• Set f′(x) equal to zero: Solve the equation f′(x)=0 to find critical points.
• Find the second derivative f′′(x): Take the derivative of  f′(x).
• Analyze the sign of f′′(x):
• If f′′(x)>0 at a critical point, it indicates a local minimum.
• If f′′(x)<0 at a critical point, it indicates a local maximum.
• Evaluate the function at critical points: Substitute the critical points into the original function to find the corresponding y-coordinates.
• Interpret the results: Based on the sign of f′′(x), determine whether each critical point corresponds to a local minimum, local maximum, or neither.

Examples for Maxima and Minima

1. Let's understand this with the help of an example:
f(x)=2x²−8x+5
Identify the quadratic function: f(x)=2x²−8x+5
Take the derivative of the function: f'(x)=4x−8
Set the derivative equal to zero and solve for x: 4x−8=0; 4x=8 ; x=2
The critical point is x=2.

• To determine if it's a maximum or minimum, check the sign of the second derivative: f′′(x)=4
• Since f′′(x)>0, the function has a local minimum at x=2.
• Find the corresponding y-coordinate by substituting x=2 into the original function: 
• 2(2)2−8(2)+5  = 9
  f(2)=9

So, by using differentiation, we found that the quadratic function f(x)=2x²−8x+5 has a local minimum at x=2 with a corresponding y-coordinate of 9. 

2. Now Let's take another example to understand something more interesting:
y = x³ − 6x² + 12x − 5

The derivative is:
y' = 3x² − 12x + 12
To find the critical points: y'=0
3x² − 12x + 12=0
x= 2
Is it maxima or minima?
y''=6x-12
y''(2)=6(2)-12=0
If y''(x)=0, then this test fails.