First & Second Order Reactions | Physical Chemistry PDF Download

First-Order Reaction

A chemical reaction that has a reaction rate that is linearly dependent on the concentration of just one reactant is known as a first-order reaction. To put it another way, a first-order reaction is a type of chemical reaction in which the rate of the reaction is altered as a direct result of a change in the concentration of just one of the reactants.

Examples of First-Order Reaction

Aspirin hydrolysis and the combination of t-butyl bromide with water to produce t-butanol are two examples of first-order reactions. The hydrolysis of the anticancer medication cisplatin is another process that displays apparent first-order kinetics.

• Ammonium nitrite in aqueous solution breaks down:   NH₄NO₂ → N₂ + 2H₂O
• Ethane hydrogenation: C₂H₄ + H₂ → C₂H₆

Consider the following elementary reaction
A  → P
If the reaction is first order with respect to [A], the rate law expression is

k is rate constant

If t = 0, the initial concentration is [A]0 and the concentration at t = t, is [A], then integrating yields

[A] = [A]₀ e^–kt…(i)
or …(ii)

Using this idea, the concentration of product with time for this first-order reaction is :

[P] + [A] = [A]₀
[P] = [A]₀ – [A]
[P] = [A]₀ – [A]₀ e^–kt 
[P] = [A]₀ (1 – e^–kt) ….(iii)

Graph representation of first order reaction

[A] = [A]₀ e^–kt

Plot of concentration vs time.

ln [A] = –kt + ln [A]₀

Plot of log [A] vs time

If the graph is linear and it has a downward slope, then the reaction must be of the first order.

Half-Life of a First-Order Reaction (t_1/2)

The amount of time needed to lower the reactant concentration to 50% of its initial value is known as the half-time or half-life of a first-order reaction. Its symbol is t_1/2.

We are aware that for first-order reaction,

when t = t_1/2; then

ln 2 = kt_1/2

693

Characteristics of First-order Reaction

• The rate of the reaction is not inversely proportional to the reactant concentration.
• The rate of the reaction is proportional to the square of the reactant concentration.
• The square root of the reactant concentration determines the rate of the reaction.
• The rate of reaction is proportional to the reactant’s concentration’s natural logarithm.
• The concentration of the reactant and the rate of the reaction directly correlates.
• The rate of the reaction also increases by four times when the concentration of A is four times higher. In general, the rate of the reaction increases by n times for every n-fold increase in reactant concentration.
• The first-order reaction’s half-life, which measures how long it takes for half the reactant to react, is concentration-independent. This indicates that the first-order reaction’s half-life is constant.

Problem. The half life for the first order decomposition of N₂O₅ is 2.05 x 10⁴ s. How long will it take for a sample of N₂O₅ to decay to 60% of its initial value?

Sol. We know that,

The time at which the sample has decayed to 60% of its initial value then

T = 1.51 x 10⁴ s

Problem. Find the t_3/4 i.e. 3/4 life time of first order reaction.

Sol. Integrated rate law expression is

 

when t = t_3/4 than

then,

ln 4 = kt_3/4

Second-Order Reaction

A second-order reaction is a chemical reaction where the rate of the reaction is proportional to the square of the concentration of one reactant or the product of the concentrations of two reactants. 

The rate of these reactions can be generalized as follows:

r = k[A]^x[B]^y

Where the sum of x and y (which corresponds to the order of the chemical reaction in question) equals two.

Examples of Second Order Reactions

A few examples of second-order reactions are given below:

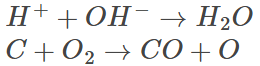
 The two examples given above are the second-order reactions depending on the concentration of two separate first-order reactants.

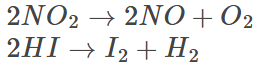
 These reactions involve one second-order reactant yielding the product.

Consider the following elementary reaction,

If the reaction is second order with respect to [A], the rate law expression is rate =

k is rate constant

 

⇒

If t = 0, the initial concentration is [A]₀ and the concentration at t = t, is [A], then integration yields

 
…(i)

The concentration of product with time for second-order reaction

 

or
then
…(ii)

Graph representation of second-order reaction

Y = mx + C

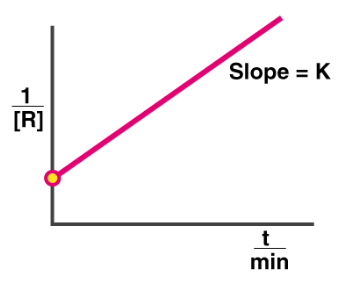Plot of concentration vs time 

Half-Life of a Second-Order Reaction (t_1/2)

when t = t_1/2 then

⇒  

Half Life of First and Second order reaction

Characteristics of Second-Order Reaction

• The reaction rate is directly proportional to the square of the reactant concentration in single-reactant second-order reactions.
• The reaction rate is proportional to the product of the concentrations of two reactants in bimolecular reactions.
• The reciprocal of the reactant concentration determines the progress of the reaction over time.
• The concentration of the reactant and the time taken for the reaction are inversely correlated.
• The rate constant ($\mathrm{<br\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">}k$k) for a second-order reaction has units of M⁻¹s⁻¹.
• The half-life decreases as the initial concentration increases.
• A plot of $\frac{1}{/[}\backslash frac\{1\}\{[A]\}$ versus time gives a straight line with a positive slope equal to $\mathrm{<br\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">}k$k.
• Doubling the reactant concentration increases the rate of the reaction by four times in single-reactant second-order reactions.
• The reaction slows down significantly as the concentration of the reactant decreases over time.

Problem. The decomposition of a compound follows second-order kinetics with a rate constant of $k\; =\; 0.050\; \backslash ,\; \backslash text\{M\}^\{-1\}\backslash text\{s\}^\{-1\}$k=0.050M⁻¹s⁻¹. If the initial concentration of the compound is $\hspace{0.17em}M0.10\; \backslash ,\; \backslash text\{M\}$0.10M, how long will it take for the concentration to decrease to 0.025M?

Sol. The decomposition of a compound follows second-order kinetics with k=0.050M⁻¹s⁻¹ Initial concentration $\hspace{0.17em}M[A]\_0\; =\; 0.10\; \backslash ,\; \backslash text\{M\}$[A]₀=0.10M, and final concentration $\left[A\right]=0.025$M.

Using the second-order integrated rate law:

Substitute the values:

$t=\frac{1}{0.050}(\frac{1}{0.025}-\frac{1}{0.10})t\; =\; \backslash frac\{1\}\{0.050\}\; \backslash left(\; \backslash frac\{1\}\{0.025\}\; -\; \backslash frac\{1\}\{0.10\}\; \backslash right)$

Simplify:

$t=$20(40−10), $\hspace{0.17em}st\; =\; 20\; \backslash times\; 30\; =\; 600\; \backslash ,\; \backslash text\{s\}$t=20×30=600s

t=600s.

Problem. A reaction is known to follow second-order kinetics. The initial concentration of the reactant is $\hspace{0.17em}M0.200\; \backslash ,\; \backslash text\{M\}$0.200M, and the rate constant is k=0.050M⁻¹s⁻¹. Calculate the half-life of the reaction.

Sol. 

Initial concentration [A]₀=0.200M, rate constant k=0.050M⁻¹s⁻¹.

The half-life for a second-order reaction is:

$t\mathrm{<sub\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 13px\; !important;\; letter-spacing:\; inherit;\; color:\; black">1</sub>}$_/2=

Substitute the values:

$t\mathrm{<sub\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 13px\; !important;\; letter-spacing:\; inherit;\; color:\; black">1</sub>}$_/2=
$t\mathrm{<sub\; style="font-size:\; 12px\; !important">1</sub>}$_/2=10.010=100 s

$\hspace{0.17em}st\_\{1/2\}\; =\; 333.33\; \backslash ,\; \backslash text\{s\}$t_1/2= 100 s.

Pseudo First-Order Reaction

Pseudo-first-order reactions are those that are not of first-order but approximate or seem to be of first-order due to higher concentrations of the reactant(s) than other reactants. It is possible to define the order of a chemical reaction as the product of the powers of the reactant concentrations in the rate law expression. 

Depending on the concentration of the reactants, reactions can be classified as first-order, second-order, pseudo-first-order, etc. Because a second-order reaction requires simultaneous measurement of both of its reactants, it can be challenging to understand.

Additional challenges may appear because, for instance, precise concentrations of each reactant are required in order to calculate the reaction rate. This may result in a high cost for the experiment if one or both of the required reactants are expensive.  We can employ the pseudo-1st-order reaction, which entails treating a 2nd-order reaction like a 1st-order reaction, to avoid more difficult, expensive experiments and calculations.

Second-order reactions involve two different reactants A and B, as follows

Assuming that the reaction is first order in both A and B, the reaction rate is

If t = 0 then the initial concentration are [A]₀ & [B]₀ and the concentration at t = t, are [A] & [B].

The loss of reactant i.e. the formation of product is equal to

[A]₀ – [A] = [B]₀ – [B] = [P]
[B]₀ – [A]₀ + [A] = [B]
then

⇒

the integration yield

let Δ = [B]₀ – [A]
The solution to the integral involving [A] is given by

Using this solution to the integral, the integrated rate law expression becomes

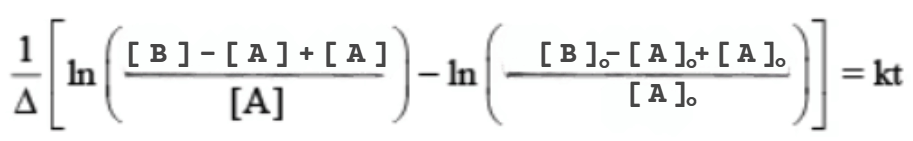
n^th order reaction where n ≥ 2 

An nth-order reaction may be represented as

the rate law is,

where k is rate constant for nth order reaction

⇒

If at t = 0, the initial concentration is [A]₀ and the concentration at t = t, is [A], then integration yields

Let

…(1)

Half lifetime of nth order reaction (t_1/2 )

Where t = t_1/2 then

 

 …(2)

i.e.  …(3)

Thus we can say that t_1/2 of the reaction is inversely proportional to the initial concentration of reactant, except first-order reaction.

So, for a first-order reaction (n = 1), t_1/2 is independent on [A]₀ for a second-order reaction (n = 2), t_1/2 is dependent on [A]₀

for a nth order reaction 

Note : For the elementary reaction, the order of reaction is equal to the molecularity of the reaction.