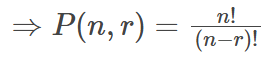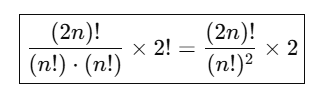When choosing three different flavors from five available options, what mathematical concept is used when the order of selection matters?

Permutations are used when the order of selection matters.

True or False: Combinations apply when the order of selection is significant.

False. Combinations apply when the order of selection does not matter.

In the case where repetition of objects is not allowed, the number of permutations is calculated using which expression?

N(E) = n × (n - 1) × (n - 2) × ... × (n - (r - 1))

The number of permutations of 'n' distinct objects is given by ___ .

N!

In permutations, the order of objects is ___, while in combinations, it is ___.

Important; not important

What is the formula for calculating the number of permutations of 'r' objects from 'n' objects?

Fill in the blank: The number of ways to choose 'r' objects from 'n' objects is given by the formula ___, and to find permutations, this must be multiplied by ___ for each combination.

^NC_r; r!

What does the Multiplication Principle state regarding the performance of operations?

Operations combine in m×n ways.

• First operation has m options.

• Second operation has n options.

• Total combinations are m×n ways.

The number of permutations of n different things taken r at a time, allowing repetitions, is given by ___?

• Since repetitions are allowed, each of the r positions can be filled in n ways.

• So, total number of ways = n×n×⋯×n = n^r (r times).

True or False: The number of permutations of n things taken all at a time, when m specified things never come together, is equal to n! - m! × (n - m + 1)!

True

What is the formula for dividing 2n different elements into two groups of n objects each when the order of the groups is important?

The coefficient of xⁿ⁻ʳ in the expansion of (1 + x + x² + … + x^(k-1))ʳ represents what?

It represents the number of ways of dividing n identical things among r persons such that each person gets 1, 2, 3, …, or k things.

What is the formula for calculating the number of circular permutations of n different things taken all at a time when clockwise and anti-clockwise orders are not considered different?

(when clockwise and anti-clockwise are considered the same)

Fill in the blank: When fixing the position of one object, the number of circular permutations of the remaining objects is ___!

(n - 1)!