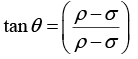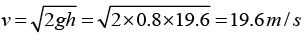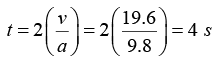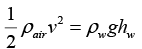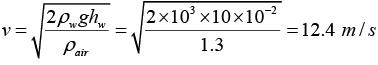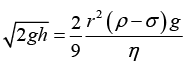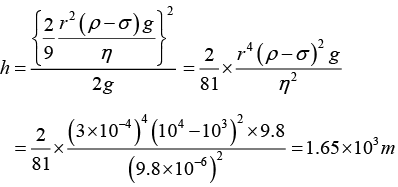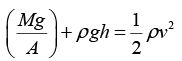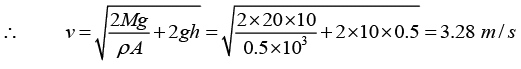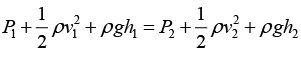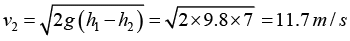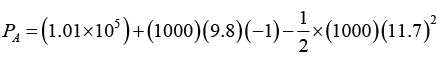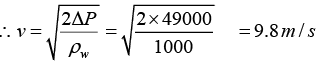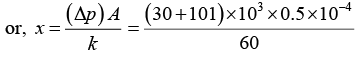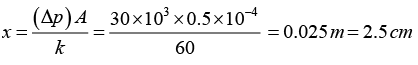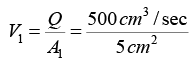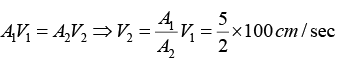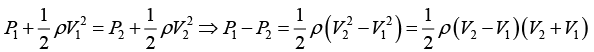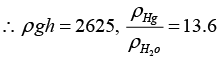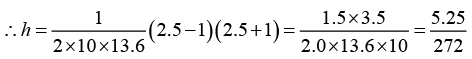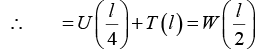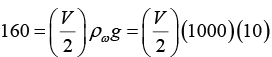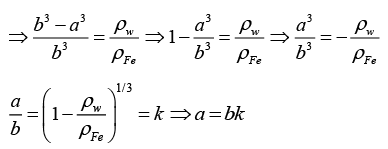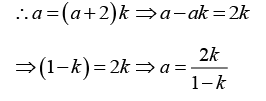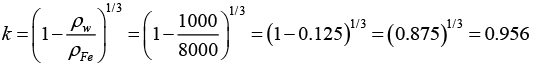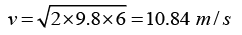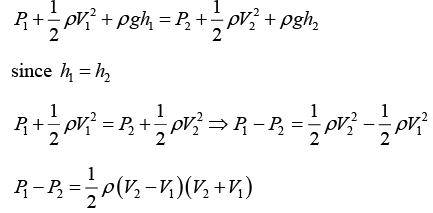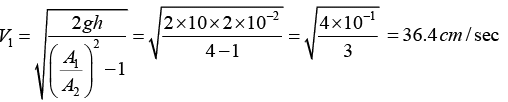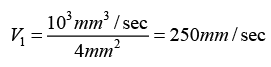Fluid Mechanics: Assignment Part - 2 | Mechanics & General Properties of Matter - Physics PDF Download
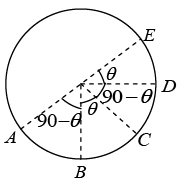
Q.1. A small uniform tube is benit into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities are σ(ρ > s) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.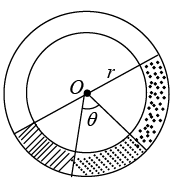
hAB = r - cos(90 - θ) = r - r sin θ
hBC = r - r cos θ
hCD = r sin(90 - θ) = r cos θ
hDE = r sin θ
Writing pressure equation between points A and E we have
pA + (r - r sin θ) - ρg(r - r cos θ) ρg - (r cos θ)(σ) g - (r sin θ) σg = PEBut pA = pE
Solving this equation we get
Q.2. A solid ball of density half that of water falls freely under gravity from a height of 19.6 m and then enters water. Upto what depth will the ball go and how much time will it take to come again to the water surface? Neglect air resistance and viscosity effects in water
(Take g = 9.8 m/s2)
Let ρ be the density of ball and 2r the density of water.
Net retardation inside the water,(V = volume of ball)
Hence, the ball will go upto the same depth 19.6 m below the water surface.Further, time taken by the ball to come back to water surface is,
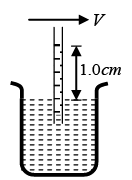
Q.3. When air of density 1.3 kg/m3 flows across the top of the tube shown in the accompanying figure, water rises in the tube to a height of 1.0 cm. What is the speed of the air?
Q.4. A spherical ball of radius 3.0 x 10-4 m and density 104 kg/m3 falls freely under gravity through a distance h before entering a tank of water. If after entering the water the velocity of the ball does not change, find h. Viscosity of water is 9.8 x 10-6 N-s/m2.
Before entering the water the velocity of ball is
. If after entering the water this velocity does not change then this value should be equal to the terminal velocity.
Therefore,
Q.5. The area of cross-section of a large tank is 0.5 m2. It has an opening near the bottom having area of cross-section 1 cm 2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. (Take g = 10 m/s2)
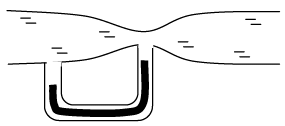
Q.6. The U - tube acts as a water siphon. The bend in the tube is 1m above the water surface. The tube outlet is 7m below the water surface. The water issues from the bottom of the siphon as a free jet at atmospheric pressure. Determine the speed of the free jet and the minimum absolute pressure of the water in the bend.
Given atmospheric pressure = 1.01x105 N/m2, g = 9.8m/s2 and density of water = 103 kg/m3 .
(a) Applying Bernoulli’s equation between points (1) and (2)
Since, area of reservoir >> area of pipe
v1 » 0,
also P1 = P2 = atmosphere pressure
So,
(b) The minimum pressure in the bend will be at A . Therefore, applying Bernoulli’s equation between (1) and ( A)
Therefore, substituting the values, we have
= 2.27 x 104 N/m2
Q.7. A tank having a small circular hole contains oil on top of water. It is immersed in a large tank of the same oil. Water flows through the hole. What is the velocity of this flow initially? When the flow stops, what would be the position of the oil-water interface in the tank from the bottom. The specific gravity of oil is 0.5.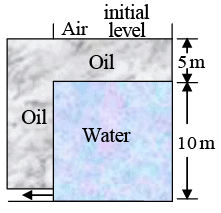
(a) Δp = h(ρw - ρ0) g = (10)(1000 - 500)9.8
= 49000 N/m2
Now, Δp = 1/2 ρwv2
(b) The flow will stop when,
(10 + 5)ρ0g = 5ρ0g + hρwg
10ρ0 = hρw
∴ h = 10 x 500/1000 = 5 m
i.e., flow will stop when the water-oil interface is at a height of 5.0 m.
Q.8. The pressure gauge shown in figure has a spring for which k = 60N/m and the area of the piston is 0.50cm2. It right end is connected to a closed container of gas at a gauge pressure of 30kPα. How far will the spring be compressed if the region containing the spring is
(a) in vacuum and
(b) open to the atmosphere? Atmosphere pressure is 101kPα.
(a) Force from left hand side = Force from right hand side
∴ kx = ΔpA
= 0.109 m or 10.9 cm
(b)
Q.9. Water flows through the tube shown in figure. The areas of cross-section of the wide and the narrow portions of the tube are 5 cm2 and 2 cm2 respectively. The rate of flow of water through the tube is 500 cm3/s . Find the difference of mercury levels in the U-tube.
Q = 500 cm3/sec
Q = A1V1 = A2V2V1 = 100 cm/sec V1 = 1m/sec
Also
V = 250 cm/sec V2 = 2.5m/sec
P1 - P2 = 1/2 x 1000 x (2.5-1)(2.5 + 1) = 2625 Pα
Now P1 = PC = PD = PE + ρgh = P2 + ρgh
PC = P1 + ρgh1, PE = P2 + ρgh2, PC - PE = P1 - P2 + ρgh
Now P1 = PC = PD = PE + ρgh = P2 ρgh ⇒ P1 - P2 = ρgh
1/2 ρw(V2 - V1)(V2 + V1) = ρHggh
h = 0.0193 m = 1.93 cm
Q.10. A uniform rod AB,4m long and weighing 12kg, is supported at end A, with a 6 kg lead weight at B . The rod floats as shown in figure with one-half of its length submerged. The buoyant force on the lead mass is negligible as it is of negligible volume. Find the tension in the cord and the total volume of the rod.
T + U = 60 + W (i)
∑(Moments ) about O = 0
or, U + 4T = 2W (ii)
W = 120N (iii)
Solving these three equations we get T = 20 N and U = 160 N
Now,
∴ v = 32 x 10-3m3
Q.11. A cubical box is to be constructed with iron sheets 1 mm in thickness, What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron = 8000 kg / m3 and density of water 1000 kg/m3 .
(mass of iron) g = (mass of displaced liquid) g
⇒ ρFe(b3 - a3)g = ρwb3g
where
∴ α = 2 x 0.956/1-0.956 = 43.45 mm and b = 45.45 mm
Q.12. A fresh water on a reservoir is 10m deep. A horizontal pipe 4.0cm in diameter passes through the reservoir 6.0m below the water surface as shown in figure. A plug secures the pipe opening.
(a) Find the friction between the plug and pipe wall.
(b) The plug is removed. What volume of water flows out of the pipe in 1h ? Assume area of reservoir to be too large.
(a) Force of friction = pressure difference on the sides of the plug ´ area of cross section of the plug (ρgh) A = (10)3(9.8)(6.0)(π)(2x10-2)2 = 73.9 N
(b) Assuming the area of the reservoir to be too large,
Velocity of efflux,= constant
∴
Q.13. Water flows through a horizontal tube as shown in figure. If the difference of heights of water column in the vertical tubes is 2 cm and the areas of cross-section at A and B are 4 cm2 and 2 cm2 respectively, find the rate of flow of water across any section.
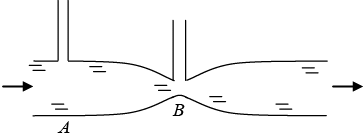
Equation of continuity
A1V1 = A2V2
Bernauli equation:
Also P1 - P2 = ρgh
∴ ρgh = 1/2 ρ(V2 - V1)(V2 + V1)(V2 - V1) (V2 + V1) = 2gh
at
∴ Q = A1V1 = 4 x 10-4 x 0.364 = 145.6 cm3/sec
Q.14. Water flows through a horizontal tube of variable cross-section (figure 1). The area of cross-section at A and B are 4 mm2 and 2 mm2 respectively. If 1 cc of water enters per second through A , find (a) the speed of water at A , (b) the speed of water at B and (c) the pressure difference PA - PB.
(a) Equation of continuity A1V1 = A2V2
Given Q = A1V1 = 1cm/sec = 1cm3/sec
(b) Since A1V1 = A2V2 ⇒ V2= 500mm/sec
∴ V1 = 250 mm/sec, V2 = 500 mm/sec or V1 = 25 cm/sec, V2 = 50 cm/sec or V1 = 0.25 m/sec, V2 = 0.5m/sec
(c) According to Bernauli’s equation:
P1 - P2 = 1000/2(0.75)(0.25) = 93.75 Pα
Q.15. A solid sphere of mass m = 2kg and density r = 500kg/m3 is held stationary relative to a tank filled with water. The tank is accelerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank.
(Density of water = 1000 kg/m3, g= 10 m/s2)
(a) Up thrust – Weight - T= mα
∴ T= Up thrust - Weight - mα
= (2/500) (1000)(10+2) - 20 - 4 = 48 - 20 - 4 = 24 N
(b) Downward force T suddenly becomes zero.
Therefore, α = (Up thrust – Weight)/m = 48-20/2 = 14m/s2
∴ Acceleration w.r.t. tank
= 14 - 2 = 12m/s2
|
61 videos|23 docs|25 tests
|
FAQs on Fluid Mechanics: Assignment Part - 2 - Mechanics & General Properties of Matter - Physics
| 1. What are the basic principles of fluid mechanics? |  |
| 2. What is the difference between laminar and turbulent flow? |  |
| 3. How is Bernoulli's principle applied in fluid mechanics? |  |
| 4. What is the concept of viscosity in fluid mechanics? |  |
| 5. How is fluid mechanics applied in real-life situations? |  |