Formula Sheet and Example - Matrices and Determinants | Business Mathematics and Statistics - B Com PDF Download
Addition and Subtraction of Matrices
- A + B = B + A
- (A + B) + C = A + (B + C)
- k (A + B) = kA + kB
Multiplication of matrices
- AB ≠ BA
- (AB) C = A (BC)
- Distributive law
A (B + C) = AB + AC
(A + B) C = AC + BC - Multiplicative identity
For a square matrix A
AI = IA = A
Proerties of transpose of matrix
- (AT) T = A
- (kA)T = kAT
- (A + B)T = AT + BT
- (AB)T = BT AT
Symmetric and Skew Symmetric matrices
- Symmetric Matrix - If AT = A
- Skew - symmetric Matrix - If AT = A
Note: In a skew matrix, diagonal elements are always 0. - For any square matrix A,
(A + AT) is a symmetric matrix
(A − AT) is a skew-symmetric matrix
Inverse of a matrix
For a square matrix A, if
AB = BA = I
Then, B is the inverse of A
i.e. B = A−1
We will find inverse of a matrix by
- Elementary transformation
- Using adjoint
Properties of Inverse
- For a matrix A,
A−1 is unique, i.e., there is only one inverse of a matrix - (A −1) −1 = A
- (𝑘 𝐴)−1 = 1/𝑘 𝐴 −1
Note: This is different from
(kA)T = k AT - (A -1) T = (AT)-1
- (A+B)-1 = A-1 + B-1
- (𝐴𝐵)−1 = 𝐵−1 𝐴−1
Important things to note in Determinants
- Determinant of Identity matrix = 1
det (I) = 1 - |AT | = |A|
- |AB| = |A| |B|
- |A −1 | = 1/|𝐴|
- |kA| = kn |A| where n is order of matrix
- Similarly,
|−A| = |−1 × A|
= (−1)n × |A| - (adj A) A = A (adj) = |A|I
- Deteminant of adj A
|"adj A| = |A | 𝑛−1
where n is the order of determinant
Number multiplied to matrix and determinant

Problems and Solution.
Problems 1.
Let 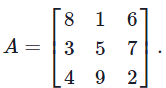 Notice that A contains every integer from 1 to 9 and that the sums of each row, column, and diagonal of A are equal. Such a grid is sometimes called a magic square. Compute the determinant of A.
Notice that A contains every integer from 1 to 9 and that the sums of each row, column, and diagonal of A are equal. Such a grid is sometimes called a magic square. Compute the determinant of A.
Solution. We compute using the first row cofactor expansion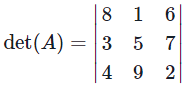
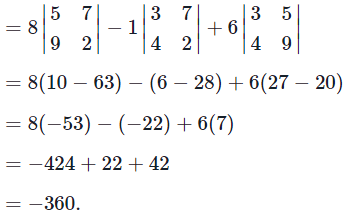
Problems 2. Let A and B be n×n matrices, where n is an integer greater than 1. Is it true that det(A+B) = det(A) + det(B)?
If so, then give a proof. If not, then give a counterexample.
Solution.
We claim that the statement is false.
As a counterexample, consider the matrices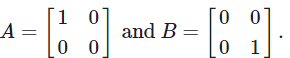
Then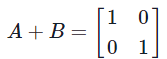
and we have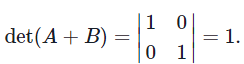
On the other hand, the determinants of A and B are
det(A) = 0 and det(B) = 0,
and hence det(A) + det(B) = 0 ≠ 1 = det(A+B).
Therefore, the statement is false and in general we have
det(A+B) ≠ det(A) + det(B).
Problems 3. Let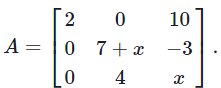 Find all values of x such that A is invertible.
Find all values of x such that A is invertible.
Solution.A matrix is invertible if and only if its determinant is non-zero.
So we first calculate the determinant of the matrix A.
By the first column cofactor expansion, we have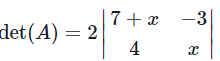
= 2((7 + x)x − (−3)4) = 2(x2 + 7x + 12)
= 2(x + 3)(x + 4).
Thus the determinant of A is zero if and only if x = −3 or x = −4.
Therefore the matrix A is invertible for all x except x = −3 and x = −4.
Problems 4. Let 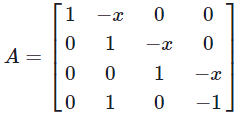 be a 4×4 matrix. Find all values of x so that the matrix A is singular.
be a 4×4 matrix. Find all values of x so that the matrix A is singular.
Solution. We use the fact that a matrix is singular if and only if the determinant of the matrix is zero. We compute the determinant of A as follows.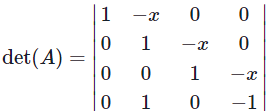
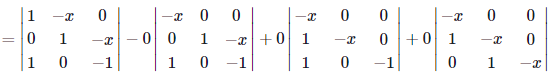
by the first column cofactor expansion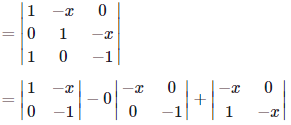
by the first column cofactor expansion
= −1 + x2.
Therefore we have det(A) = x2−1. Thus det(A)=0 if and only if x = ±1.
We conclude that the matrix A is singular if and only if x = ±1.
Problems 5. Find all the values of x so that the following matrix A is a singular matrix.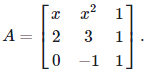
Solution. Note that a matrix is singular if and only if its determinant is zero.
So we compute the determinant of the matrix A as follows.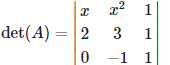
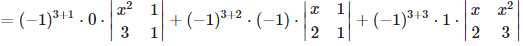
by the third row cofactor expansion
= 0+(x−2)+(3x−2x2)
= −2x2+4x−2.
Thus the determinant of A is zero if
det(A) = −2x2+4x−2=0,
equivalently,
x2−2x+1=(x−1)2=0.
Thus, the determinant of the matrix A is zero if and only if x = 1.
Hence the matrix A is singular if and only if x = 1.
Problems 6. Find the value(s) of h for which the following set of vectors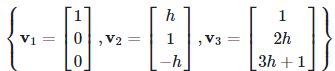 is linearly independent.
is linearly independent.
Solution. Let us consider the linear combination
x1v1 + x2v2 + x3v3 = 0. (*)
If this homogeneous system has only zero solution x1 = x2 = x3 =0, then the vectors v1,v2,v3 are linearly independent.
We reduce the augmented matrix for the system as follows.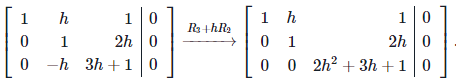
From this, we see that the homogeneous system (*) has only the zero solution if and only if
2h2 + 3h + 1 ≠ 0.
Since we have
2h2+3h+1=(2h+1)(h+1),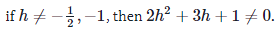
In summary, the vectors v1,v2,v3 are linearly independent for any h except 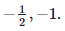
Problems 7. Let A be a 3×3 matrix.
Let x,y,z are linearly independent 3-dimensional vectors. Suppose that we have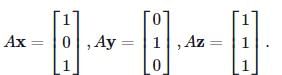
Then find the value of the determinant of the matrix A.
Solution. Let B be the 3×3 matrix whose columns are the vectors x,y,z, that is,
B = [xyz].
Then we have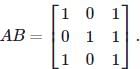
Then we have
(If two rows are equal, then the determinant is zero. Or you may compute the determinant by the second column cofactor expansion.)
Note that the column vectors of B are linearly independent, and hence B is nonsingular matrix. Thus the det(B)≠0.
Therefore the determinant of A must be zero.
Problems 8. Given any constants a,b,c where a≠0, find all values of x such that the matrix A is invertible if 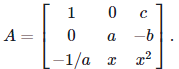
Solution.
We know that A is invertible precisely when det(A)≠0. We therefore compute, by expanding along the first row,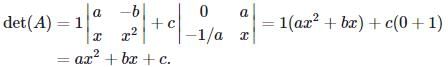
Thus det(A)≠0 when ax2+bx+c≠0. We know by the quadratic formula that ax2+bx+c=0 precisely when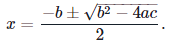
Therefore, A is invertible so long as x satisfies both of the following inequalities: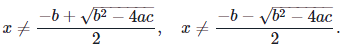
|
124 videos|176 docs
|
FAQs on Formula Sheet and Example - Matrices and Determinants - Business Mathematics and Statistics - B Com
| 1. What is a matrix? |  |
| 2. How are matrices added or subtracted? |  |
| 3. What is the determinant of a matrix? |  |
| 4. How is the determinant of a 2x2 matrix calculated? |  |
| 5. How do you find the inverse of a matrix? |  |






















