Formulas & Solved Examples: Exponents & Roots | Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET PDF Download
| Table of contents |

|
| Exponents: |

|
| Formulas of Exponents |

|
| Roots |

|
| Formulas of Roots |

|
| Solved Questions on Exponents and Roots |

|
Exponents:
Exponents are a "shortcut" method of showing a number that was multiplied by itself several times.
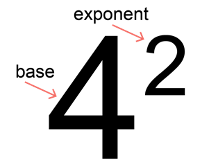
- For instance, number a multiplied n times can be written as an, where a represents the base, the number that is multiplied by itself n times and n represents the exponent.
- The exponent indicates how many times to multiply the base,a, by itself.
Formulas of Exponents
1. Exponents one and zero:
a0=1 Any nonzero number to the power of 0 is 1.
For example 50=1 and (−3)0=1
Note: the case of 0^0 is not tested on the GMAT.
a1=a Any number to the power 1 is itself.
2. Powers of zero:
If the exponent is positive, the power of zero is zero: 0n=0, where n>0.
If the exponent is negative, the power of zero (0n, where n<0) is undefined because division by zero is implied.
3. Powers of one:
1n=1 The integer powers of one are one.
4. Negative powers:
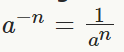
Important: you cannot rise 0 to a negative power because you get division by 0, which is NOT allowed. For example, 0−1=1/0=undefined
5. Powers of minus one:
If n is an even integer, then (−1)n = 1
If n is an odd integer, then (−1)n = −1.
6. Operations involving the same exponents:
Keep the exponent, multiply or divide the bases

7. Operations involving the same bases:
Keep the base, add or subtract the exponent (add for multiplication, subtract for division)
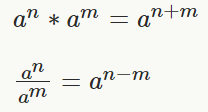
8. Fraction as power:
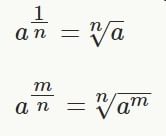
Roots
Roots (or radicals) are the "opposite" operation of applying exponents. For instance x2=16 and square root of 16=4.
Formulas of Roots
Solved Questions on Exponents and Roots
Section - 1
Simplify the following expressions by combining like terms. If the base is a number, leave the answer in exponential form (i.e. 23, not 8).
Ques 1. x5 x x3
Ans: x5 x x3 = x(5+3) = x8
Ques 2: 76 x 79
Ans: 76 x 79 = 7(6+9) = 715
Ques 3: 55/55
Ans: 5(5-3) = 52
Ques 4: (a3)2
Ans: (a2)3 = a(3x2) = a6
Ques 5: 4-2 x 45
Ans: 4-2 x 45 = 4(-2+5) = 43
Ques 6: (-3)a/(-3)2
Ans: (-3)(a-2)
Ques 7: (3)2-3
Ans: (32)-3 = 3(2 x -3) = 3-6
Ques 8: 114/11x
Ans: 11(4-x)
Ques 9: x2 x x3 x x5
Ans: x2 x x3 x x5 = X (2 + 3 + 5) = x10
Ques 10: (52)x
Ans: (52)x=5(2 * x)= 52x
Section - 2
Ques 11: 34 x 32 x 3
Ans: 34 x 32 x 3
= 3(4 + 2 + 1) = 37
Ques 12: x5 x x6 /x2
Ans: x(5+6- 2) = x9
Ques 13: 56 x 54x / 54
Ans: 5(6+ 4x—4) = 54x+2
Ques 14: y7 x y8 x y-6
Ans: y7 x y8 x y-6
= y(7 + 8 + (-6))
= y9
Ques 15: x4/x-3
Ans: x(4-(-3)) = x7
Ques 16: z5 x z-3/z-8
Ans: z(5+(-3)-(-8))= z10
Ques 17: 32x x 36x/3-3y
Ans: 3(2x+6x-(-3y)) = 38x+3y
Ques 18: (x2)6 x x3
Ans: x(2 x 6 + 3) = x(12+3) = x15
Ques 19: (z6)x x z3x
Ans: z(6 * x+3x) = z(6x+3x) = z9x
Ques 20: 53 x (54)y/(5y)3
Ans: 5(3+(4xy)-(y x 3)) = 5(3+4y-3y)= 5y+3
Section - 3
Ques 21: Compute the sum.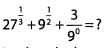
Ans:
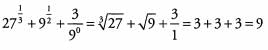
Ques 22: Which of the following has the lowest value?
(A) (-3)4
(B) -33
(C) (-3)-3
(D) (-2)3
(E) 2-6
Ans: We are looking for the answer with the lowest value, so we can focus only on answers that are negative as these answers have lower values than any positive answers.
(A) (-3)4 will result in a positive number because 4 is an even power.
(B) -33 = -(3)3 = -27
The exponent is done before multiplication (by -1) because of the order of operations.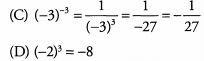
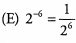
The value of this expression is positive.
-2 7 has the lowest value of the three answer choices that result in negative numbers. The correct answer is (B).
Ques 23: Compute the sum. 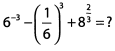
Ans: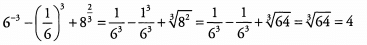
The first two terms in the expression are in fact the same. Because these terms are equal, when the second is subtracted from the first they cancel out leaving only the third term.
Ques 24: Which of the following is equal to (2/5)-3?
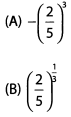
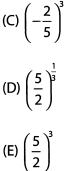
Ans: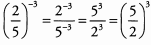
The correct answer is (E).
Note: when a problem asks you to find a different or more simplified version of the same thing, check your work against the answer choices frequently to ensure that you don’t simplify or manipulate too far.
Ques 25: Which of the following has a value less than 1 ? (Select all that apply)
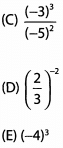
Ans: We are looking for values less than 1 so any expressions with negative values, zero itself, or values between 0 and 1 will work.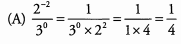
Dividing a smaller positive number by a larger positive number will result in a number less than 1.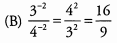
Dividing a larger positive number by a smaller positive number will result in a number greater than 1.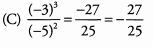
This answer is negative; therefore, it is less than 1.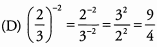
Dividing a larger positive number by a smaller positive number will result in a number greater than 1.
(E) (-4)3 = -64
This answer is negative; therefore, it is less than 1.
Section - 4
Simplify the following expressions by finding common bases.
Ques 26: 83 x 26
Ans: 83 x 26 = (23)3 x 26 = 29 x 26 = 215
Ques 27: 492 x 77
Ans: (72)2 x 77 = 74 x 77 = 711
Ques 28: 254 x 1253
Ans: (52)4 x (53)3 = 58 x 59 = 517
Ques 29: 9-2 x 272
Ans: (32)-2 x (33)2 = 3-4 x 36 = 32
Section - 5
Simplify the following expressions by pulling out as many common factors as possible.
Ques 31: 63 + 33 = (A) 35 (B) 39 (C) 2(33)
Ans: Begin by breaking 6 down into its prime factors.
63 + 33 =
(2 x 3)3 + 33 =
(23) (33) + 33
Now each term contains (33). Factor it out.
(23)(33) + 33 =
33(23 + 1) =
33(9) =
33(32) = 35
We have a match. The answer is A.
Ques 32: 813 + 274 = (A) 37(2) (B) 312(2) (C) 314
Ans: Both bases are powers of 3. Rewrite the bases and combine.
813 + 274 =
(34)3 + (33)4 =
312 + 312 =
312(1 + 1) =
312(2)
We have a match. The answer is B.
Ques 33: 152- 52 = (A) 52(2) (B) 5223 (C) 5232
Ans: Begin by breaking 15 down into its prime factors.
152 - 52 =
(3 x 5)2 - 52 =
(32)(52) - 52
Now both terms contain 52. Factor it out.
(32)(52) - 52 =
52(32 - 1) =
52(9 - 1) =
52(8)
We still don’t have a match, but we can break 8 down into its prime factors.
52(8) =
52(23)
We have a match. The answer is B.
Section 6
Ques 34: 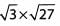
Ans: 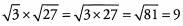
Ques 35: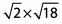
Ans: 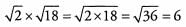
Ques 36: 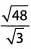
Ans:
Ques 37:
Ans:
Ques 38: 
Ans: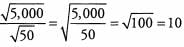
Ques 39: 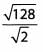
Ans:
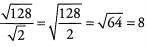
Ques 40: 
Ans:
Ques 41: 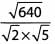
Ans:
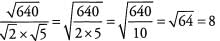
Ques 42: 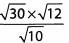
Ans: 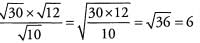
Section - 7
Simplify the following roots. Not every answer will be an integer.
Ques 43: √32
Ans: 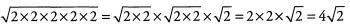
Ques 44: √24
Ans: 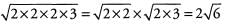
Ques 45: √180
Ans: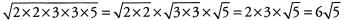
Ques 46: √490
Ans: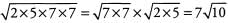
Ques 47: √450
Ans: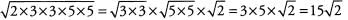
Ques 48: √135
Ans: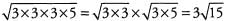
Ques 49: √224
Ans: 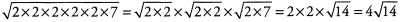
Ques 50: √343
Ans: 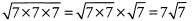
Section - 8
Simplify the following roots. You will be able to completely eliminate the root in every question. Ex- press answers as integers.
Ques 51: 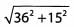
Ans: Pull out the greatest common factor of 362 and 152, namely 32, to give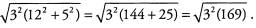 Both 32 and 169 are perfect squares (169 = 132), so
Both 32 and 169 are perfect squares (169 = 132), so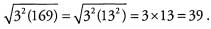
Ques 52: 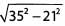
Ans: Pull out the greatest common factor of 352 and 212, namely 72, to give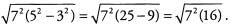 Both 72 and 16 are perfect squares (16 = 42), so
Both 72 and 16 are perfect squares (16 = 42), so
Ques 53: 
Ans: Pull out the greatest common factor of 56 and 57, namely 56, to give Both 62 and 56 are perfect squares (56= 53 x 53), so
Both 62 and 56 are perfect squares (56= 53 x 53), so
Ques 54: 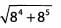
Ans: Pull out the greatest common factor of 84 and 85, namely 84, to give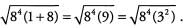
Both 84 and 32 are perfect squares (84 = 82 x 82), so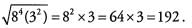
Ques 55: 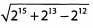
Ans: Pull out the greatest common factor of 215, 213, and 212, namely 212, to give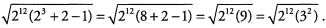
Both 212 and 32 are perfect squares
(212 = 26 x 26), 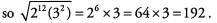
Ques 56: 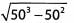
Ans: Pull out the greatest common factor of 503 and 502, namely 502, to give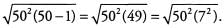
Both 502 and 72 are perfect squares, so 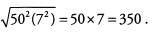
|
82 videos|273 docs|69 tests
|
FAQs on Formulas & Solved Examples: Exponents & Roots - Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET
| 1. What is the formula for calculating the value of an exponent? |  |
| 2. How do you simplify expressions with exponents? |  |
| 3. What is the formula for calculating the square root of a number? |  |
| 4. How do you simplify expressions with roots? |  |
| 5. How do you solve equations involving exponents and roots? |  |
















