Fourier Series: Assignment | Mathematical Methods - Physics PDF Download
Q.1. Expand 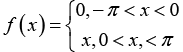 in trigonometric Fourier series. Draw three periods and use it to derive the following relations.
in trigonometric Fourier series. Draw three periods and use it to derive the following relations.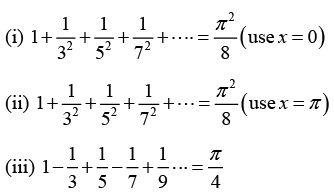
Thus the trigonometric Fourier series of the given function is
The graph of the function is shown in the figure(i) At x = 0 , the Fourier series converges to
(ii) At x = π we have
(iii) we have at x = π/2Thus
Hence
Q.2. Expand the given function in Fourier Series 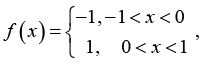 and hence find the value of
and hence find the value of 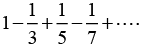
Given Function
Here, 2l = 2 ⇒ l = 1
Thus, bn = 4/nπ for odd n.= 0 for even n.
Hence the Fourier Series of the given function is
Q.3. The function shown in the graph is plotted for one period. Sketch it over three periods and use the graph to find the Fourier series of the function shown.
The function shown in the graph is plotted for one period. Sketch it over three periods and use the graph to find the Fourier series of the function shown.
f (x) = -(x + π), -π < x < 0
x, 0 < x < π
Hence
= 0 for even n
Thus, bn = 2/n for odd n
= 0 for even n
Thus the Fourier series of the given function is
Q.4. Expand the given function in Fourier Series 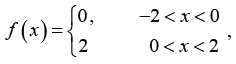 and hence find the value of
and hence find the value of 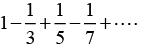
Thus Fourier series is
At x = 1, f (x) = 2
Q.5. Find the Fourier series of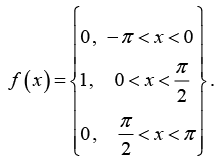
Now,for n = 1, 5, 9, 13
for 3, 7,11,15
andfor even n.
Thus, an = 1/nπ for n = 1, 5, 9, 13for n 3, 7,11,15
We can write the general formula forfor even n and
for odd n.
Now,
for 2, 6,10,14....
= +1 for n = 4, 8,12,16 ......
= 0 for odd n
Hence bn = 2/nπ for n = 2, 6,10,14....
= 0 for n = 4, 8, 12, 16 ....= 1/nπ for odd n.
We can write the general formula for even nThus bn = 1/nπ , for odd n.
Thus the Fourier series of the given function is
Q.6. Expand the given function in Fourier Series 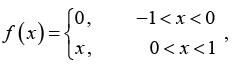 and hence find the value of
and hence find the value of 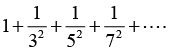
The given function is
Here, 2l = 2 ⇒ l = 1
for odd n and an a = for even n.
Thus the Fourier Series of the given function isPutting x = 0 gives
Q.7. Find the Fourier series of f (x) = x2 , 0 < x < 2π
The given function is f (x) = x2 , 0 < x < 2π
Thus, bn = -4π/n for all n.
Thus the Fourier series of the given function is
Q.8. Expand the given function in Fourier Series f(x) = π sinπx, 0 < x < 1 and hence find the value of 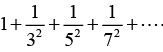
Here, 2l = 1 ⇒ l = 1/2
For all n
Thus the Fourier Series of the given function is given byAt x = 0 , the function is discontinuous and the fourier series converges to

Q.9. Find the Fourier series of
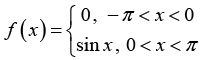
The given function is
We know that
We see that this formula holds for n ≠ 1.
Hence we directly calculate
Now let us evaluate an using equation (I)
when n is odd, (n + 1) is even and (n - 1) is even. Thus for odd n,
When n is even (n + 1) and (n - 1) are odd, hence
Thus an = 0 for odd n
Now we have
We see that we cannot calculate b1 using this formula.
Let us evaluate b1 directly
Let us evaluate other bn ’s using equation (ii)
Thus bn = 0 for all n.Hence the Fourier Series of the given function is
In the expanded form
Q.10. Expand the given functions in Fourier Series f(x) = ex , 0 < x < 2 and hence find the value of 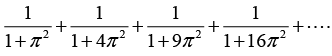
f(x) = ex , 0 < x < 2
Hence,
Thus the Fourier Series of the given function is
In the expanded form we can writeAt x = 0, the function is discontinuous and the Fourier series converges to the average of its left hand and right hand limit.
Thus , at x = 0
|
78 videos|18 docs|24 tests
|
FAQs on Fourier Series: Assignment - Mathematical Methods - Physics
| 1. What is a Fourier series? |  |
| 2. How is a Fourier series calculated? |  |
| 3. What are the applications of Fourier series? |  |
| 4. Can any periodic function be represented by a Fourier series? |  |
| 5. Are there any limitations or drawbacks of using Fourier series? |  |









































 for n = 1, 5, 9, 13
for n = 1, 5, 9, 13 for 3, 7,11,15
for 3, 7,11,15 for even n.
for even n. for n 3, 7,11,15
for n 3, 7,11,15 for even n and
for even n and  for odd n.
for odd n.


 for 2, 6,10,14....
for 2, 6,10,14....







 for odd n and an a = for even n.
for odd n and an a = for even n.









 Here, 2l = 1 ⇒ l = 1/2
Here, 2l = 1 ⇒ l = 1/2




































































