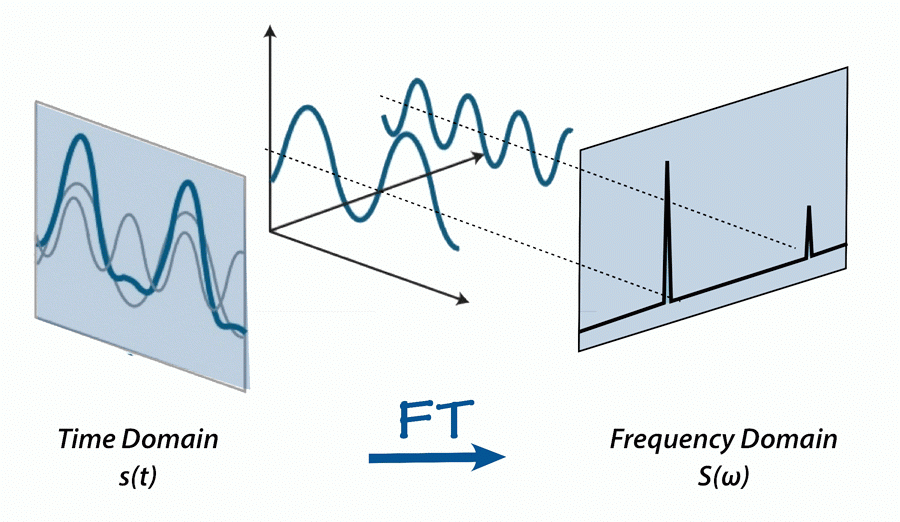
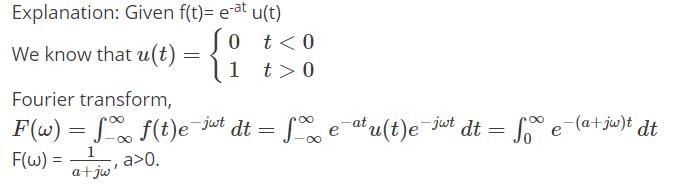Fourier Transform & Its Properties | Signals and Systems - Electrical Engineering (EE) PDF Download
What is Fourier Transform?
- The Fourier transform is nothing but, it is a generalization of the Fourier series representation of functions.
- The advantage of Fourier transform over the Fourier series is that the Fourier transform can be used for a larger class of functions which are not necessarily periodic.
Fourier Transform Properties
- Since the transform is essential to the understanding of several exercises, so here we will explain some basic Fourier transform concepts.
- Recall the definition of the Fourier series expansion for a periodic function u(t). If u(t + T) = u(t), then
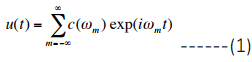
where ωm = 2πm/T so that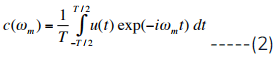
- If u(t) is a function of time it is natural to call ωm an angular frequency and to refer to C(ωm) as the amplitude of u(t) at frequency ωm. Together, the c(ωm) comprise the frequency spectrum of u(t).
- Computing the frequency spectrum for a sine or square wave of period T is fairly simple. For the sine wave, there are only two non-zero coefficients:
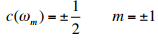
- Since the odd fact that the formalism requires both positive and negative frequencies. The spectrum of the square wave is slightly more complicated:
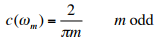
- The interesting feature here is that the rapid rise and fall of the square wave leads to spectral components at high frequency, as demonstrated in figure below.
- Building up a square wave from Fourier series components. Each graph is a plot of Sn, the sum of the first n terms in the series expansion, for increasing values of n.

- For many purposes, a knowledge of the C(ωm) may be more useful than knowing u(t) itself. It is therefore desirable to extend the idea of a frequency spectrum to non-periodic functions, for example single pulses or finite wave trains. This can be done by replacing the sum of Eqn. 1 by an integral, giving
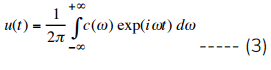
and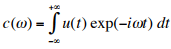 .........(4)
.........(4) - where ω is now a continuous variable. The complex function c(ω) is called the Fourier transform of u(t) and is again the amplitude of u(t) at frequency ω.
- This can be understand as the transform of exp(iωot) is a delta function, δ(ω-ωo). This says that the spectrum of exp(iωot) has a large amplitude only at ω=ωo, which seems reasonable since the function is periodic with angular frequency ωo.
Example: Consider another specific and important example. Consider the “rect” function (“rect” for “rectangle”) defined by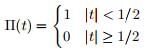
- The Fourier transform of a pulse centered at t = 0 ; is simply
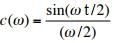
- Note that a short pulse (small t) leads to a significant c(ω) over a wide frequency range, while a long pulse (large t) implies c(ω) decreases quickly with frequency.
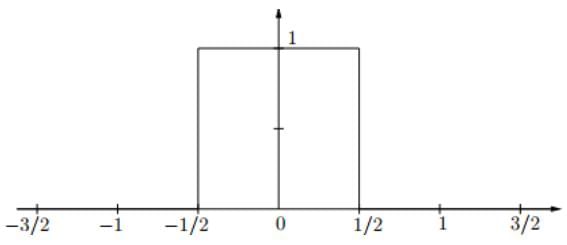
- Π(t) is even — centered at the origin — and has width 1. Later we’ll consider shifted and scaled versions. Here You can think of Π(t) as modeling a switch that is on for one second and off for the rest of the time. Π is also called, variously, the top hat function (because of its graph), the indicator function, or the characteristic function for the interval (−1/2, 1/2).
- While we have defined Π(±1/2) = 0, other common conventions are either to have Π(±1/2) = 1 orΠ(±1/2) = 1/2.
- Some people don’t define Π at ±1/2 at all, leaving two holes in the domain. Here we don’t want to get dragged into this dispute. It almost never matters, though for some purposes the choice Π(±1/2) = 1/2 makes the most sense.
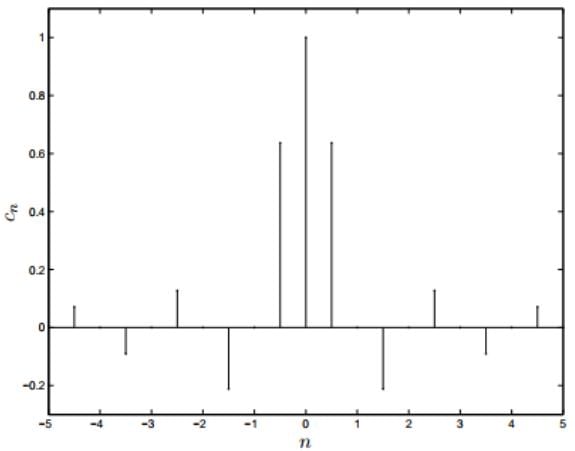
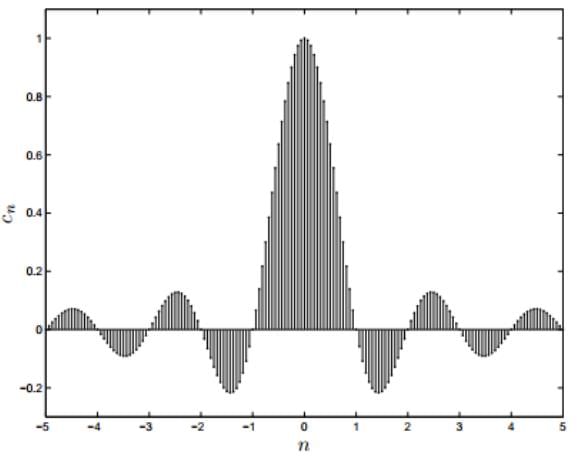
- In the above two plots of the Fourier coefficients of periodized rectangle functions with periods 2, 4, and 16, respectively. Because the function is real and even, in each case the Fourier coefficients are real, so these are plots of the actual coefficients, not their square magnitudes.
- Since general function f(t) of period T the Fourier series has the form
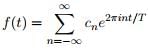 Here the frequencies are 0, ±1/T, ±2/T, . . ..Points in the spectrum and are spaced 1/T apart,indeed in the pictures above the spectrum is getting more tightly packed as the period T increases.
Here the frequencies are 0, ±1/T, ±2/T, . . ..Points in the spectrum and are spaced 1/T apart,indeed in the pictures above the spectrum is getting more tightly packed as the period T increases. - The n-th Fourier coefficient is given by:

- We can calculate this Fourier coefficient for Π(t):
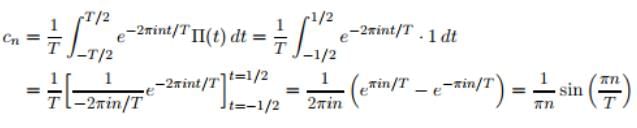
- Here although the spectrum is indexed by n the points in the spectrum are n/T (n = 0, ±1, ±2,...), and it’s more easy to think about the “spectral information” (the value of cn) as a transform of Π evaluated at the points n/T.
- so we can write this, provisionally, as
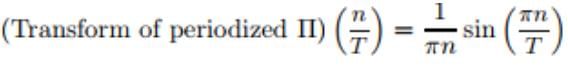
- To compensate for this we scale up by T, that is, we consider instead
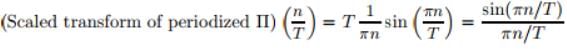
- Now, if T is large so we can replace the closely packed discrete points n/T by a continuous variable, say s, so that with s = n/T we would then write, approximately,
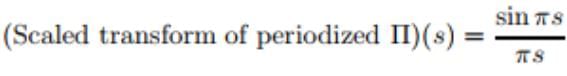
- This procedure look like in terms of the integral formula Simply as
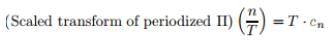

- If we Consider as T → ∞ having the effect of replacing the discrete variable n/T by the continuous variable s, as well as pushing the limits of integration to ±∞, then we may write for the (limiting) transform of Π the integral expression such as
- So the integral becomes:
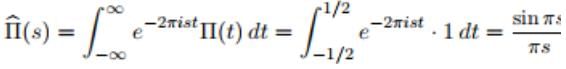
- So finally the graph is obtained now certainly see the continuous curve that the plots of the discrete, scaled Fourier coefficients are shadowing.
- The above function (sin πx)/πx comes up so often in this subject that it’s given a name, sinc.
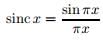
- It pronounced as "Sink" ⇒ sinc0 = 1 ; Hence by virtue of the famous limit
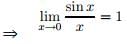
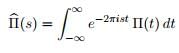
- We now define the Fourier transform of a function f(t) as:
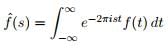
Recovering f(t) from f(s)
- Again suppose f(t) is zero outside some interval and periodize it to have (large) period T. We expand f(t) in a Fourier series:
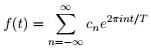
- The Fourier coefficients can be written via the Fourier transform of f evaluated at the points sn = n/T
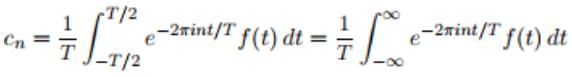
- Here we can extend the limits to ±∞ since f(t) is zero outside of [−T/2,T/2]
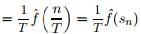
- So finally f(t) becomes
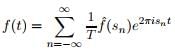
So that we have recovered f(t) from f(s).
➢ The Inverse Fourier Transform
- The integral we’ve just come up with can stand on its own as a “transform”, and so we define the inverse Fourier transform of a function 'g(s)' to be

Fourier Inversion Theorem
- Again here we are treating this formally for a moment withholding a discussion of conditions under which the integral makes sense. In the same way we can produced the Fourier inversion theorem. That is
this can also be written as
- The Inverse Fourier Theorem looks just like the Fourier transform except for the minus sign.
Power Spectrum of Fourier Integral
- The square magnitude |fˆ(s)|2 is called the power spectrum which is applied in communications the spectral power density or the energy spectrum.
- The relation between the energy of the signal in the time domain and the energy spectrum in the frequency domain is given by Parseval’s identity for Fourier transforms:
General Properties and Formulas
- Fourier transform pairs and duality
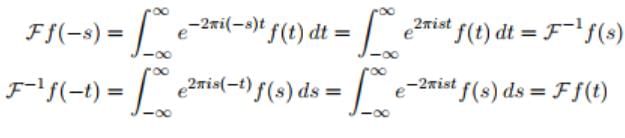
- Even and Odd Symmetries and the Fourier Transform
(i) If f(x) is an Odd Function then (Ff)− = −Ff
(ii) If f(x) is an Even Function then (Ff)− = Ff - If f(t) is real-valued then

- The shift theorem: If f(t)⇔ F(s) then f(t + b) ⇔ e2πisbF(s)
- The stretch (similarity) theorem
This is also sometimes called the Similarity Theorem because changing the variable from x to ax is a change of scale, also known as a similarity.
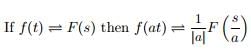
Convolution of Fourier Transform
- The convolution of two functions g(t) and f(t) is the function:
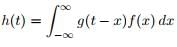
- We use the notation
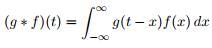
- Convolution Theorem: F(g∗f)(s) = Fg(s) Ff(s)
Frequently Asked Questions
Q.1. What is the Fourier transform?
Ans: The Fourier transform is a type of mathematical function that splits a waveform, which is a time function, into the type of frequencies that it is made of. A function’s Fourier transform is a complex-valued function denoting the complex sinusoids that contain the original function. For every frequency, the magnitude of the complex value denotes the constituent complex sinusoid’s amplitude with that frequency, and the complex value’s argument denotes the phase offset of the complex sinusoid.
Q.2. What are the main properties of Fourier transform?
Ans: The important properties of Fourier transform are duality, linear transform, modulation property, and Parseval’s theorem.
Q.3. What is the main purpose of the Fourier series?
Ans: The Fourier series is primarily used to represent a periodic signal in the form of cosine and sine waves. Specifically, it enables us to model any arbitrary periodic signal with a union of cosines and sines.
Q.4. What are the two primary types of Fourier series?
Ans: The two primary types of Fourier series are exponential series and trigonometric series.
Q.5. What is meant by the Fourier series?
Ans: A Fourier series is a precise expansion of periodic functions f(x) in terms of infinite sums of cosines and sines. This series utilises the orthogonality connection of the cosine and sine functions.
Q.6. What are the steps to solve a Fourier series?
Ans: Steps which are required for solving a Fourier series are as follows:
- Multiply the function by cosine or sine and then integrate it.
- Take n = 0, n = 1, n = 2, etc. to calculate the value of coefficients.
- In the end, add all the respective coefficients in the Fourier formula.
Q.7. Who was the first person to develop the first form of Fourier transforms?
Ans: Joseph Fourier proposed (The Analytic Theory of Heat) that any arbitrary function, whether discontinuous or continuous, can be extended into a series of sines.
Q.8. What is the connection between the Fourier transform and uncertainty principle?
Ans: Uncertainty principles point to a meta-theorem in Fourier study that describes that a non-zero function and its Fourier transform cannot be localised to arbitrary precision. Any mathematical expression which multiplies a function that shows localisation with its Fourier transform could be an uncertainty principle.
Q.9. What is the role of Fourier transform in Fourier transform spectroscopy?
Ans: In the case of spectroscopy, the Fourier transform is used in infrared (FTIR), nuclear magnetic resonance (NMR), etc. Also, the Fourier transform is used for mass spectrometry and magnetic resonance imaging (MRI).
|
41 videos|70 docs|33 tests
|