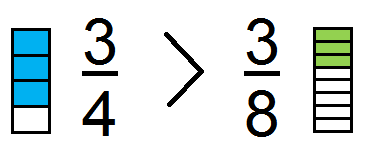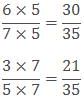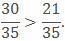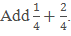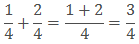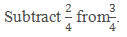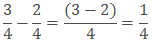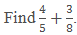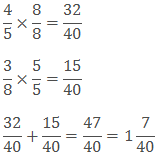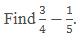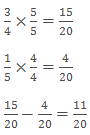Fractions Class 6 Notes Maths Chapter 7
What is Fraction?
A Fraction is a part of whole. The ‘whole’ here could be an object or the group of objects. But all the parts of the whole must be equal.
Numerator and Denominator
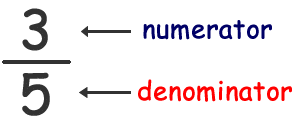
- The upper part of the fraction is called Numerator. It tells the number of parts we have.
- The lower part of the fraction is called Denominator. It tells the total parts in a whole.
- It reads as "three-fifths".
Representation of fraction on Number line
Let us understand it with the help of an example.
Example: 
Solution:
- Draw a number line. We know that 1/2 is less than 1 and greater than 0, so we have to divide the gap between two equal parts and then mark the middle point as 1/2.
- As the denominator is the whole and the numerator is the part, so we have to divide the gap between 0 and 1 in the number of parts as the denominator is given.
- For 1/3, divide into 3 equal parts.
- For 1/4, divide into 4 equal parts and so on.
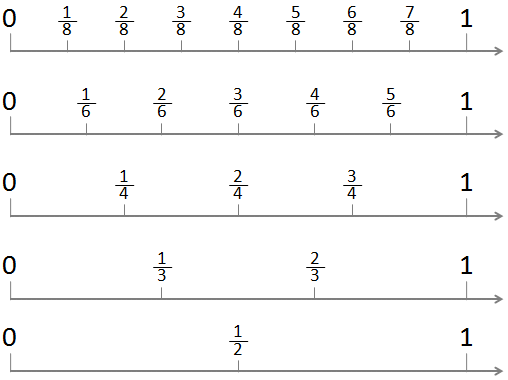
Proper Fractions
If the numerator is less than the denominator then it is called proper fraction. If we represent a proper fraction on the number line than it will always lie between 0 and 1.
Examples: 2/5, 5/8, 1/10 etc.
Improper fractions and Mixed fractions
- When the numerator is greater than the denominator then it is called Improper fraction.
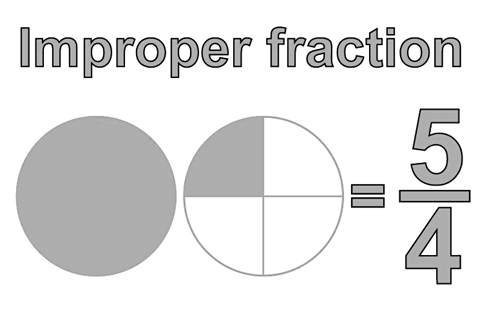
The above fraction is made by adding one whole part and one-fourth part.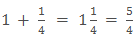
- The fraction made by the combination of whole and a part is called Mixed fraction.
Convert Mixed fraction into Improper fraction
- A mixed fraction is in the form of
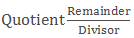
- We can convert it in the form of an improper fraction by:
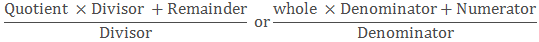
Example: 
Sol: 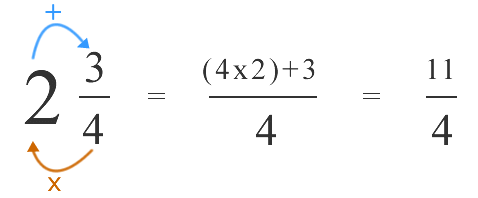
Equivalent Fractions
Equivalent fractions are those fractions which represent the same part of a whole.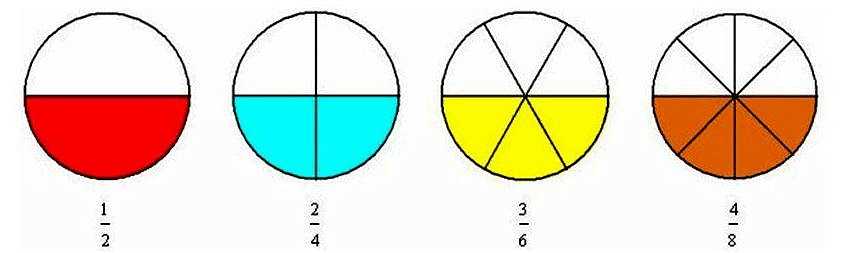
All the above images are different but equivalent fractions as they represent the same i.e. half part of a whole circle.
Finding Equivalent Fractions
1. Finding equivalent fractions
If we multiply the numerator and denominator of any fraction with the same number then we will get the equivalent fraction. There could be more than one equivalent fractions of one fraction.
Example: Find three equivalent fraction of ½.
Sol: 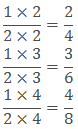
2. Dividing the same number
If we divide the numerator and denominator of any fraction with the same number then we will get the equivalent fraction.
The Simplest Form of a Fraction
If the numerator and denominator do not have any other common factor than 1 then it is said to be the simplest or lowest form of that fraction.
Example: Reduce the fraction 18/27 in the simplest form.
Sol: HCF of 18 and 27 is 9.
Hence,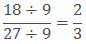
2/3 is the lowest form of 18/27.
Like Fractions and Unlike Fractions
- Fractions which have same denominators are known as Like fractions.
Example: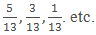
- Fractions which have different denominators are known as Unlike fractions.
Example: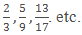
Comparing Fractions
1. Comparing like fractions
Like fractions are the fractions with the same denominator so we have to compare them with the numerator only. The fraction with greater numerator is greater.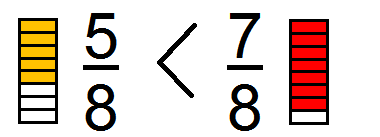
In the above example, both are divided into 8 equal parts, so the fraction with seven shaded part is greater than the 5 shaded parts.
2. Comparing unlike fractions
The fractions with different denominators are unlike fractions.
(i) Unlike fraction with the same numerator
If we have to compare the fractions with different denominator but same numerator, we have to compare with the denominator only.
In that case, the fraction with the small denominator is greater than the other.
Example:
Here the numerator is same i.e.3 so we will compare with the denominator. The fraction with small denominator i.e. ¾ is greater than the fraction with the large denominator i.e. 3/8.
(ii) Unlike fraction with different numerators
If the numerator and denominator both are different then we have to make the denominator same by finding the equivalent fraction of both the fractions then compare the fractions as like fractions. To find the equivalent fraction of both the fractions with the same denominator, we have to take the LCM of the denominator.
Example: Compare 6/7 and 3/5.
Solution: The product of 7 and 5 is 35.
So we will find the equivalent fraction of both the fractions with the denominator 35.
Now we can compare them as like fractions.
Addition and Subtraction of Fractions
1. Adding like fractions
In case of like fractions, the denominator is same so we can add them easily.
Steps to add like fractions-
Step 1: Add the numerators.
Step 2: Leave the common denominator same. (Don’t add the denominator).
Step 3: Write the answer as
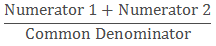
Example:
Solution:
2. Subtracting like fractions: Steps to subtract the like fractions-
Step 1: Subtract the small numerator from the bigger one.
Step 2: Leave the common denominator same.
Step 3: Write the answer as

Example:
Solution:
3. Adding unlike fraction
If we have to add the unlike fractions, first we have to find the equivalent fraction of the given fractions with the same denominator then add them.
Steps to add unlike fractions-
Step 1 : Take the LCM of the denominator of the given fractions.
Step 2: Find the equivalent fractions of both fractions with LCM as the denominator.
Step 3: Add them as the like fractions.
Example:
Solution: Take the LCM of 5 and 8, which is 40.
4. Subtracting unlike fractions
Steps to subtract unlike fractions-
Step 1: Take the LCM of the denominator of the given fractions.
Step 2: Find the equivalent fractions of both fractions with LCM as the denominator.
Step 3: Subtract them as the like fractions.
Example:
Solution: LCM of 4 and 5 is 20.
|
151 videos|223 docs|60 tests
|