Fun with Symmetry Class 4 Notes Maths Chapter 11 Free PDF
| Table of contents |

|
| Introduction |

|
| 1. Ink Design |

|
| 2. Making a paper airplane |

|
| 3. Holes and Cuts |

|
| Lines of Symmetry in Shapes |

|
| Tiles at the Tile Shop |

|
| Some Solved Examples |

|
Introduction
Have you ever noticed how a butterfly's wings look exactly the same on both sides? Or how folding a paper heart in half makes two parts that match perfectly? This perfect balance is called symmetry, and it's everywhere around us!
We see it in beautiful rangoli patterns, colourful masks, intricate bead strings, and even in the design of large buildings. In your earlier classes, you might have already played with symmetrical shapes while making crafts.
In this chapter, we're going on an exciting journey to explore the world of symmetry in more detail.
What is Symmetry?
Symmetry is like looking in a mirror! A shape or an object is considered symmetrical if you can draw an imaginary line through its center, dividing it into two halves that are exact mirror images of each other.
Think about your own body – if you imagine a line running straight down from the top of your head to your feet, your left side is very similar to your right side. This imaginary dividing line is called the Line of Symmetry or sometimes the Axis of Symmetry or Mirror Line. If you fold a symmetrical shape along its line of symmetry, the two halves will match up perfectly, covering each other exactly without any parts sticking out.
If you fold a symmetrical shape along its line of symmetry, the two halves will match up perfectly, covering each other exactly without any parts sticking out.
What do you think are all objects symmetrical?
No, some objects like the ones given below are not symmetrical. They are called non-symmetrical objects or things.
1. Ink Design
Let's create some beautiful symmetrical patterns using just paper and paint! This is a fun way to see symmetry in action.
Step 1: Take a sheet of paper and carefully fold it exactly in half. Make a nice crease along the fold.
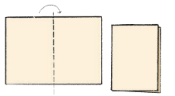
Step 2: Open the paper up. Now, sprinkle a few drops of watery paint or ink right onto the center of the fold line.

Step 3: Fold the paper back in half along the same crease, and gently press down to spread the paint evenly between the two halves.

Step 4: Carefully open the paper again. Look at the amazing design you've created!

You created a symmetrical pattern — a design where both halves match each other perfectly.
You can now find and draw the line of symmetry — the line that divides the pattern into two equal halves.
2. Making a paper airplane
Making a paper airplane is not just fun, it's also a great way to see symmetry!
Let's follow the steps shown in the pictures below to fold one.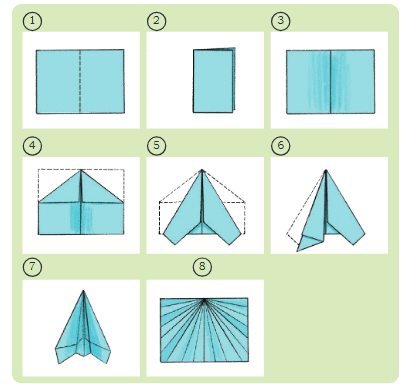
- As you fold the paper, especially in the early steps where you fold it in half lengthwise, you create a line of symmetry.
- Look closely at the plane after steps 3, 4, and 5. Can you see the line of symmetry running down the middle?
This line ensures that both sides of the airplane (the wings) are identical, which helps it fly straight and balanced.
This activity teaches us that symmetry is important for balance and function. By making a paper airplane, we learn how folding equally on both sides creates a symmetrical shape, which helps the plane fly smoothly. It shows that symmetrical designs are more stable and work better, and helps us understand symmetry not just in shapes, but in real-life objects too.
3. Holes and Cuts
Mini made some cool shapes by folding and cutting paper.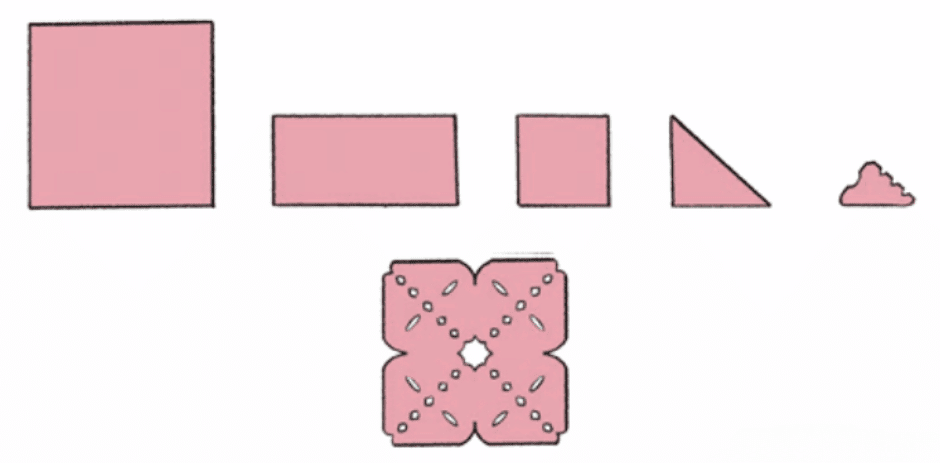 Different shapes made by Mini
Different shapes made by Mini
Now it’s your turn to become a paper-cutting artist like Rani!
What Rani Did:
1. She took a square paper.
2. Folded it twice:
First in half from left to right.
Then in half from top to bottom.
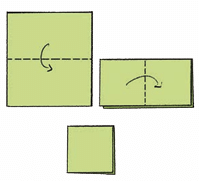
3. Then she cut out small shapes from the folded paper — at the corners and edges.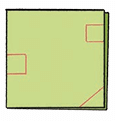
When she opened the paper, the same shape appeared on all 4 sides!
Why? Because the paper was folded — so one cut made many shapes appear!


Lines of Symmetry in Shapes
We've seen symmetry in ink blots and paper folding, but many basic geometric shapes also have lines of symmetry. Remember, a line of symmetry divides a shape into two identical halves that mirror each other.
Some shapes have one line of symmetry, some have multiple lines, and some have none at all!
One Line of Symmetry: Think of an isosceles triangle (a triangle with two equal sides) or a human face. You can usually draw one line down the middle.
Example: An isosceles triangle has only one line of symmetry.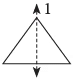
Multiple Lines of Symmetry: A square has four lines of symmetry (one vertical, one horizontal, and two diagonal). An equilateral triangle (all sides equal) has three lines of symmetry. A circle has infinite lines of symmetry – any line passing through its center will divide it into two identical semicircles!
Example: A square has four lines of symmetry.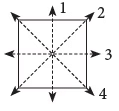
No Lines of Symmetry: A scalene triangle (all sides different lengths) or a parallelogram generally have no lines of symmetry.
Example: A scalene triangle has no line of symmetry.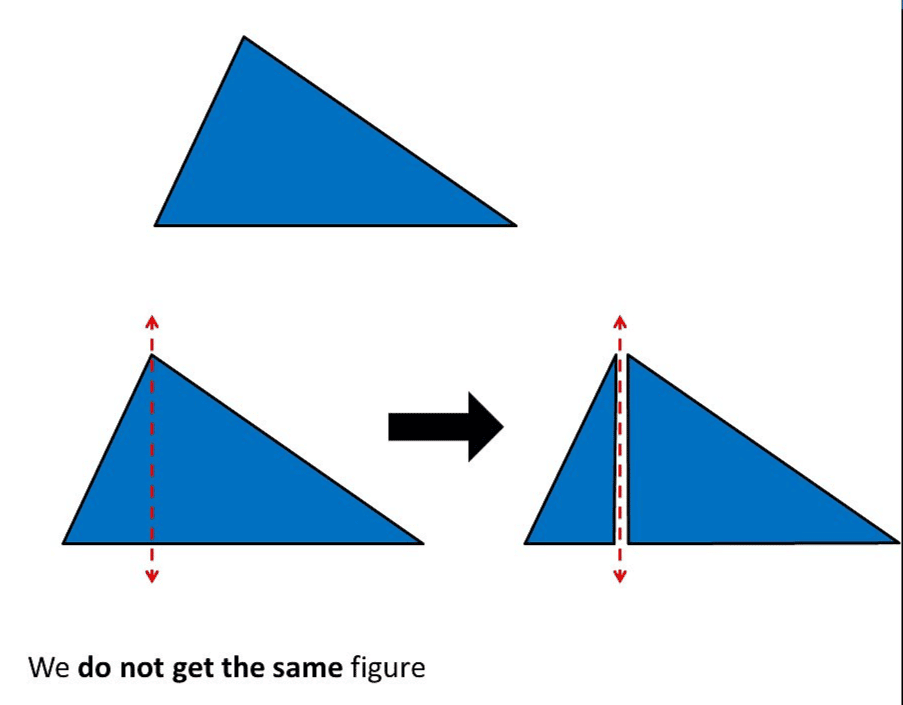
Mirror Images and Reflection
When you look into a mirror, you see your reflection. The mirror image is the reflection of the image.
We can see that a symmetrical shape can be split in half by the line of symmetry. If we put a small mirror on the dotted line, we will see the whole shape. Thus, you can see that a shape has line symmetry when one half of it is the mirror image of the other half.
 Thus, reflectional symmetry is also known as mirror symmetry.
Thus, reflectional symmetry is also known as mirror symmetry.
Look at the reflection of some numbers and letters.

Symmetry in Letters and Numbers
Here are some capital letters and numbers which have lines of symmetry.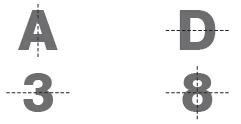
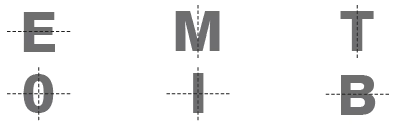 However, there are some letters and numbers which are not symmetrical.
However, there are some letters and numbers which are not symmetrical.
Geometrical Patterns Based on Symmetry
Rangoli patterns are drawn as decorations during the festival of Diwali. The pictures given here show two such patterns.
Now, look at the following patterns.
This pattern is symmetrical.
It can be folded in half, so all the lines and colours in each half fit exactly on top of each other.
Quilt patterns based on symmetry.
This pattern is not symmetrical.
When it is folded in half, some of the lines and colours do not match.
Tiles at the Tile Shop
Welcome to Bablu Chacha’s Tile Shop! In this fun and colorful topic, you will explore how to make beautiful tile patterns using different shapes.
What Are Tiles?
Tiles are small flat pieces used to decorate walls and floors. They often come in repeating patterns made using shapes. In this activity, you’ll become a tile designer and create patterns just like the ones you see in homes and shops!
Look at the Tiles
Observe the tile designs given above. You’ll see many creative tiles made from different shapes. Try to identify the shapes used — like hexagons, triangles, and squares.
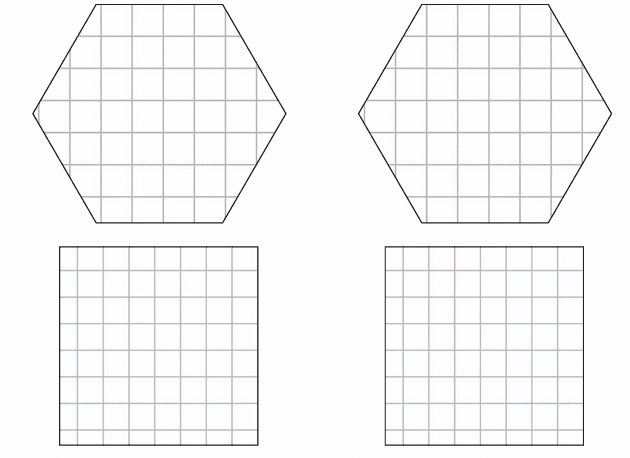
Make Your Own Tiles
Use the blank hexagon and square grids to draw your own tile patterns. You can:
Use colored pencils or a geometry kit.
Repeat shapes to create a design.
Mix and match different shapes to make it look unique.
Find the Symmetry
After designing your tile, look for lines of symmetry — if you draw a line in the middle, both sides should look the same. If they do, your tile is symmetrical!
Join Tiles Without Gaps
Use the square grids at the bottom to combine two or more tiles. Make sure the tiles fit together perfectly, with no gaps or overlaps. This is how real tile floors are made!
To Summarise:
Some Solved Examples
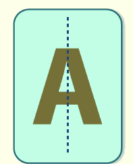
Example 1: Does the capital letter A have a line of symmetry?
Sol: Yes! If you draw a vertical line down the middle of the letter A, both sides are the same.
Example 2: Choose the shape with no line of symmetry:
Circle, Rectangle, Irregular Leaf, Square
Sol: An irregular leaf is not the same on both sides when folded — it has no symmetry.
Example 3: Raju folded a square paper and cut a triangle on the fold. When he opened it, what did he see?
Sol: He saw two identical triangles on opposite sides — a symmetrical pattern across the fold line.
|
54 videos|186 docs|14 tests
|
FAQs on Fun with Symmetry Class 4 Notes Maths Chapter 11 Free PDF
| 1. What is symmetry in designs and why is it important? |  |
| 2. How can we identify mirror images in numbers? |  |
| 3. Are there any letters in the alphabet that are symmetrical? |  |
| 4. What are lines of symmetry and how can we find them in shapes? |  |
| 5. How is symmetry used in tiles and patterns? |  |