Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Functions Toolkit
Functions Toolkit | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Introduction to Functions
What is a function?
- A function represents a set of mathematical operations that transform one set of numbers into another set.
- It can be visualized as a mathematical "machine" where specific rules are applied to input numbers to produce output numbers.
- For instance, consider a function with the rule "double the number and add 1." Here, the operations involved are "multiply by 2" and "add 1."
- When 3 is input into this function: 2 x 3 + 1 = 7
- When -4 is input: 2 x (-4) + 1 = -7
- The number input into the function is commonly termed the input, while the resulting number is referred to as the output.
What does a function look like?
- A function f can be written as f(x) = … or f : x ↦ …
- These two different types of notation mean exactly the same thing
- Other letters can be used. g, h and j are common but any letter can technically be used
- Normally, a new letter will be used to define a new function in a question
- For example, the function with the rule “triple the number and subtract 4” would be written
- f(x) = 3x − 4 or f: x ↦ 3x − 4.
- In such cases, x would be the input and straight f open parentheses x close parentheses would be the output
- Sometimes functions don’t have names like f and are just written as y = …
- eg. y = 3x − 4.
How does a function work?
- A function has an input (x) and an output (f(x) or y).
- Whatever is inside the bracket with f replaces x in the function.
- This value is the input.
- If the input is known, the output can be calculated.
- For example, given f(x) = 2x + 1:
- f(3) = 2 ⋅ 3 + 1 = 7
- f(−4) = 2 ⋅ (−4) + 1 = −7
- f(a) = 2a + 1
- If the output is known, an equation can be formed to find the input.
- For example, given f(x) = 2x + 1:
- If f(x) = 15, then the equation 2x + 1 = 15 can be formed.
- Solving this equation gives an input of 7.
What is a mapping diagram?
- A mapping diagram illustrates how an 'input' from one set corresponds to an 'output' in another set.
- For example, a mapping diagram for the function x + 3 where x ≥ 3 could be shown as:

Domain & Range
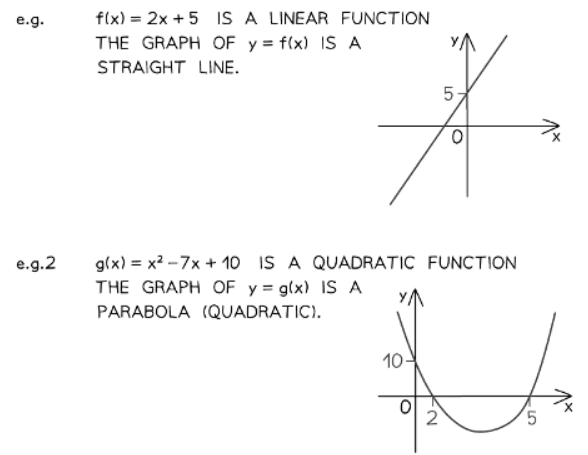
How are functions related to graphs?
- Functions are graphically represented on x and y axes.
- The x-axis values serve as the inputs.
- The y-axis values represent the outputs.
- To plot the graph, substitute f(x) with y =
What is the domain of a function?
- The domain of a function is the set of all inputs that the function is allowed to take
- Domains can be described in words
- they must refer to x
- not y or f(x)
- you can use "not equal to" ≠ if needed
- you can use inequality signs if needed
- they must refer to x
- Examples of domains are below:
- f(x) = 3x + 2 takes any x value
- the domain is "all values of x"
- f(x) = 1/x takes any x value except 0 (you cannot divide by 0)
- the domain is "all values of x except 0", or simply "x ≠ 0"
- f(x) = √x takes any x value that are not negative (you cannot square root a negative)
- the domain is "x ≥ 0"
- f(x) = x2 takes any x value (negative x values are fine as inputs)
- the domain is "all values of x"
- f(x) = 3x + 2 takes any x value
- Some domains are restricted by choice
- f(x) = 3x + 2 with the domain 0 < x < 5
- This question wants to concentrate on that domain only (even though bigger domains exist)
- f(x) = 3x + 2 with the domain 0 < x < 5
- Some domains must exclude certain values (or sets of values)
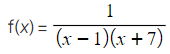 must exclude x = 1 and x = -7 from any domain
must exclude x = 1 and x = -7 from any domain- These two inputs make the function undefined (dividing by zero)
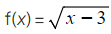 must exclude x < 3 from any domain
must exclude x < 3 from any domain- Any input in x < 3 leads to square-rooting a negative

What is the range of a function?
- The range of a function is the set of all outputs that the function gives out
- Ranges can be described in words
- they must refer to f(x)
- not x or y
- you can use "not equal to" ≠ if needed
- you can use inequality signs if needed
- they must refer to f(x)
- Ranges are influenced by domains
- Examples of ranges are below:
- f(x) = 3x + 2 with domain x > 0
- The range is "f(x) > 2"
- This is because if the inputs are all greater than 0, the outputs will all be greater than 2
- This could be seen from a sketch or by substituting inputs of x > 0 into f(x)
- f(x) = x2 with domain "all values of x"
- The range is f(x) ≥ 0
- This is because all values of x get squared (so no negative outputs are created)
- f(x) = 3x + 2 with domain x > 0
How do I solve problems involving the domain and range?
- You need to be able to identify and explain any exclusions in the domain of a function
- You need to be able to deduce the range of a function from its expression and domain

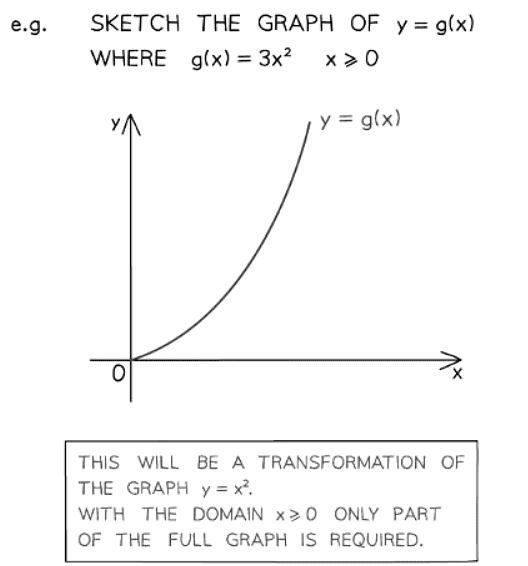
- You may also be asked to sketch a graph of a function
- This could involve sketching parts of familiar graphs that are restricted because of the domain and exclusions
The document Functions Toolkit | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on Functions Toolkit - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the main purpose of the Functions Toolkit in CIE IGCSE Maths: Extended? |  |
Ans. The main purpose of the Functions Toolkit in CIE IGCSE Maths: Extended is to help students understand the notation, principles, and relationships involved in functions.
| 2. How are input and output relationships represented in functions? |  |
Ans. Input and output relationships in functions are represented by mapping diagrams, which visually show how each input corresponds to a specific output.
| 3. How can students expand brackets and simplify functions in the Functions Toolkit? |  |
Ans. Students can expand brackets and simplify functions by applying the rules of algebra to combine like terms and simplify expressions.
| 4. What is the significance of understanding how functions work in the context of CIE IGCSE Maths: Extended? |  |
Ans. Understanding how functions work is essential in CIE IGCSE Maths: Extended as it forms the foundation for solving more complex mathematical problems involving functions.
| 5. How can students define a second function within the Functions Toolkit? |  |
Ans. Students can define a second function within the Functions Toolkit by following the same principles and notation used to define the first function, ensuring clarity and accuracy in the representation of both functions.
Related Searches





















