Fundamental Formulae for Differentiation | Physics for JEE Main & Advanced PDF Download
What is Differentiation?
- Differentiation is a fundamental concept in physics that helps us understand how quantities change with respect to one another. In simple terms, it's like finding the rate at which something is changing. For example, in physics, we might want to know how the velocity of an object changes over time, or how the temperature of a substance changes with respect to its volume.
- In essence, differentiation allows us to analyze and predict the behavior of physical systems by examining how variables such as position, velocity, acceleration, temperature, or pressure change over time or space.
- The rate of change of one quantity with respect to another quantity has great importance. For example, the rate of change of displacement of a particle with respect to time is called its velocity, and the rate of change of velocity is called its acceleration. The rate of change of a quantity ‘y’ with respect to another quantity ‘x’ is called the derivative or differential coefficient of y with respect to x.
 Representation of Rate of Change
Representation of Rate of Change
Differentiation of algebraic functions
- Differentiation of algebraic functions involves finding the rate at which a function changes with respect to its independent variable. It's like calculating the slope of a curve at a specific point.
- Using rules like the power rule, product rule, and chain rule, we can find the derivative of algebraic functions such as polynomials, rational functions, and exponential functions.
- This process helps us understand how functions behave locally and globally, and it's essential in fields like physics, engineering, and economics for analyzing rates of change and optimizing functions.
- Some common formulas for differentiation of algebraic functions are listed below:



Differentiation of trigonometric functions
- Differentiation of trigonometric functions involves finding the rate of change of trigonometric expressions with respect to a variable, typically denoted as x.
- We use rules such as the chain rule and product rule to differentiate trigonometric functions, enabling us to solve problems related to motion, oscillation, and many other real-world scenarios.
- Differentiation of Trigonometric Ratios are listed below:






Differentiation of logarithmic and exponential functions
- Differentiation of Logarithmic and Exponential Functions are listed below:

Differentiation of inverse trigonometrical functions
- Inverse trigonometric functions are operations that reverse the effects of trigonometric functions. While trigonometric functions take an angle as input and output a ratio of sides in a right triangle, inverse trigonometric functions take a ratio of sides as input and output the angle associated with that ratio.
- For example, if you have the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle, the arcsine function (sin⁻¹) will give you the angle whose sine is that ratio. These functions are essential for solving trigonometric equations and finding angles in various mathematical and real-world contexts.
- Differentiation of Inverse Trigonometric Functions are listed below:


 for |x| > 1
for |x| > 1

Differentiation of hyperbolic functions
- Hyperbolic functions are analogs of trigonometric functions but for hyperbolas instead of circles. They include hyperbolic sine (sinh), hyperbolic cosine (cosh), hyperbolic tangent (tanh), and others.
- These functions are defined in terms of exponentials and help solve problems related to hyperbolic geometry, physics, and engineering.
- Differentiation formulas for Hyperbolic functions are listed below:
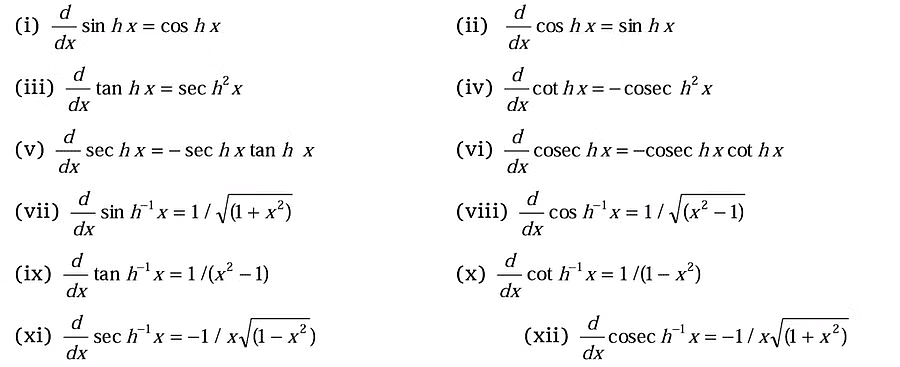 Differentiation of Hyperbolic Functions
Differentiation of Hyperbolic Functions
Differentiation by inverse trigonometrical substitution
- Differentiation by inverse trigonometric substitution involves using the inverse trigonometric functions to simplify complicated integrals.
- By substituting expressions involving these inverse functions, we can transform complex equations into simpler forms that are easier to solve using standard differentiation techniques.
 Differentiation by Inverse Trigonometrical Substitution
Differentiation by Inverse Trigonometrical Substitution
Some suitable substitutions
- Following substitutions can be used to simplify complex expressions:
 Some Important Substitutions
Some Important Substitutions
Product and Division Rule
While we perform differentiation of 2 functions either in multiplication and /or divisiom we will use the rules mentioned below
- Derivative of product of 2 functions is given by the product rule. Let ‘u’ and ‘v’ be 2 functions then
(uv)’ = u’v+ uv’
d(f(x).g(x))= d(f(x))/dx.g(x) + f(x).d(g(x))/dx - Derivative of quotient of 2 functions is given by the quotient rule (if the denominator is non zero)
(u/v)’ = ( u’v-uv’)/v2
d(f(x)/g(x))= (d(f(x))/dx .g(x) – d(g(x))/dx .f(x))/(g(x))2
Chain Rule
The Chain Rule, also called the outside-inside rule or composite function rule, is used to find derivatives of composite functions.
Steps for Chain Rule:
1. Identify the Chain Rule: The function should be composite.
2. Identify the inner and outer functions.
3. Find the derivative of the outer function while leaving the inner function.
4. Find the derivative of the inner function.
5. Multiply the results from step 3 and step 4.
6. Simplify the chain rule derivative.

Solved Examples on Differentiation
Question 1: Find the derivative of the function x2cos x.
Solution:
Given function is x2cos x
Let y = x2cos x
Differentiate with respect to x on both sides.
Then, we get:
dy/dx = (d/dx)x2cos x
Now, using the formula, we can write the above form as:
dy/dx = x2 (d/dx) cos x + cos x (d/dx)x2
Now, differentiate the function:
dy/dx = x2 (-sin x) + cos x (2x)
Now, rearrange the terms, we will get:
dy/dx = 2x cos x – x2 sin x
Question 2: Determine the derivative of cosx/(1+sin x).
Solution:
Given function: cosx/(1+sin x)
Let y = cosx/(1+sin x)
Now, differentiate the function with respect to “x”, we get
dy/dx = (d/dx) (cos x/(1+sin x))
Now, use the u/v formula in the above form, we get
dy/dx = [(1+sin x)(-sin x) – (cos x)(cos x)]/(1+sin x)2
dy/dx = (-sin x – sin2x-cos2x)/(1+sin x)2
Now, take (-) outside from the numerator, we get:
dy/dx = -(sin x + sin2.x + cos2x)/(1+sin x)2
We know that sin2.x + cos2x = 1
By substituting this, we can get:
dy/dx = -(1+sin x)/(1+sin x)2
Cancel out (1+sin x) from both numerator and denominator, we get:
dy/dx = -1/(1+sin x)
Therefore, the derivative of cosx/(1+sin x) is -1/(1+sin x).
Question 3: Evaluate the derivative of f(x) = sin2x using Leibnitz product rule.
Solution:
Given function: f(x) = sin2x
Let y= sin2x
Now, by using Leibnitz product rule, we can write it as:
dy/dx = (d/dx) sin2x
Sin2x can be written as (sin x)(sin x)
Now, it becomes:
dy/dx = (d/dx) (sin x)(sin x)
dy/dx = (sin x)’(sin x) + (sin x)(sin x)’
dy/dx = cos x sin x + sin x cos x
dy/dx = 2 sin x cos x
dy/dx = sin 2x
Therefore, the derivative of the function sin2x is sin 2x.
|
289 videos|635 docs|179 tests
|
FAQs on Fundamental Formulae for Differentiation - Physics for JEE Main & Advanced
| 1. How do you differentiate algebraic functions? |  |
| 2. What is the process for differentiating trigonometric functions? |  |
| 3. How do you differentiate logarithmic and exponential functions? |  |
| 4. What are some common hyperbolic functions that can be differentiated? |  |
| 5. How do you use inverse trigonometrical substitution for differentiation? |  |

|
Explore Courses for JEE exam
|

|


















