Galilean and Lorentz Transformations | Modern Physics PDF Download
Galilean Transformations
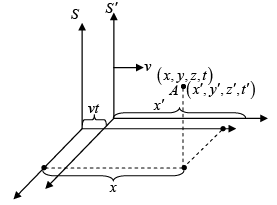
Suppose frame S' is moving with constant velocity v relative to an inertial frame S. The transformation equations between the two frames is 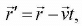 , x' = x - vt, y' = y, z' = z, t' = t
, x' = x - vt, y' = y, z' = z, t' = t
The above transformations of coordinates from one inertial frame to another are referred to as Galilean transformations.
And inverse Galilean transformation is given by
x = x' + vt, y = y', z = z', t = t'
The velocity transformation is given
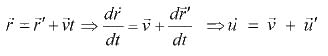
Tire acceleration transformation is given
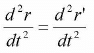
It is found that the acceleration measured in both frames is the same. So it is an inertial frame.
When velocity transformation is analyzed as u' = c, where c is the velocity of light.
u = c + v
It is seen that the velocity of light is dependent on the reference frame which is physically not accepted. So, for high velocity i.e., v ≈ c, Galilean transformation is inadequate.
So, for velocity u ≈ c, there is a need for different types of transformation, which is given by Lorentz transformation.
Lorentz Transformation
Postulates of Special Theory of Relativity
(i) There is no universal frame of reference pervading all over space, so there is no such thing as "absolute motion”.
(ii) The law of Physics is the same in all frames of reference moving at constant velocity with respect to each other.
(iii) The speed of light in free space has the same value for all inertial observers.
Derivation of Lorentz Transformation
Lorentz transformation has to be such that
(a) It is linear in x and x', so that a single event in frame S corresponds to a single event in frame S'.
(b) For lower velocity it reduces to Galilean transformation.
(c) The inverse transformation exists.
Let us assume
x' = k (x - vt), x = k (x' + vt') ,y' = y and z' = z
Putting the value, x' = k (x - vt) in x = k (x' + vt') one will get,
x= k2 (x - vt) + kvt' and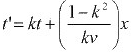
Now, x = ct in S frame and x' = ct' in S' frame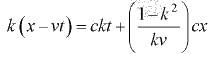
Solving this equation for k, then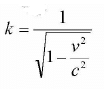

Consequences of Lorentz Transformation
Length Contraction
To measure the length of an object in motion, relative to the observer, the position of two endpoints is recorded simultaneously. The length of the object in the direction of motion appeared smaller to the observer.
I0 = x'2 - x'1, I = x2 - x1
x'2 - x'1 = γ(x1 - vt) - γ(x2 - vt)
(x'2 - x'1) = γ(x2 - x1)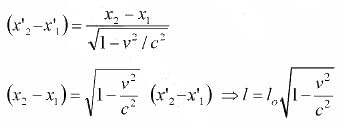
Thus l < l0, this means that the length of the rod as measured by an observer relative to which the rod is in motion, is smaller than its proper length.
Such a contraction of length in the direction of motion relative to the observer is called Lorentz Fitzgerald contraction.
Time Dilation
When two observers are in relative uniform motion and uninfluenced by any gravitational mass, the point of view of each will be that the other's (moving) clock is ticking at a slower rate than the local clock. The faster the relative velocity, the greater the magnitude of time dilation. This case is sometimes called a special relativistic time dilation.
A clock being at rest in the S' frame measures the time t'1 and t'2 of two events occurring at a fixed position x'. The time interval Δt measures from S frame appears slow (Δt0) from S' frame i.e., to the observer, the moving clock will appear to go slow.
Δt' = t'2 - t'1 = Δt0 ⇒ Δt = t2 - t1
Δt0 → Proper time, Δt → time interval measured from S frame Δt > Δt0
|
37 videos|17 docs|19 tests
|
FAQs on Galilean and Lorentz Transformations - Modern Physics
| 1. What are Galilean Transformations and how do they differ from Lorentz Transformations? |  |
| 2. What are the consequences of Lorentz Transformations in terms of relativistic effects? |  |
| 3. How does the concept of relativistic energy differ from classical energy in the context of special relativity? |  |
| 4. How is the Doppler Effect in light different from the Doppler Effect in sound, and how is it related to the concept of relative velocity? |  |
| 5. What role do four vectors play in maintaining relativistic invariance in physical equations, and how do they differ from three-dimensional vectors in classical mechanics? |  |





















