Games and Tournaments: Solved Examples | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
In this post, we will talk about all the concepts we will require while solving questions identified with games and tournaments. This subject can now and again involve some essential understanding of the games mentioned in the riddle. One should realize some common terminologies utilized by the examiners in the questions.
Round Robin
Round Robin is a tournament where each team plays with every other team. Suppose there are 8 teams in a tournament then every teams will play seven matches. This is known as single round robin. When every team plays with every other team exactly once, then it is called single round robin. We all know about IPL, right. In IPL, every team plays with every other team twice. This is double round robin, where each team plays every other team two times. That means, for a tournament of eight teams, each team gets to play 14 matches. The winner (or the rankings) is decided based on all the matches. A few things to remember regarding the matches:
- Total number of matches for a single round robin is NC2, where N is the total number of teams participating in the tournament.
- If there is no draws, the number of wins is equal to the number of matches. It applies for number of losses as well.
- In case there are draws, total number of wins + (total draws/2) = total number of matches.
There are two key points for this type of question:
1. If we are finding maximum number or points for a team then start distribution of the point from bottom to top.
2. If we are finding minimum number or points for a team then start distribution of the point from top to bottom.
We will see above cases in following example.
Example: There are 16 teams and they are divided into 2 groups of 8 each. Each team in a group plays against one another on a round-robin basis. Two points are awarded for a win, one point for a tie and zero for a loss. The top four teams from each group will qualify for the next round i.e. round 2. In Round 2, each team of one group will play with each team of group two. At the end of the second round, the top four teams in terms of the points scored advance to the semi finals and the winners of the semi finals play the finals. In case of teams having the same number of wins, the team with better run-rate would be ranked ahead.
(Note: Write down all the key points which are mentioned in the questions.
Like,
Total 16 teams
Two group - Each group having 8 teams.
Points - Win: 2, Tie / Draw: 1, Loss: 0
Top four from each group will go to the next round.(4 Matches)
Semi Finals (2 Matches), Final.)
Questions can be asked in this type of tournament based scenario:
i) What is the total number of matches played in the tournament?
a) 50
b) 56
c) 28
d) 75
Ans: d) 75
Total matches = Number of group A matches + Number of group B matches + Round 2 + Semi-Finals + Final
= 82 + 8C2 + 4C1 x 4C1 + 2 + 1
= 28 + 28 + 16 + 2 + 1 = 75 matches
ii) What is the least number of points with which a team can advance to the round 2?
a) 5
b) 4
c) 10
d) 8
Ans: a) 5
As we have seen in key points that if we are looking for minimum points then we will have to go from Top to Bottom.
In given question we have to find out "Least number of points" that means minimum number of points. SO we will have to start point distribution from Top to Bottom.
Now, let assume that top #1 team won all its 7 matches. (14 Points)
Top #2 team won all its matches except against #1 team. (12 Points)
Top #3 team won all its matches except against #1 and #2 matches. (10 Points)
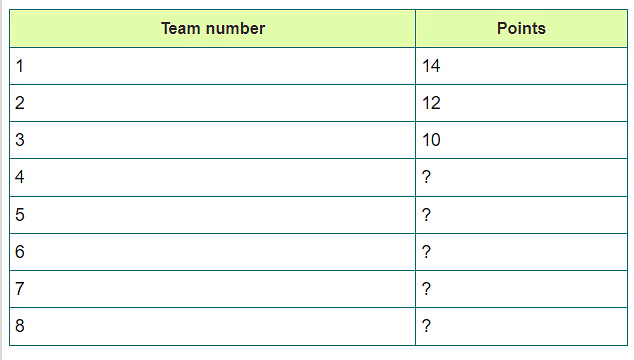
Now we are left with 20 points (i.e. Total points for group one matches 56 - (14 + 12 + 10) = 20).
Now remaining 5 teams have lost 3 matches with top teams. So, they are left with 4 matches with others. We will distribute remaining points equally to them i.e. 20 / 5 = 4.
So, remaining 5 teams will now have 4 - 4 points and here run rate checking scenario occurs.
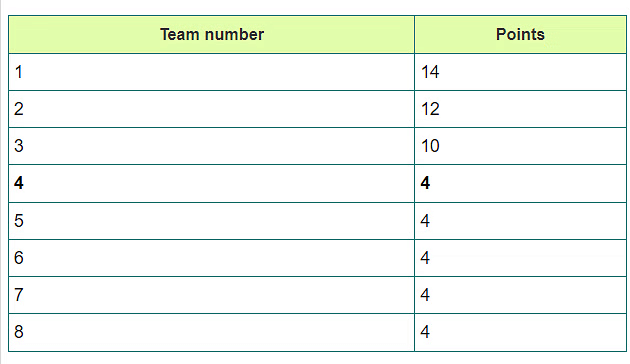 So, minimum or least 4 Points are required for getting into second round.
So, minimum or least 4 Points are required for getting into second round.
iii) What is the maximum possible number of points that can be scored by a team that is eliminated at the firstround?
a) 14
b) 12
c) 10
d) 8
Ans: c) 10
In this case we have to find out maximum possible number of points that can be scored by a team which is eliminated after first round (Simply, by Low run rate)
As we have mentioned in key points that for finding maximum points we have to start from bottom to top.
We will make a group of Bottom 3 teams and another of Top 5 teams.
Let’s assume that bottom 3 team will lose their matches against top teams. So, they will have total 3 matches left for winning. (Those 3 teams will play against each other) Total 6 points they can have. We will distribute those points equally between them. i.e. 2 points for each team.
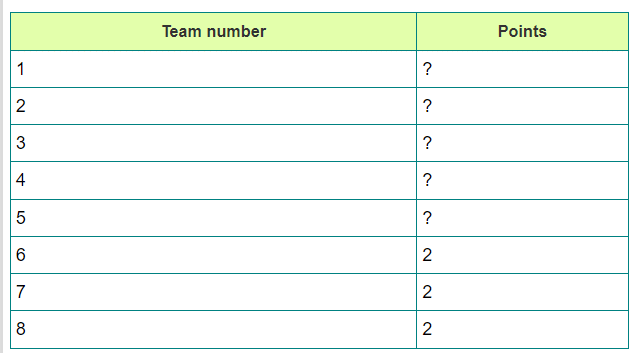
Now, we have to give top 5 teams equal points. So that we can have top 4 team in next round and team #5 is eliminated after first round though it can have maximum number of points.
So, remaining 50 points (i.e. Total points 56 - 6 Points distributed amongst bottom 3 teams = 50 Points) will be distributed equally amongst 5 team that is 10.
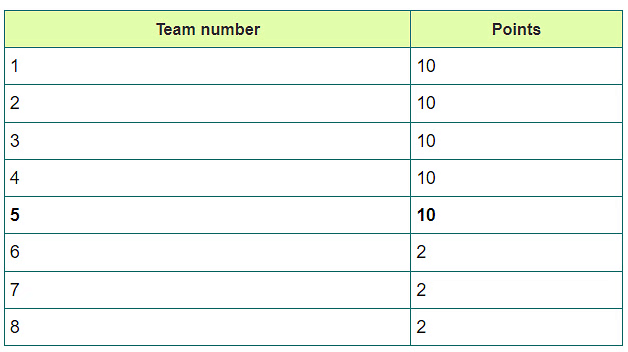
Now, team #5 will also have 10 Points but it will be out of the league because of low run rate. So, answer is 10.
iv) What is the minimum number of matches won by a team that reaches the finals?
a) 1
b) 2
c) 3
d) 4
Ans: a) 1
This is very simple because we can assume that all the matches of every round before semi-finals are drawn, and team enters in semi-finals with high net run rate.
So, to reach in final, Team has to win only one match. i.e. Semi-Final.
(This is only possible when in the question "Draw/Tie" scenario is given.)
So, answer is 1.
v) What is the maximum number of matches won by a team that reaches the finals?
a) 10
b) 16
c) 15
d) 12
Ans: d) 12
To find out maximum number of matches won by a team is very easy, because for maximum win a team has to win all the matches that it has played.
So, in this scenario team will play total 12 matches before final.
In first round, 7 Matches (Match with each team in the group.)
In second round, 4 matches (Match with each team of another group which enters in second round.)
In Semi-Final, one match.
So, Total 7 + 4 + 1 = 12 Matches, a team has to win to reach in finals.
Minimum Wins to Qualify
Similar to IPL (single round robin), if 4 teams qualify for the play-offs or the qualifier matches for the final, what should be the minimum number of matches a team needs to win in order to qualify.
For a tournament of 8 teams (say Team A, B, C, D, E, F, G, H), total number of matches is 8C2, that is 28 matches. If the question asks minimum number of wins (say M1), you need to consider no draw case (unless mentioned). Also, minimum number of wins DOES NOT MEAN that a team winning M1 matches will always qualify for the play-offs. It simply means that there is one particular case when a team winning only M1 matches (M1 can be unexpectedly small) can qualify for the play-offs. For 28 wins and 4 teams to qualify, we will maximize wins for the top 3 teams.
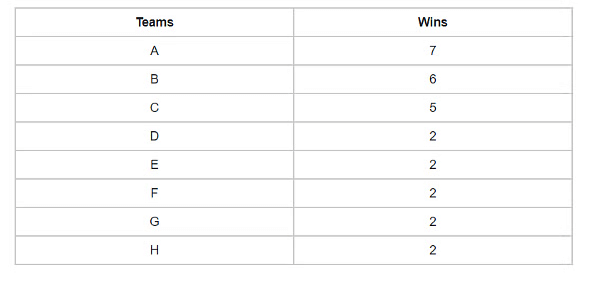
To maximize the number of wins for the top three teams, the top team (A) wins all the matches, i.e. 7, then the next team (B) will win 6 matches (the only match the second team lost is to the top team) and the third team (C) will win 5 matches. Summing up the wins for top 3 teams, it comes out to be 18 with only 10 wins remaining for the rest of the 5 teams. So, we distribute each team with 2 wins. The team D will qualify with the help of net run rate or some other parameter. In case of a football tournament, the parameter can be the number of goals. Similarly, this parameter will vary with different games. The answer for M1 is 2 in this case.
Maximum Number of Wins even after which a Team can go out of the Tournament
Like the previous case, we will consider no match drawn case. The team that will not qualify will be the fifth team (E). All the top 5 teams will have equal wins but the fifth team will lose out on the net run rate (or some other parameter mentioned). Top three teams win against the bottom three teams. Total 15 wins out of 28 are distributed. We are remaining with 13 wins to distribute. Now, each of top 5 teams have matches with each other as well, four matches for each team. Total matches among top 5 teams is5C2, i.e. 10. 10 matches, 10 wins, we distribute all the teams with 2 wins each. Hence, all the top 5 teams win 5 matches each but due to net run rate the fifth team will lose a place in the qualifiers.Another approach can be to distribute minimum wins from the bottom. Let us say H is the last team and it lost all the matches. It has 0 wins. G will win only one match against H and lose other matches. I will win 2 matches against G and H and lose other matches. Out of 28 wins, 3 wins distributed and 25 remaining. We can distribute 25 wins equally among the top 5 teams. In case the division in not equal, distribute extra wins to the top team, then to the second team and so on.Minimum wins to ensure a Place in Play-Offs
From the previous case, we can say even at 5 wins a team can lose a place in the play-offs. In order to qualify, a team must win at least 6 matches (with regards to the case we are discussing) to ensure a place in the play-offs. This case is different from the first case as in the first case, it is just one possibility whereas third case is always valid, it provide a guaranteed place in the playoffs.
 |
Download the notes
Games and Tournaments: Solved Examples
|
Download as PDF |
Knockout Tournaments
Knockout tournament is another very commonly asked structure in CAT. Every game is a knockout, which means the winner must have won all the matches. A knockout tournament has typically a number of rounds and in each round, a certain number of players are knocked out of the tournament.
Tennis is one particular game, which is frequently asked in CAT where knockout tournament is concerned.
The total number of players are generally 2k, where k is a natural number. There are cases when the number of players is not 2k. We will discuss them later. First, we will discuss the cases where we have 2k players. Few things to remember regarding such tournaments:
- Total number of matches = Total number of players – 1.
- Knockout tournaments will generally have seeded (ranked) players.
- Knockout tournaments will not have a tie. There will always be a tiebreaker. It is knockout after all.
- Upset means a lower seeded player defeat upper seeded player.
- The total number of rounds is k (from 2k) and kth round is the final round.
- First seeded player (rank 1) will play with last seeded player, rank 2 with second last seeded and so on.
Question: Let us take a case of 64 players. We know 26 is 64; therefore, there are 6 rounds. If player seeded 2 reached semi-final, then who could be his likely opponent.
Ans: Approach: First, we should know the number of possibilities. Semi-final is the fifth round that means any player in fifth round has won four matches.
Let us say ith seeded player is second seeded player’s opponent. Every time we will expand the value for i by subtracting 2 (initially for rank 2) from total players in round + 1. Let us form a chart to make the things easier. The chart shows the player second seeded player might have defeated(or played against) in different rounds.
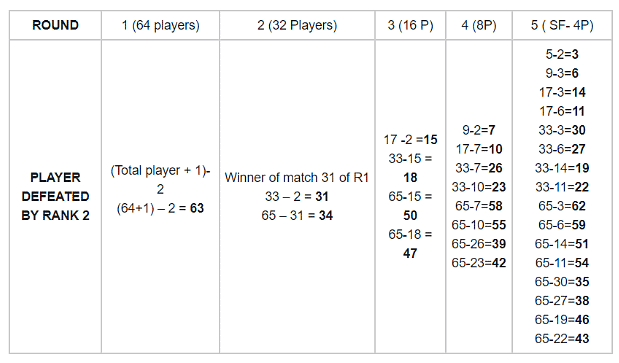 The bold number in the tables indicate the possibilities of opponents for the second seeded player in that particular round.
The bold number in the tables indicate the possibilities of opponents for the second seeded player in that particular round.
Semi-final has 16 possibilities or 2(round number -1) possibilities. The method is simple as we can see from the table. We subtract the rank from total number of players in that round +1. Next, the value obtained is minus from total players + 1 in previous round (say in R3, the previous round is R2).
- All the rank values obtained after this step is subtracted from the total players + 1 of the round before R2 (i.e. R1) and so on.
In case of no upsets, we will always take the lowest rank from the set of values, or just subtract from total players + 1 for that particular round. - In case of upset, you should try to find out the rank of the player, the higher seeded player would have played against.
If the number of player is not 2k, where k is a natural number, then there will be walkovers. - Remember, at the end we need a final match and it will require just two players. So, at some point in the tournament we will encounter an odd number which will make it difficult to have matches for all the players.
- Suppose, at some point there are 25 players, then we can have only 12 matches and player will get a walkover to next round or he/she might be knocked out at random.
- In any case, we can only have even number of players at every round. In such cases to find out the number of rounds (say k rounds), 2k-1< N < 2k, where N is the number of players at the start of the tournament.
- For example, if we have 70 players, then the number of rounds will be 7 as 26 < 70 < 27. The condition for walkover or bye could be either random or based on rank of the player; it will be mentioned in the question.
Let us understand this with the help of an example:
Example: 75 players participated in a tennis tournament, where every match is a knockout. If there are odd number of players in any round, then the top seeded player in that round gets a walkover to next round.
(i) If there are no walkovers from round 2 onwards, then how many matches are played in round 1.
(ii) If top seeded players of quarterfinal and semi-final are defeated in the upsets, what is the sum of the ranks of the players reaching the finals? Assume only one walkover per round.
Ans:
- Since round 2 onwards there are no walkovers, we need to make number of players 2k in round 2 itself. The 2k nearest to 75 and smaller than 75 is 64. Hence, we need to have 64 players in round 2.
- 75-64 = 11 players are knocked out in round 1, which means 11 matches have been played in round 1. This also means that 75-22 (11 matches between 22 players) = 53 players were granted a walkover to round 2.
- Since, the only two upsets mentioned are in quarterfinal and semi-final, top seeded player (rank 1) must have reached quarterfinal. Top seeded player is defeated in quarterfinal. Only 1 walkover allowed in every round to the top seeded player of that round, that top seeded player will always be rank 1 till quarterfinal. We need to know the number of player in every round.
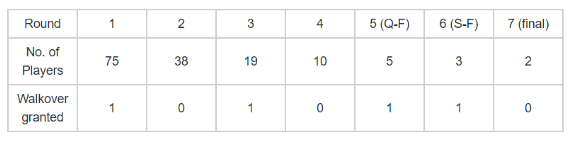
- We see that in quarterfinal, a walkover is granted. Since rank 1 is top-most seeded and is the one eligible for a walkover, the next top seeded player will definitely be rank 2. Rank 2 is defeated in Q-F. Again, in semifinal a player is granted a walkover, which will again be rank 1.
- Hence, rank 1 reached the final. Rank 2 is defeated in Q-F and since no other upsets in previous rounds are mentioned, rank 2 must have played against rank 5 in Q-F and rank 3 against rank 4 (rank 4 defeated rank 3 as top seeded players lose in QF and SF). In semifinal, rank 5 defeated rank 3. Final match is rank 1 vs rank 5. Sum of the ranks is 6.
- We see that the question asked is tricky and can be confusing at times. One needs to be clear with the terms used and have a understanding of the structure in the question. Otherwise, you might spend unnecessary time figuring out the structure itself.
- We talked about the two structures. Now, we will quickly discuss the win-loss table. The table is based mostly on either of the two structures, sometimes with little more information. Consider the following table:
- The following table shows the points scored by the teams in a cricket tournament. A win is rewarded with 2 points. In case of a tie, each team gets 1 point. Each team plays with every other team exactly once in the tournament. Only two teams have same points.Two pairs have same number of wins and one pair has same number of losses. Some of the entries in the table are missing:
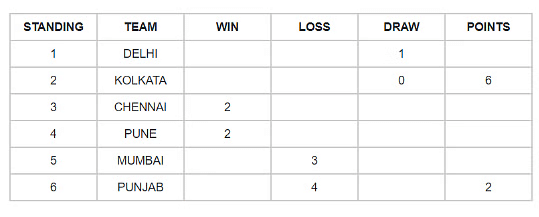
This table looks difficult to fill and involves a lot of iterations.We know the following things:
- 6 teams, total matches are 6C2 = 15.
- Total wins + (total draw/2) = 15
- Each team played 5 matches
From the table, we see that Punjab has 2 points. 2 points are possible either by 1 win or by 2 ties and Punjab had already lost 4 matches, therefore, only possibility is a win. Punjab 1 W, 4 L, 0 D. Kolkata has 6 points with 0 draw. Hence, 3 W for Kolkata and remaining 2 matches were lost. We know that two teams have same score. The three possibilities are Kolkata and Chennai or Chennai and Pune or Pune and Mumbai. WHY? Delhi has one draw and hence will have odd points. Mumbai and Punjab is not possible.
Let us start with lower one. If Pune and Mumbai have same points, Mumbai should have 2 wins and 4 points. Pune will be 2 W, 3 L, 0 D, 4 points. Chennai would therefore be with 5 points. As Chennai already has 2 W, for 5 points it needs a draw. So Chennai is finally 2 W, 2 L, 1 D, 5 points. Total wins till now = 3 (Kolkata) + 2 (Chennai) + 2 (Pune) + 2(Mumbai) + 1(Punjab) = 10. We have 1 draw match and 4 wins remaining. All 4 are won by Delhi. We missed out the condition that two pairs have same number of wins. Hence, our assumption that Pune and Mumbai have same points is wrong.
If Chennai and Pune have same points then, Chennai – 2 W, 3 L, 0 D; Pune – 2 W, 3 L, 0 D; Mumbai – 1 W, 3 L, 1 D; Delhi will have 5 wins and 1 draw, which is impossible. Another possibility is, , Chennai – 2 W, 2 L, 1 D; Pune – 2 W, 2 L, 1 D; Mumbai – 1 W, 3 L, 1 D. Here, we have three teams with same number of losses (Kolkata, Chennai, and Pune) but as per the question only one pair (two teams) has same number of losses.
Finally, we try to balance Kolkata and Chennai for same points. We get, Kolkata – 3 W, 2 L, 0 D; Chennai – 2 W, 1 L, 2 D; Pune – 2 W, 3 L, 0 D; Mumbai – 1 W, 3 L, 1 D; Delhi 4 W, 0 L, 1 D. We got two teams with same points, two pairs with same number of wins and one pair with same number of losses. The procedure involved much iteration which makes it time consuming.
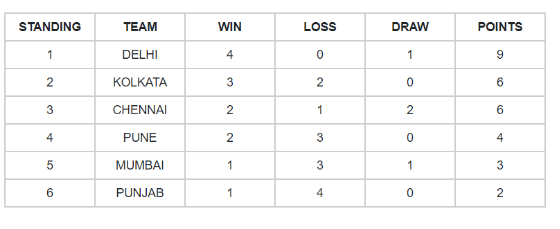
Win- loss table is sometimes time consuming and should be practiced thoroughly. Games like race events can be solved with linear arrangement concepts. Try solving more and more tables to get acquainted with the basic details used in the table.
Example: In the table below is the listing of Teams, seeded from highest (#1) to lowest (#16), who are due to play in an Association of Cricket tournament. This tournament has three knockout rounds before the final, i.e., first round, Quarter-finals, and semi-finals. In the first round, the highest seeded team plays the lowest seeded team (seed#16) which is designated match No. 1 of first round; the 2nd seeded team plays with the 15th seeded team which is designated match No. 2 of the first round, and so on. Thus, for instance, match No. 8 of first round is to be played between 8th seeded team and the 9th seeded team. In the second round, the winner of match No. 1 of first round plays the winner of match No. 8 of first round and is designated match No. 1 of second round. Similarly, the winner of match No. 2 of first round plays the winner of match No. 7 of first round, and is designated match No. 2 of second round. Thus, for instance, match No. 4 of the second round is to be played between the winner of match No. 4 of first round and the winner of match No. 5 of first round. The same pattern is followed for later rounds as well.
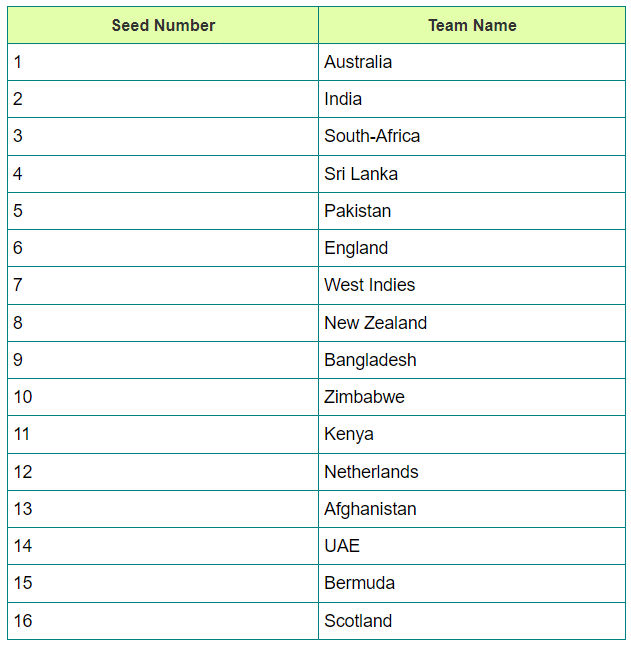 i) If there are no upsets in the first round, and only match Nos. 2, 3, and 4 of the second round result in upsets, then who would meet Pakistan in semi finals, in case Pakistan reaches semi finals?
i) If there are no upsets in the first round, and only match Nos. 2, 3, and 4 of the second round result in upsets, then who would meet Pakistan in semi finals, in case Pakistan reaches semi finals?
a) India
b) England
c) Australia
d) Didn’t reach in semi finals
Ans: c) Australia
In round 1 there were no upset, but in round two upsets in match No. 2, 3 and 4 (i.e. match between Seed No. 2 and 7, 3 and 6, 4 and 5 respectively).
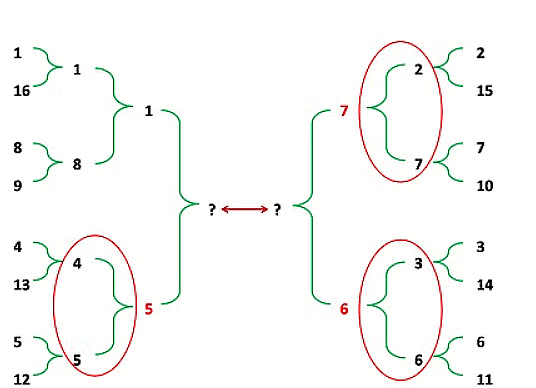 So, Pakistan (i.e. Seed no. 5) will face Australia (i.e. Seed no. 1) in semi finals.
So, Pakistan (i.e. Seed no. 5) will face Australia (i.e. Seed no. 1) in semi finals.
So, answer is Australia.
ii) If South-Africa and Sri-Lanka lose in the first round, while Bangladesh and India make it to the semifinals, then who would play with Australia in the second round, in the event Australia reaches second round?
a) Bangladesh
b) Scotland
c) New Zealand
d) India
Ans: a) Bangladesh
According to given terms, Seed No. 2 (India) and 9 (Bangladesh) reaches semi-finals. So, they must have won all the preceding rounds.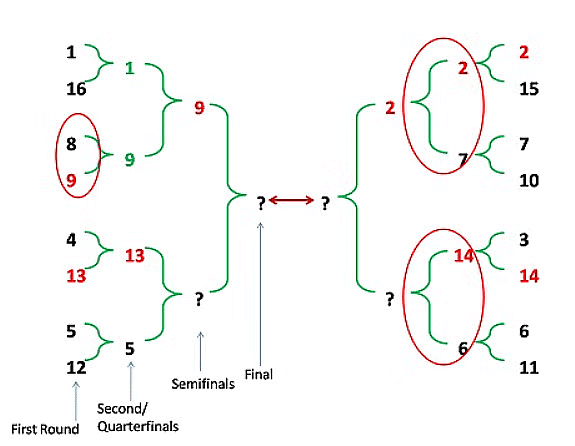 So, from above diagram we can see that Bangladesh played against Australia in second round.
So, from above diagram we can see that Bangladesh played against Australia in second round.
iii) If, in the first round, all even numbered matches (and none of the odd numbered ones) result in upsets, and there are no upsets in the second round, then which team facing South-Africa in semi-finals?
a) Australia
b) West-Indies
c) Bermuda
d) India
Answer: b) West-Indies
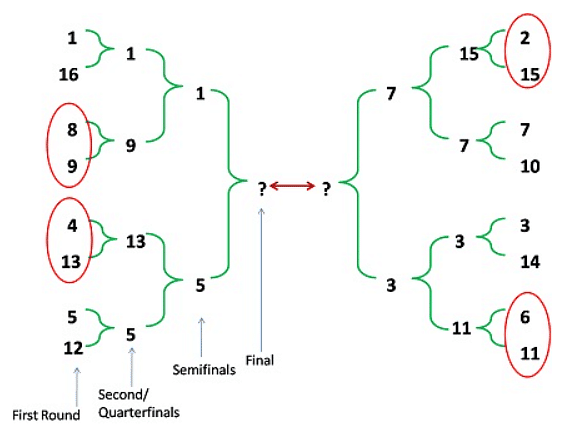
In the diagram, we can see that upsets are in even numbered matches i.e. matched between 2 and 15, 4 and 13, 6 and 11, 8 and 9 respectively.
And there are no upsets in second round.
So, from that in semi-finals South-Africa (Seed no. 3) faces West-Indies.
iv) How many matches are played in this tournament for getting final winner?
a) 32
b) 24
c) 16
d) 15
Ans: d) 15
In knockout tournament, total n - 1 matches are played for getting final winner. Here n=16, so total 16 - 1 = 15 matches are played.
Key Points
- If G, H and I is your answer and options are G and H, H and I, G and I and "None of the above" then you should mark "None of the above".
- M lost to N but won against O and P means M won against O and P.
- M lost to N who in turn won against O and P means N won against O and P.
- If it is given that "M did not win against N" then it does not necessarily mean that N won. In such a case draw/ tie is a possible conclusion.
- Standing are the positions (Like position in point table) of a team after completion of a round/ part of tournament.
- If you have taken more than 5 minutes to read and draw a possible table/ format and you are still not getting clean data then you must leave that question and move on to the next problem, because sometimes overlooking on a data point results into getting stuck in the sets. So take a break from that question and then approach these questions again afresh.
- Knock-out matches are those in which loser exits from the tournament.
- In a knock-out tournament, if n number of teams or n number of players is given then total n-1 number of matches is played. Also, in case of "Bye" system this logic is true.
For example, If there are 10 teams in a knock-out tournament then there should be 9 (i.e. 10 - 1 (n - 1)) matches played. - Round-Robin tournaments are those in which each team has to play fixed number of matches before eliminating or winning the tournament.
Each team has to play a match with each other teams exactly once then it is also a Round-Robin type of tournament. - In a Round-Robin tournament, we will have a total nC2 matches.
For example, if there are 10 teams in a round-robin tournament and given that each team has to play with each other team exactly once then total number of matches (for a particular round) are nC2= 10C2= 45.
|
92 videos|123 docs|94 tests
|
FAQs on Games and Tournaments: Solved Examples - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are some popular games often featured in tournaments? |  |
| 2. How can someone participate in a gaming tournament? |  |
| 3. What are the different formats of gaming tournaments? |  |
| 4. What are the benefits of participating in gaming tournaments? |  |
| 5. How can someone stay updated on upcoming gaming tournaments? |  |























