Gas Laws, Kinetic Energy & Gas Equations | Physics for JEE Main & Advanced PDF Download
Kinetic Theory:
Assumptions of Kinetic Theory of Gases:
- Every gas consists of extremely small particles known as molecules. The molecules of a given gas are all identical but are different from those of another gas.
- The molecules of a gas are identical spherical, rigid and perfectly elastic point masses.
- Their molecular size is negligible in comparison to intermolecular distance (10-9 m).
- The speed of gas molecules lies between zero and infinity (very high speed).
- The distance covered by the molecules between two successive collisions is known as free path and mean of all free path is known as mean free path.
- The number of collision per unit volume in a gas remains constant.
- No attractive or repulsive force acts between gas molecules.
- Gravitational to extremely attraction among the molecules is ineffective due small masses and very high speed of molecules.
Gas laws:
Assuming permanent gases to be ideal, through experiments, it was established that gases irrespective of their nature obey the following laws.
Boyle’s Law:
At constant temperature the volume (V) of given mass of a gas is inversely proportional to its pressure (p), i.e.,
V ∝ 1/p ⇒ pV = constant
For a given gas, p1V1 = p2V2
Fig: Boyle's law
Charles’ Law:
At constant pressure the volume (V) of a given mass of gas is directly proportional to its absolute temperature (T), i.e.,
V ∝ T ⇒ V / T = constant
For a given gas, V1/T1 = V2/T2
At constant pressure the volume (V) of a given mass of a gas increases or decreases by 1/273.15 of its volume at 0°C for each 1°C rise or fall in temperature.
Fig: Charles' law
Volume of the gas at t°Celsius:
Vt = V0 (1 + t/273.15)
where V0 is the volume of gas at 0°C.
Gay Lussacs’ or Regnault’s Law:
At constant volume, the pressure p of a given mass of gas is directly proportional to its absolute temperature T, i.e. ,
p ∝ T ⇒ V/T = constant
For a given gas,
p1/T1 = p2/T2
At constant volume (V) the pressure p of a given mass of a gas increases or decreases by 1/273.15 of its pressure at 0°C for each l°C rise or fall in temperature.
Fig: Gay Lussacs' law
Volume of the gas at t°C, pt = p0 (1 + t/273.15)
where P0 is the pressure of gas at 0°C.
Avogadro’s Law:
Avogadro stated that equal volume of all the gases under similar conditions of temperature and pressure contain equal number molecules. This statement is called Avogadro’s hypothesis. According to Avogadro’s law,
(i) Avogadro’s number: The number of molecules present in 1g mole of a gas is defined as Avogadro’s number.
NA = 6.023 X 1023 per gram mole
(ii) At STP or NTP (T = 273 K and p = 1 atm 22.4 L of each gas has 6.023 x 1023molecules.
(iii) One mole of any gas at STP occupies 22.4 L of volume.
Standard or Perfect Gas Equation:
Gases which obey all gas laws in all conditions of pressure and temperature are called perfect gases.
Equation of perfect gas pV=nRT
where p = pressure, V = volume, T = absolute temperature, R = universal gas constant and n = number of moles of a gas.
Universal gas constant R = 8.31 J mol-1K-1.
Real Gases:
Real gases deviate slightly from ideal gas laws because:
- Real gas molecules attract one another.
- Real gas molecules occupy a finite volume.
Real or Van der Waal’s Gas Equation:
(p + a/V2) (V – b) = RT
where a and b are called Van der Waal's constants.
Pressure due to an ideal gas is given by
p = (1/3).(mn/V). c2 = 1/3 ρ c2
For one mole of an ideal gas
P = (1/3).(M/V).c2
where, m = mass of one molecule, n = number of molecules, V = volume of gas, c = (c12+ c22 + … + cn2) / n all the root mean square (rms) velocity of the gas molecules and M = molecular weight of the gas. If p is the pressure of the gas and E is the kinetic energy per unit volume is E, then
p = (2/3).E
Kinetic Energy of a Gas:
(i) Average kinetic energy of translation per molecule of a gas is given by:
E = (3/2) kt
where k = Boltzmann’s constant.
(ii) Average kinetic energy of translation per mole of a gas is given by:
E = (3/2) Rt
where R = universal gas constant.
(iii) For a given gas kinetic energy
E ∝ T ⇒ E1/E2 = T1/T2
(iv) Root mean square (rms) velocity of the gas molecules is given by:
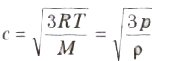
(v) For a given gas c ∝ √T
(vi) For different gases c ∝1/√M
(vii) Boltzmann’s constant k = R/N
where R is ideal gas constant and N = Avogadro number.
Value of Boltzmann’s constant is 1.38 x 10-28 J/K.
(viii) The average speed of molecules of a gas is given by
(ix) The most probable speed of molecules of a gas is given by
⇒
Important Points:
(i) With rise in temperature rms speed of gas molecules increases as
(ii) With the increase in molecular weight rms speed of gas molecule decrease as(iii) Rms speed of gas molecules is of the order of knn/s, eg., at NTP for
hydrogen gas(iv) Rms speed of gas molecules does not depend on the pressure of gas !if temperature remains constant) because p ∝ p (Boyle s law). If pressure is increased n times, then density will also increase by n times but vrms remains constant.
|
320 videos|994 docs|210 tests
|
FAQs on Gas Laws, Kinetic Energy & Gas Equations - Physics for JEE Main & Advanced
| 1. What are the gas laws? |  |
| 2. How does kinetic energy relate to gas molecules? |  |
| 3. What is the ideal gas law equation? |  |
| 4. How do gas laws apply to real gases? |  |
| 5. How can gas laws be applied in everyday life? |  |

















