Gauss' Law | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
GAUSS’ LAW
The mathematical relation between electric flux and the enclosed charge is known as Gauss law for the electric field. It is one of the fundamental laws of electromagnetism.
The law was proposed by Joseph- Louis Lagrange in 1773 and later followed and formulated by Carl Friedrich Gauss in 1813.
Let us consider a positive point charge q located at the centre of a sphere of radius r, as shown in figure
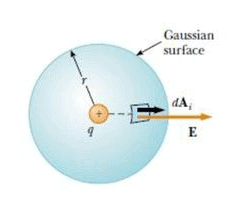
From the equation, E = we know that the magnitude of the electric field everywhere on the surface of the sphere is
we know that the magnitude of the electric field everywhere on the surface of the sphere is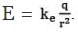
The field lines are directed radially outward and hence are perpendicular to the surface at every point on the surface . That is, at each surface point, E is parallel to the vector ΔAi representing a local element of area ΔAi surrounding the surface point. Therefore,
E ⋅ ΔAi = EΔAi
And from equation, Φ𝐸 = ∮𝐸 ⋅ 𝑑𝐴 = ∮ 𝐸𝑛 𝑑𝐴 we find that net flux through are gaussian surface is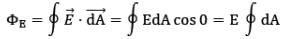
where we have moved E outside of the integral because, by symmetry, E is constant over the surface and given by E =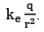 Furthermore, because the surface is spherical A=4πr2. Hence, the net flux through the gaussian surface is
Furthermore, because the surface is spherical A=4πr2. Hence, the net flux through the gaussian surface is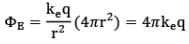
Now, we know that,
K𝑒 = 1/4𝜋ε₀
Therefore,
𝚽𝐄 = 𝐪/𝛆₀
Now, observe that the net electric flux through the spherical Gaussian surface depends only on the charge enclosed within the close Gaussian surface and the permittivity of the free space. It does not depend on the location of the charge or the Electric field produced by the charge.
Obviously, we derived it for the simplest charge configuration, but it holds true for all cases.
In general case,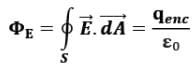
The electric flux (ΦE ) is independent of the radius r because the area of the spherical surface is proportional to r2 whereas the electric field is proportional to 1/r2. Thus, in the product of area and electric field, the dependence on r cancels.
Q. What if the charge in figure was not located at the centre of the spherical gaussian surface?
Ans. In this case, the situation does not possess enough symmetry to evaluate the electric field. Because the charge is not at the centre, the magnitude of 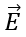 would vary over the surface of the sphere and the vector
would vary over the surface of the sphere and the vector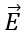 would not be everywhere perpendicular to the surface. But still the flux through the spherical surface is q/(ε₀).
would not be everywhere perpendicular to the surface. But still the flux through the spherical surface is q/(ε₀).
Note: the net flux through any closed surface surrounding a point charge q is given by q/(ε₀) and is independent of the shape of that surface.
GAUSS LAW FOR MULTIPLE CHARGES
Let us calculate flux for many charges. We once again use the superposition principle, which states that the electric field due to many charges is the vector sum of the electric fields produced by the individual charges. Therefore, we can express the flux through any closed surface as: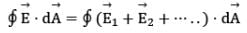 where
where 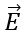 is the total electric field at any point on the surface produced by the vector addition of the electric fields at that point due to the individual charges. Consider the system of charges shown in figure.
is the total electric field at any point on the surface produced by the vector addition of the electric fields at that point due to the individual charges. Consider the system of charges shown in figure.
- The closed surface S surrounds only one charge q1, hence, the net flux through S is q1/ε₀.
- The flux through S due to charges q2, q3 and q4 outside it is zero because each electric field line that enters S at one point leaves it at another.
- The surface S’ surrounds charges q2 and q3; hence, the net flux through it is (q2+q3)/ε₀.
- Finally, the net flux through surface S” is zero because there is no charge inside this surface. That is, all the electric field lines that enter S” at one point leave at another.
- Notice that charge q4 does not contribute to the net flux through any of the surfaces because it is outside the entire surface.
Gauss’s law, which is a generalization of what we have just described, states that the net flux through any closed surface is
where qenc represents the net charge inside the surface and represents the electric field at any point on the surface.
represents the electric field at any point on the surface.
Some points to be emphasized about the gauss law
- It is true for any closed surface no matter what its shape and size.
- The q includes algebraic sum of all charges enclosed by the surface.
- In situations when the surface is so chosen that there are some charges inside and some outside, the
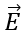 (whose flux appear in the equation) is due to all charges, just term 'q' in the law represents only total charge inside.
(whose flux appear in the equation) is due to all charges, just term 'q' in the law represents only total charge inside. - The gaussian surface should not pass through any discrete charge however; it can pass through a continuous charge distribution.
Note: That the gaussian surface should not contain any finite non-zero charge.
|
201 videos|410 docs|280 tests
|
FAQs on Gauss' Law - Physics for Airmen Group X - Airforce X Y / Indian Navy SSR
| 1. What is Gauss' Law? |  |
| 2. How is Gauss' Law applied to calculate electric fields? |  |
| 3. Can Gauss' Law be applied to non-symmetric charge distributions? |  |
| 4. How does Gauss' Law relate to Coulomb's Law? |  |
| 5. What are some real-life applications of Gauss' Law? |  |

















