General Aptitude- 2 | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Question 16: The CEO’s decision to quit was as shocking to Board as it was to __________.
(a) myself
(b) I
(c) me
(d) my
[2019 : 1 Mark, Set-I]
Answer: (c)
Solution: CEO’s decision to quit was as shocking to board as it was to me.
- Board and me are receives of the action hence objective case of pronoun (me) is to be used.
Question 17: The lecture was attended by quite _______ students, so the hall was not very_____.
(a) few, quite
(b) a few, quite
(c) few, quiet
(d) a few, quiet
[2019 : 1 Mark, Set-I]
Answer: (d)
Solution: The lecture was attended by quite a few students so the hall was not very quiet.
- quite a few indicates a fairly large number of units.
- quiet refer to making little or no noise.
Question 18: They have come a long way in ________ trust among the users.
(a) Creating
(b) Created
(c) Creation
(d) Create
[2019 : 1 Mark, Set-I]
Answer: (a)
Solution: They have came long way in creating trust among the users.
Question 19: On a horizontal ground, the base of a straight ladder is 6 m away from the base of a vertical pole. The ladder makes an angle of 45° to the horizontal. If the ladder is resting at a point located at one-fifth of the height of the pole from the bottom, the height of the pole is_______ meters.
(a) 15
(b) 25
(c) 35
(d) 30
[2019 : 1 Mark, Set-I]
Answer: (d)
Solution: Here tan 45° = 1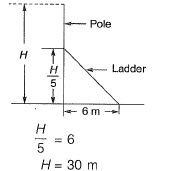
Height of wall = 30 m
Question 20: If E = 10; J = 20 ; O = 30 ; and T = 40, what will be P + E + S + T?
(a) 51
(b) 120
(c) 82
(d) 164
[2019 : 1 Mark, Set-I]
Answer: (b)
Solution: According to given coding
P = 32, E = 10, S = 38, T = 40
P + E + S + T = 32 + 10 + 38 + 40 = 120
Question 21: A faulty wall clock is known to gain 15 minutes every 24 hours. It is synchronized to the correct time at 9 AM on 11th July, What will be the correct time to the nearest minute when the clock shows 2 PM on 15th July of the same year?
(a) 12:45 PM
(b) 12:58 PM
(c) 1:00 PM
(d) 2:00 PM
[2018 : 2 Marks, Set-II]
Answer: (b)
Solution: 9 Am of 11 July of 2 PM on 15th July = 101 hours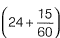 hours of incorrect clock = 24 hours of correct clock
hours of incorrect clock = 24 hours of correct clock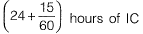
= 24 hours of correct clock
1 hour of IC = 96/97 hours of correct clock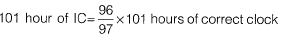
= 99.958 hours of correct clock
= 99 hours + 0.95876 x 60 minutes of correct clock
= 99 hours + 57.525 min.
= 99 hours and approx 58 min.
So, correct time will be
2 PM, 11th july + (99 hours and 58 minutes)
= 12: 58 PM on 15th July
Question 22: Given that 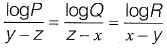 = 10 for x ≠ y ≠ z, what is the value of the product PQR?
= 10 for x ≠ y ≠ z, what is the value of the product PQR?
(a) 0
(b) 1
(c) xyz
(d) 10xyz
[2018 : 2 Marks, Set-II]
Answer: (b)
Solution: logP = 10(y - z)
logQ = 10(z - x)
logR = 10(x - y)
logP + logQ + logR = 0
log (PQR) = log 1
PQR = 1
Question 23: The annual average rainfall in a tropical city is 1000 mm. On a particular rainy day (24-hour period), the cumulative rainfall experienced by the city is shown in the graph. Over the 24-hour period. 50% of the rainfall falling on a rooftop, which had an obstruction-free area of 50 m2, was harvested into a tank. What is the total volume of water collected in the tank in liters?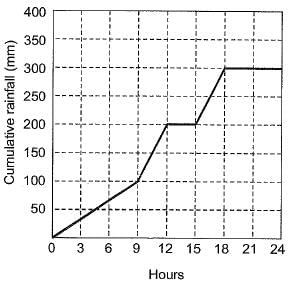
(a) 25,000
(b) 18,750
(c) 7,500
(d) 3,125
[2018 : 2 Marks, Set-II]
Answer (c)
Solution: Cumulative rainfall = 300 mm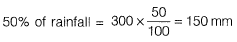
Area = 50 m2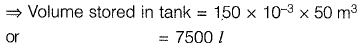
Question 24: Each of the letters in the figure below represents a unique integer from 1 to 9. The letters are positioned in the figure such that each of (A+B+C), (C+D+E), (E+F+G) and (G+H+K) is equal to 13. Which integer does E represent?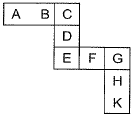
(a) 1
(b) 4
(c) 6
(d) 7
[2018 : 2 Marks, Set-II]
Answer: (b)
Solution:
A + B + C= 13 ,..(i)
C + D + E= 13 ...(ii)
E + F + G = 13 ...(iii)
G + H + K= 13 ...(iv)
Adding [(i) + (ii) + (iii) + (iv)]
A + B + C +D + E + F+ G + H + K+ (C + E + G) = 13 x 4 = 52 ...(v)
Also A, B, C, D, E, F, G, H& K represents natural numbers from (1 to 9)
There sum will be given by 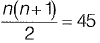
Substituting (iv) C + E + G - 7 ,..(vi)
Only possibly for sum 7 will be (1, 2, 4)
Now, C + E cannot be (1 and 2)
As eq. (ii) is C + D + E = 13
Now, D will become equal to 10 (which is not possible because digits 1 to 9 given)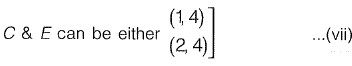
If C = H from eq. (vi) C + E + G = 7
Now, E + G = 3
(Not possible in eq. (iii) E + F + G = 10,
F - 10 which is not possible)
So from eq. (vii) only possibility remains is E = H.
Question 25: In manufacturing industries, loss is usually taken to be proportional to the square of the deviation from a target. If the loss is Rs. 4900 for a deviation of 7 units, what would be the loss in Rupees for a deviation of 4 units from the target?
(a) 400
(b) 1200
(c) 1600
(d) 2800
[2018 : 2 Marks, Set-H]
Answer: (c)
Solution: Loss = kd2
For duration of 7 units
4900 = k (7)2 ⇒ k = 100
Loss = kd2
For duration of 4 units
= k(4)2 ⇒ 16k = 1600
Question 26: What of the following function(s) in an accurate description of the graph for the range(s) indicated?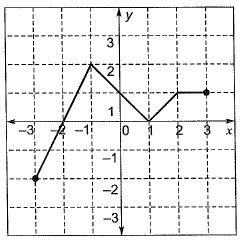
(a) y = 2x + 4 for -3 < x < ~ 1
(b) y = |x - 1| for -1 < x < 2
(c) y = | |x | - 1| for -1 < x < 2
(d) y = 1 for 2 < x < 3
(a) (i), (ii) and (iii) only
(b) (i), (ii) and (iv) only
(c) (i) and (iv) only
(d) (ii) and (iv) only
[2018 : 2 Marks, Set-I]
Anwser: (b)
Solution: Put value and verify
(i) y = 2x + 4 is true in -3 < x < - 1
On putting x = -3, y = -2 and x = -2,
y = 0 and x = -1, y = 2
(ii) y = |x - 1| is also true (x = -1, y = 2), (x = 0, y = 1) and (x = 1, y = 0)
(iv) y = 1 in (2 < x < 3) always true
(i), (ii) and (iv) are true.
Question 27: The price of a wire made of a superalloy material is proportional to the square of its length. The price of 10 m length of the wire is Rs. 1600. What would be the total price (in Rs.) of two wires of lengths 4 m and 6 m?
(a) 768
(b) 832
(c) 1440
(d) 1600
[2018 : 2 Marks, Set-I]
Answer: (b)
Solution: C ∝ W2
C = kW2
⇒ C= k(10)2 = 100k = 1600
⇒ k = 16
C1 = k(4)2 = 16k
C2 = k(6)2 = 36k
Now total cost = 52k = 52 x 16 = 832
Question 28: Each of the letters arranged as below represents a unique from 1 to 9. The letters are positioned in the figure such that (A x B x C), (B x G x E) and (D x E x F) are equal. Which integer among the following choices cannot be represented by the letters A, B, C, D, E, F or G?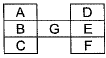
(a) 4
(b) 5
(c) 6
(d) 9
Answer: (b)
Solution: 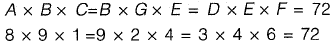
Any of A, B, C, D, E, F, G cannot be 5.
Question 29: A fruit seller sold a basket of fruits at 12.5% loss. Had he sold it for Rs. 108 more, he would have made a 10% gain. What is the loss in Rupees incurred by the fruit seller?
(a) 48
(b) 52
(c) 60
(d) 108
[2018 : 2 Marks, Set-I]
Answer: 12.5%x + 10%x = 108
x =108/22.5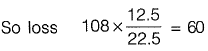
Question 30: Consider a sequence of number a1, a2, a3......, an where 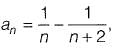 for each integer n > 0.
for each integer n > 0.
What is the sum of the first 50 terms?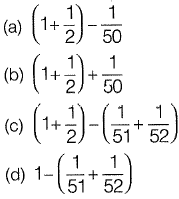
[2018 : 2 Marks, Set-I]
Answer: (c)
Solution: Sum of series will be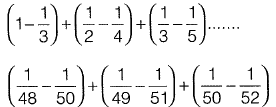
Ail like terms will cancel out and we will be left with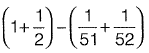
FAQs on General Aptitude- 2 - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What is the General Aptitude-2 exam? |  |
| 2. How can I prepare for the General Aptitude-2 exam? |  |
| 3. What are some tips for improving numerical reasoning skills for the General Aptitude-2 exam? |  |
| 4. How can I enhance my verbal reasoning skills for the General Aptitude-2 exam? |  |
| 5. What strategies can I use for improving abstract reasoning abilities for the General Aptitude-2 exam? |  |





















