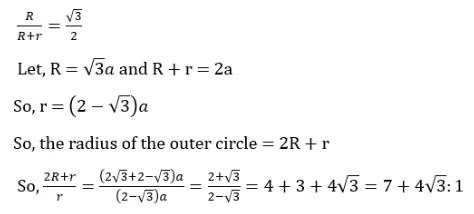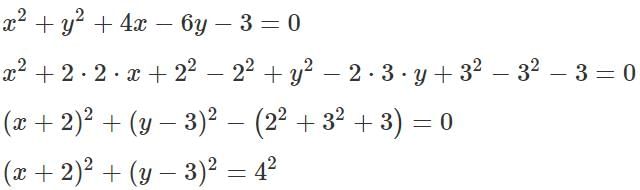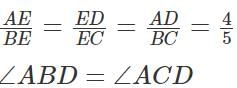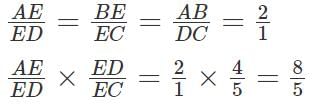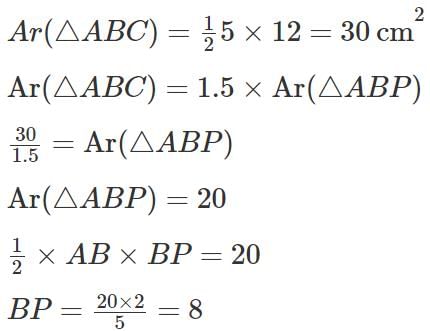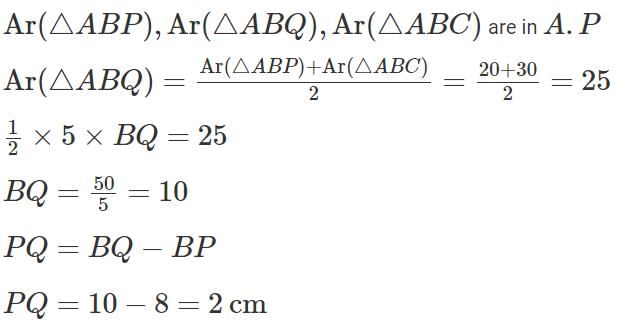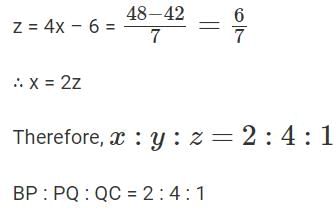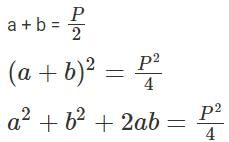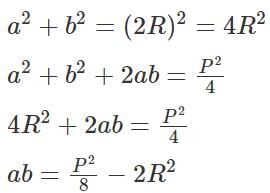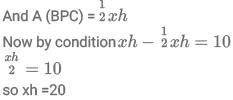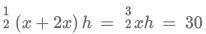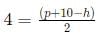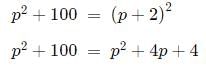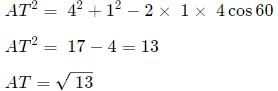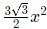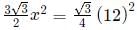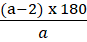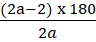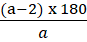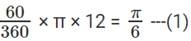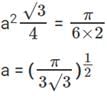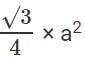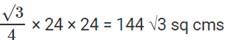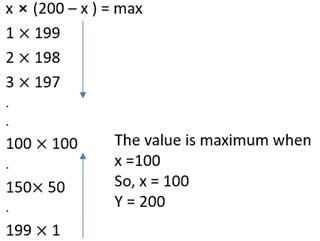Geometry CAT Previous Year Questions with Answer PDF
From 2017 to 2024, the CAT exam has included geometry questions focusing on properties of circles, triangles, quadrilaterals, and other polygons. These questions test concepts such as area calculations, angle relationships, and geometric properties, with a range of problem types from simple area computations to complex configurations involving tangents and inscribed shapes.
2024
Q1: An amount of Rs 10000 is deposited in bank A for a certain number of years at a simple interest of 5% per annum. On maturity, the total amount received is deposited in bank B for another 5 years at a simple interest of 6% per annum. If the interests received from bank A and bank B are in the ratio 10 : 13, then the investment period, in years, in bank A is
(a) 6
(b) 5
(c) 3
(d) 4
Ans: a
Sol:
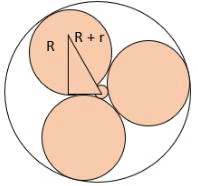
Q2: Three circles of equal radii touch (but not cross) each other externally. Two other circles, X and Y, are drawn such that both touch (but not cross) each of the three previous circles. If the radius of X is more than that of Y, the ratio of the radii of X and Y is
(a) 4 + 2√3 : 1
(b) 4 + √3 : 1
(c) 2 + √3 : 1
(d) 7 + 4√3 : 1
Ans: (d)
Sol: Let’s take the radius of the original circles to be R and that of the circle in between the three circles to be r …When we join the centers of the three circles, we will get an equilateral triangle of side length 2R. The distance between the smallest circle’s center and the biggest circle’s centre = R + r
Now, in the right angle triangle,Hence, option A is the required answer.
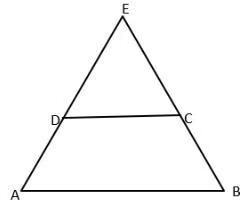
Q3: ABCD is a trapezium in which AB is parallel to CD. The sides AD and BC when extended, intersect at point E.
If AB = 2 cm, CD = 1 cm, and perimeter of ABCD is 6 cm, then the perimeter, in cm, of ∆AEB is
(a) 8
(b) 9
(c) 7
(d) 10
Ans: (a)
Sol:
Given,
AB = 2 and CD = 1 and, perimeter = 6
Let AD = x and CB = 3-x
So, AD + BC = 3
Triangle AEB and DEC are similar
So, the length of DE and CE will be x and 3-x respectively.
So, AE = 2x and BE = 6-2x
So, the perimeter AEB = 2x + 6-2x + 2 = 8cm
Hence, option A is the required answer.
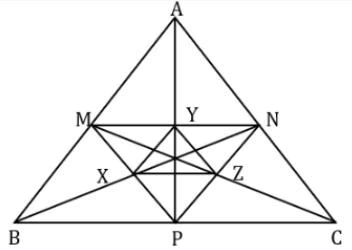
Q4: The midpoints of sides AB, BC, and AC in ∆ABC are M, N, and P, respectively. The medians drawn from A, B, and C intersect the line segments MP, MN and NP at X, Y, and Z, respectively. If the area of ∆ABC is 1440 sq cm, then the area, in sq cm, of ∆XYZ is
Ans: 90
Sol:
In geometry, the medians of a triangle divide the larger triangle into 6 smaller triangles of equal area.
Therefore, the Area of triangle MNP = 1/4 * (Area of triangle ABC) = ¼ *1440 = 360 sq. cm
Also, triangle XYZ is formed by joining the mid-points of triangle MNP.
Therefore, the area of triangle XYZ = ¼ * (area of triangle MNP) = ¼ * 360 = 90 sq.cm
Hence, 90 is the required answer.
2023
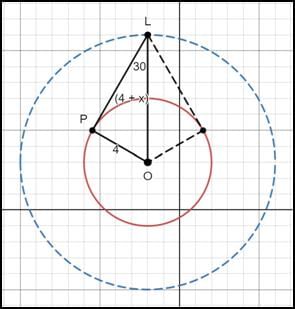
Q1: Let C be the circle x2 + y2 + 4x - 6y - 3 = 0 and L be the locus of the point of intersection of a pair of tangents to C with the angle between the two tangents equal to 60°. Then, the point at which L touches the line x = 6 is [2023]
(a) (6,4)
(b) (6,8)
(c) (6,3)
(d) (6,6)
Ans: c
Sol:
This is the equation of a circle with radius 4 units and centered at (-2, 3)
From a point L we drop two tangents on the circle such that the angle between the tangents is 60o.
Therefore the locus of the point L, is a circle centered at (-2, 3) and has a radius of (4 + x = 8) units.The equation of this locus is thus, (x + 2)2 + (y - 3)2 = 82
When X = 6, we have, (8)2 + (y - 3)2 = 82, that is y = 3
The circle, (x + 2)2 + (y - 3)2 = 82, touches the line x = 6 at (6, 3).
Q2: A quadrilateral ABCD is inscribed in a circle such that AB : CD = 2 : 1 and BC : AD = 5 : 4. If AC and BD intersect at the point E, then AE : CE equals [2023]
(a) 1 : 2
(b) 5 : 8
(c) 8 : 5
(d) 2 : 1
Ans: c
Sol:
∠DAC=∠DBC
(Angles subtended by the chord DC on the same side.)
∠ADB=∠ACB
(Angles subtended by the chord AB on the same side.)
∠AED=∠BEC
(Vertically Opposite angles.)
Therefore, △AED∼△BEC
(Angles subtended by the chord AD on the same side.)
∠BAC=∠BDC
(Angles subtended by the chord BC on the same side.)
∠AEB=∠DEC
(Vertically Opposite angles.)
Therefore, △AEB∼△DEC
Therefore, AE : EC = 8 : 5
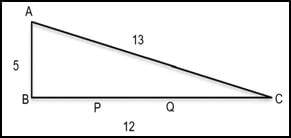
Q3: In a right-angled triangle ABC, the altitude AB is 5 cm, and the base BC is 12 cm. P and Q are two points on BC such that the areas of ΔABP, ΔABQ and ΔABC are in arithmetic progression. If the area of ΔABC is 1.5 times the area of ΔABP, the length of PQ, in cm, is [2023]
Ans: 2
Sol: The construction of the triangle according to the question is as follows:
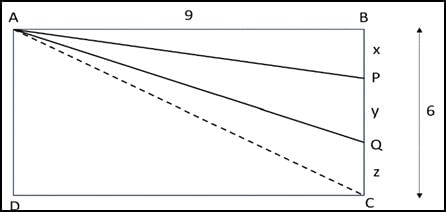
Q4: In a rectangle ABCD, AB = 9 cm and BC = 6 cm. P and Q are two points on BC such that the areas of the figures ABP, APQ, and AQCD are in geometric progression. If the area of the figure AQCD is four times the area of triangle ABP, then BP : PQ : QC is [2023]
(a) 1 : 1 : 2
(b) 1 : 2 : 4
(c) 2 : 4 : 1
(d) 1 : 2 : 1
Ans: c
Sol: Let BP = x, PQ = y and QC = z.
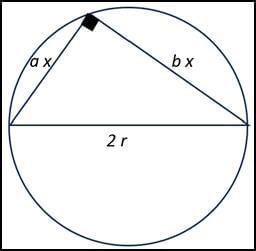
Q5: A triangle is drawn with its vertices on the circle C such that one of its sides is a diameter of C and the other two sides have their lengths in the ratio a : b. If the radius of the circle is r, then the area of the triangle is [2023]
(a) 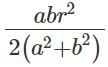
(b) 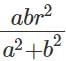
(c) 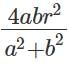
(d) 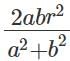
Ans: d
Sol: Since the angle subtended by the diameter on the circle is a right-angle, such a triangle inscribed in a circle with the diameter as one of its sides will be right angled.
“…and the other two sides have their lengths in the ratio a: b.”
Let the two sides be ax and bx.
2022
Q1: All the vertices of a rectangle lie on a circle of radius R . If the perimeter of the rectangle is P , then the area of the rectangle is [2022]
(a) 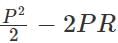
(b) 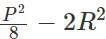
(c) 
(d) 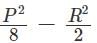
Ans: b
Sol:
Let the dimensions of the rectangle inscribed in the circle be a and b.
We are being asked to express the Area of the rectangle in terms of Perimeter and Radius.
Area of the rectangle = a * b
Perimeter, P = 2(a + b)
Since the vertices of the rectangle subtend right angle on the circle,
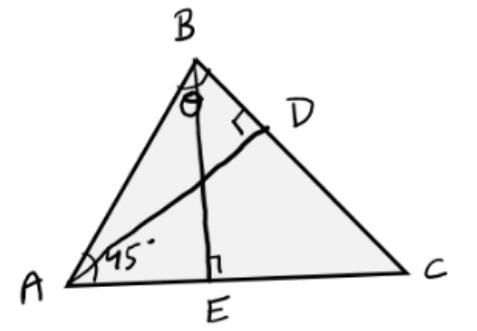
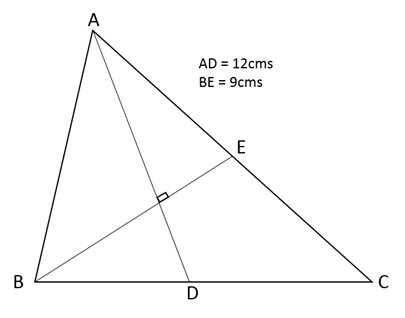
Q2: In triangle ABC, altitudes AD and BE are drawn to the corresponding bases. If ∠BAC = 45° and ∠ABC = θ, then AD/BE equals
(a) 1
(b) √2 cosθ
(c) 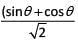
(d) 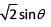
Ans: d
Sol:Let BE = 1
In △ABE, ∠ABE = 45º
So, AE = BE = 1
=> AB = √2
In △ABD, sin θ = AD/AB
=> AD = √2 sin θ
=> AD/BE = √2 sin θ
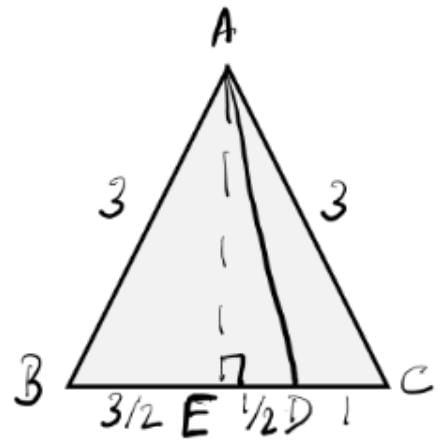
Q3: The length of each side of an equilateral triangle ABC is 3 cm. Let D be a point on BC such that the area of triangle ADC is half the area of triangle ABD. Then the length of AD. in cm, is
(a) √7
(b) √8
(c) √6
(d) √5
Ans: a
Sol:Ar(△ABD)/Ar(△ADC) = 2/1
=> BD : DC = 2 : 1 as height is same
BE = EC = 3/2
So, ED = 3/2 -1 = ½
In right △AEB, AE2 = AB2 – BE2 = 27/4
In right △AED, AD2 = AE2 + ED2 = 27/4 + 1/4 = 7So, AD = √7
Q4: Regular polygons A and B have number of sides in the ratio 1 : 2 and interior angles in the ratio 3 : 4. Then the number of sides of B equals
Ans: 10
Sol:
Q5: The lengths of all four sides of a quadrilateral are integer valued. If three of its sides are of length 1 cm, 2 cm and 4 cm, then the total number of possible lengths of the fourth side is
(a) 5
(b) 4
(c) 3
(d) 6
Ans: a
Sol:
Sum of any 3 sides of a triangle should be greater than the 4th side.
Case 1: When 4 is the largest side.
1 + 2 + x > 4
=> x > 1
Case 2: When x is the largest side.
1 + 2 + 4 > x
=> x < 7
So, 5 values of x are possible
Q6: Suppose the medians BD and CE of a triangle ABC intersect at a point O. If area of triangle ABC is 108 sq. cm., then, the area of the triangle EOD, in sq. cm., is
Ans: 9
Sol:
Ar(ABC) = 108
Ar(ABD) = 108/2 = 54
Ar(AED) = Ar(BED) = 54/2 = 27
In triangle BED, BO:OD = 2:1
So, area will also be in that ratio
So, Ar(EOD) = 27/3 = 9
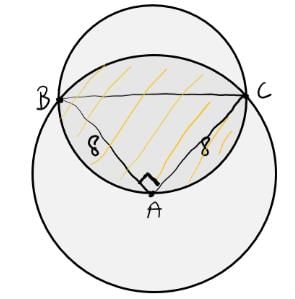
Q7: In a triangle ABC, AB = AC = 8 cm. A circle drawn with BC as diameter passes through A. Another circle drawn with center at A passes through B and C. Then the area, in sq. cm, of the overlapping region between the two circles is
(a) 16(π – 1)
(b) 32π
(c) 16π
(d) 32(π – 1)
Ans: d
Sol:
ABC will be a right-angled triangle inside the smaller circle as the 3 vertices lie on the circumference.
The shaded region = half the area of smaller circle (1) + the smaller segment BC of the bigger circle (2)
Radius of smaller circle = 8√2/2 = 4√2
(1) = π(4√2)2/2 = 16π
(2) = Area of sector ABC – area of triangle ABC = (90/360)π82 – (8*8)/2 = 16π – 32
(1) + (2) = 32(π – 1)
2021
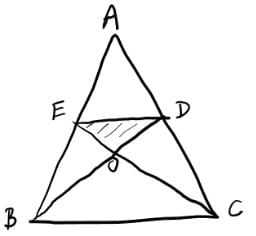
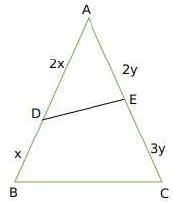
Q1: Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is
Ans: 30
Sol: We have :
Q2: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is
(a) 30
(b) 40
(c) 25
(d) 20
Ans: a
Sol: We are given that :Let DP =x
So AB =x
Now DP=CP
So CD = 2x
Now let height of trapezium be h
we can say A(Parallelogram ABPD ) = xhNow therefore area of trapezium ABCD =
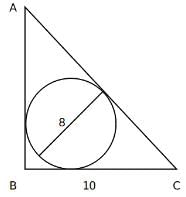
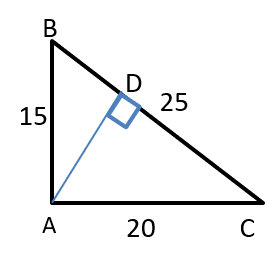
Q3: A circle of diameter 8 inches is inscribed in a triangle ABC where∠ABC=90∘. If BC = 10 inches then the area of the triangle in square inches is [2021]
Ans: 120
Sol:
We know that Inradius = (Perpendicular + Base − Hypotenuse) / 2
h - p = 2 or h = p + 2.
Now, p2 + 100 = h2
4p = 96
p = 24.
Hence, Area = 1/2 x 24 x 10 = 120
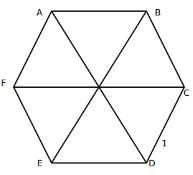
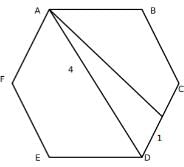
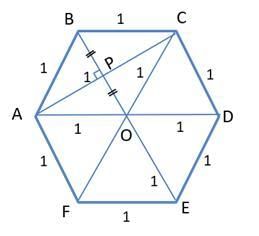
Q4: Suppose the length of each side of a regular hexagon ABCDEF is 2 cm.It T is the mid point of CD,then the length of AT, in cm, is [2021]
(a) √13
(b) √14
(c) √12
(d) √15
Ans: a
Sol:
Since a regular hexagon can be considered to be made up of 6 equilateral triangles, a line joining the farthest vertices of a hexagon can be considered to be made up using the sides of two opposite equilateral triangle forming the hexagon. Hence, its length should be twice the side of the hexagon, in this case, 4 cm.
Now, AD divided the hexagon into two symmetrical halves. Hence, AD bisects angle D, and hence, angle ADC is 60∘.
We can find out the value of AT using cosine formula:
Q5: If the area of a regular hexagon is equal to the area of an equilateral triangle of side 12 cm, then the length, in cm, of each side of the hexagon is [2021]
(a) 4√6
(b) 6√6
(c) √6
(d) 2√6
Ans: d
Sol: Area of a regular hexagon =
Area of an equilateral triangle =; where a = side of the triangle
Since the area of the two figures are equal, we can equate them as folllows:
On simplifying: x2 = 24
∴ x = 2√6
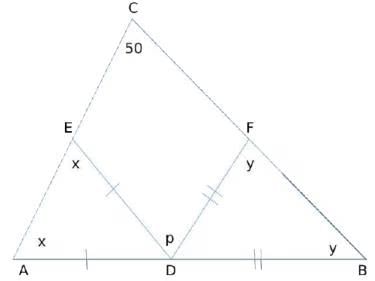
Q6: If a triangle ABC, 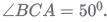 . D and E are points on AB and AC, respectively, such that AD = DE. If F is a point on BC such that BD = DF, then ∠FDE, in degrees, is equal to
. D and E are points on AB and AC, respectively, such that AD = DE. If F is a point on BC such that BD = DF, then ∠FDE, in degrees, is equal to
(a) 72
(b) 80
(c) 100
(d) 96
Ans: b
Sol:We need to find out p.
Angle ADE = 180 - 2x
Angle BDF = 180 - 2y
Now, 180 - 2y + p + 180 - 2x = 180 [Straight line = 180 deg]
p = 2x + 2y - 180
Also, x + y + 50 = 180 [Sum of the angles of triangle = 180]
x + y = 130
p = 260 - 180 = 80 degrees.
2019
Q1: AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to [2019]
(a) 8.5
(b) 9.3
(c) 9.1
(d) 7.8
Ans: c
Sol:
We know that angle APB = AQB = 90o
We know PB = 6, AB = 10 and AP = 2AQ
From using Pythagorean triplet, we find that AP = 8 cms
So, AQ = 4cms
AQ2 + QB2 = AB2
16 + QB2 = 100
QB2 = 84
QB = 9.3
Q2: In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths 12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is [2019]
(a) 80
(b) 68
(c) 72
(d) 78
Ans: c
Sol:
We know that intersection of two medians is called a Centroid
We know, a Centroid divides the median in the ratio 2:1
AD = 12cms,
AG = 8cms, GD = 4cms
And similarly, BG = 6cms, GE = 3cms
Now, area (ΔABE) can be easily found out
area (ΔABE) = 1 / 2 x BE X AG
area (ΔABE) = 1 / 2 x 9 x 8 = 36 cm2
area (ΔABE) = area (ΔBEC)
area (ΔABC) = 2 x 36 = 72 cm2
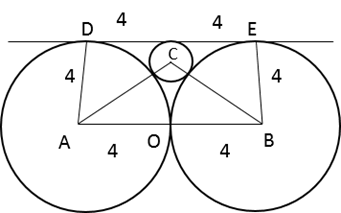
Q3: Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is [2019]
(a) π / 3
(b) 1
(c) 1 / √2
(d) √2
Ans: b
Sol:
For three circles to have a common tangent, the third circle must lie in between the two circles. Let the radius of the third circle be r cms
Now, Connect the centres of the circles with one another and with the intersection points. Let them be A,B,C,D,E respectively.
Now, from observing the constructed diagram, we find
AB = 8cms
AC = (4 + r) cms
BC = (4 + r) cms
OC = (4 - r) cms
Now, consider the right triangle OBC,
Applying Pythagoras theorem,
(4 + r)2 = 42 + (4 - r)2
16 + r2 + 8r = 16 + 16 + r2 - 8r
16r = 16
r = 1 cms
Q4: Let A and B be two regular polygons having a and b sides, respectively. If b = 2a and each interior angle of B is 3 / 2 times each interior angle of A, then each interior angle, in degrees, of a regular polygon with a + b sides is [2019 TITA]
Ans: 150
Sol: Sum of the interior angles of a n-sided Polygon = (n - 2) x 180
Measure of each interior angle =
So, Interior angle of the polygon with side a =
Interior angle of the polygon with side b =
It is given that interior angle of side b is 3 / 2 times to that of the polygon with side A= 3 / 2 x
(2a-2) x 180 = (3a - 6) x 180
2a - 2 = 3a - 6
a = 4
So, b = 8
(a + b) sides = 8 + 4 = 12 sides
Interior angle == 150°
Q5: Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is [2019]
(a) 10
(b) 8√2
(c) 6√2
(d) 5
Ans: a
Sol:
Now, the length of AP would be maximum, when AB = AC (ABC is an Isosceles Right Triangle)
So, AB = AC = 10√2cms
Applying Pythagoras theorem to ΔAPB, we get
AB2 = AP2 + PB2
(10√2)2 = 102 + x2
x2 = 100
x = 10 cms
2018
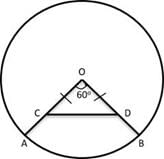
Q1: In a circle with centre O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is [2018]
(a) (π / 4)1 / 2
(b) (π / 6)1 / 2
(c) (π / 4√3)1 / 2
(d) (π / 3√3)1 / 2
Ans: d
Sol:
Given ∠AOB = 60°
Area of Sector AOB =
Given OC = OD => ∠OCD = ∠ODC = 60°
△OCD is an Equilateral Triangle with side = a
Area(△OCD) =
Its given that Area(OCD) = 1/2 × Area(OAB)
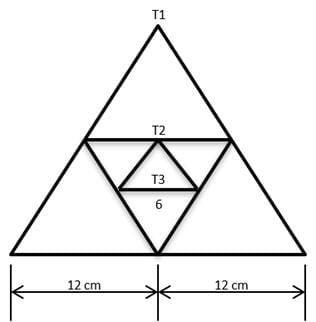
Q2: Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,... will be [2018]
(a) 192√3
(b) 164√3
(c) 248√3
(d) 188√3
Ans: a
Sol:
As the triangle progresses infinitely and the side length decreases, it follows an infinite GP series
As the sides decrease by half, their areas decrease by 1 / 4
We know, Area of an Equilateral Triangle =
Area of T1 =Sum of an Infinite GP = a / 1 − r where a = 144 √3 , r = 1 / 4
Sum of areas ( T1, T2, T3,..) =
Therefore, Sum of areas= 192 √3 sq cms.
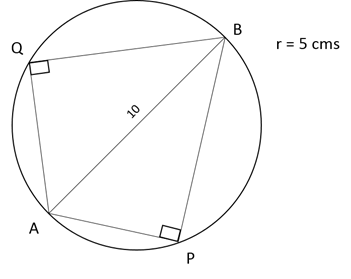
Q3: Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD? [2018]
(a) 25, 10
(b) 24, 12
(c) 25, 9
(d) 24, 10
Ans: d
Sol:
Since, ABCD is a rectangle inscribed inside a circle
ABC must be a Right triangle
Given that radius of Circle = 13 cms
5, 12, 13 forms a Pythagorean Triplet
10, 24, 26 is also a Pythagorean triplet
So, 10 and 24 are possible length and breadth of ABCD
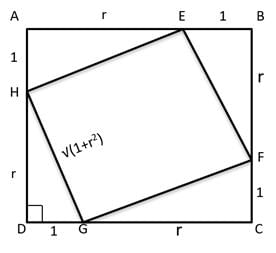
Q4: Points E, F, G, H lie on the sides AB, BC, CD, and DA, respectively, of a square ABCD. If EFGH is also a square whose area is 62.5% of that of ABCD and CG is longer than EB, then the ratio of length of EB to that of CG is: [2018]
(a) 1 : 3
(b) 4 : 9
(c) 2 : 5
(d) 3 : 8
Ans: a
Sol:
Given, Area(EFGH) = 62.5% Area(ABCD)
Area(EFGH) = 5 / 8 Area(ABCD)
Let EB = 1 and CG = r
Similarly, the rest other dimensions are also of lengths 1 or r units
Applying pythagoras theorem on △DHG we get GH = √(1 + r2)
Area(ABCD) = (1 + r)2 and Area(EFGH) = (√(1 + r2))2
=> (1 + r2) = 5 / 8(1 + r)2
1 + r2 = 5 / 8 (1 + r2 + 2r)
8 + 8r2 = 5 + 5r2 + 10r
3r2 – 10r + 3 = 0
(3r - 1) × (r - 3) = 0
r = 1 / 3 or r = 3
As CG > EB
r = 3 and ratio (EB : CG)= (1 : r) = (1 : 3)
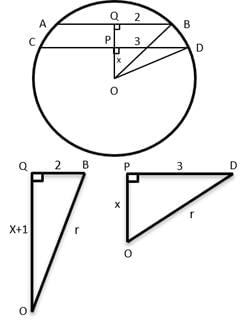
Q5: In a circle, two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm. If the distance between these chords is 1 cm, then the radius of the circle, in cm, is [2018]
(a) √13
(b) √14
(c) √11
(d) √12
Ans: a
Sol:
Given that Chords lie on the same side of diameter with lengths 4 cms and 6 cms
Draw a perpendicular from the origin to both the chords and mark the points of intersection as P and Q respectively
Consider radius of circle as ‘r’ and distance OP as ‘x’
Draw lines from origin to the end of the chord and mark the points as D and B respectively
Thus, △OQB and △OPD form a right Triangle
Applying Pythagoras Theorem on both triangles,
(x+1)2 +22 = r2 ---(1)
x2 +32 = r2 ---(2)
We find that there is an increase and decrease by 1 in both equations
So, x2 = 22 , x = 2
r2 = 22 + 32 = 4 + 9 = 13
r = √13 cms
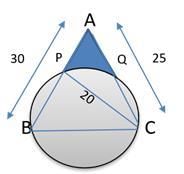
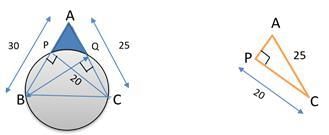
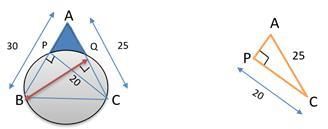
Q6: On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is [2018 TITA]
Ans: 24
Sol:
Let ABC be the triangle on which a circle of diameter BC is drawn, intersecting AB and AC at points P and Q respectively.The lengths of AB, AC and CP are 30cm, 25cm and 20 cm respectively we have to find the length of BQ in cm.
Key thing here is ,this is semicircle so this angle P and Q should be 90° and now we are looking to do Pythagoras theorem
So think about triangle PAC, by Pythagoras theorem
AC2 = AP2 + PC2 we can find that AP = 15
Since AP = 15 we can find BP by
AB = AP + PB
30 = 15 + PB
PB = 15
Now we can look at the triangle BPC, by Pythagoras theorem we can find that BC = 25
Now we have to find BQ .So we can take the area of the triangle formula which is equal to 1/2 × base × height
area of the triangle formula = 1/2 × base × height
1/2 × AB × PC = 1/2 × AC × BQ
1/2 × 30 × 20 = 1/2 × 25 × BQ
BQ = 24 cm
Q2: A chord of length 5 cm subtends an angle of 60° at the centre of a circle. The length, in cm, of a chord that subtends an angle of 120° at the centre of the same circle is [2018]
(a) 2π
(b) 5√3
(c) 6√2
(d) 8
Ans: b
Sol:
Given that a chord of length 5 cm subtends an angle of 60° at the centre of a circle.
We have to find the length of a chord that subtends an angle of 120° at the centre of the same circle
sin 60° = BC / OB
⟹ √3 / 2 = BC / 5
⟹ BC = 5√3 / 2 and AC = 5√3 / 2
So AB = 5√3 / 2 + 5√3 / 2 = 5√3
The length of a chord that subtends an angle of 120° at the centre of the same circle is 5√3
2017
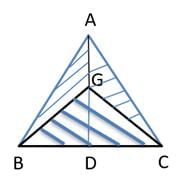
Q1: From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is: [2017]
(a) 225√3
(b) 500 / √3
(c) 275 / √3
(d) 250 / √3
Ans: b
Sol:
Given that from a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. Here GBC is the one third of the area of the triangle.
We can join AG and GD which is the median. Each of the shaded triangle has the same area and therefore the remaining area is two-thirds of ABC
The ratio of the sides are 8 : 5 : 7
Area of triangle = √(s(s − a)(s − b)(s − c))
where, semi perimeter (s) = 8 + 5 + 7 / 2 = 10
Area = √(10(10 − 8)(10 − 5)(10 − 7))
Area = √(10(2)(5)(3))
Area = 10√3
Area of ABC = 25 × 10 √3 (As 8 : 5 : 7 multiplied by 5 gives the sides of triangle ABC)
Therefore area of the remaining traingle = 2 / 3 × 250√3 = 500 / √3
Q2: Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is: [2017 TITA]
Ans: 24
Sol:
Given that ABC be a right-angled triangle with BC as the hypotenuse.
Lengths of AB and AC are 15 km and 20 km, respectively.
We have to find the minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour.
We should first find the minimum distance in order to find the minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour.
Therefore minimum distance AD has to be found and then it should be divided by the 30 km per hour.
Using the idea of similar triangles
Area of the triangle ABC
⟹ 1 / 2 × BA × AC = 1 / 2 × BC × AD
⟹ 1 / 2 × 15 × 20 = 1 / 2 × 25 × AD
⟹ AD = 12 units
Hence 12 kms is travelled at 30km per hour ⟹ 12 / 30 = 2 / 5
The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is 2 / 5 × 60 = 24 minutes
Key thing to be noted here is using Pythagoras theorem to find the altitude AD and then using Speed, Time and Distance formula to find the time.
Q3: Let ABCDEF be a regular hexagon with each side of length 1 cm. The area (in sq cm) of a square with AC as one side is [2017]
(a) 3√2
(b) 3
(c) 4
(d) √3
Ans: b
Sol:
Given that ABCDEF be a regular hexagon with each side of length of 1 cm.
We have to find the area of a square with AC as one side.
ABO is the equilateral triangle with each side having length of 1 cm and ABCO is the rhombus.
Altitude of an equilateral triangle = √3/2 a
So AP = √3/2 × 1
Where AP = PC
⟹ AC = AP + PC
⟹ AC = √3 / 2 × 2
⟹ AC = √3
Area of a square = a2 sq.units
Area of the square with AC as one side = √3 × √3 = 3 sq.units
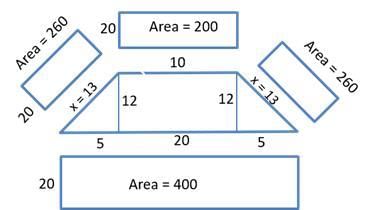
Q4: The base of a vertical pillar with uniform cross section is a trapezium whose parallel sides are of lengths 10 cm and 20 cm while the other two sides are of equal length. The perpendicular distance between the parallel sides of the trapezium is 12 cm. If the height of the pillar is 20 cm, then the total area, in sq cm, of all six surfaces of the pillar is [2017]
(a) 1300
(b) 1340
(c) 1480
(d) 1520
Ans: c
Sol:
We have to find the total area of all six surfaces of the pillar which is 4 rectangles + 2 trapeziums one at the top and one at the bottom
Area of the rectangle = b × h
⟹ Area of rectangle with l = 20 b = 10
⟹ Area = 200 sq.cm
⟹ Area of rectangle with l = 20 b = 20
Area = 400 sq.cm
⟹ Area of 2 rectangles with l = 20 b = 13 is 2 × 13 × 20 = 520 sq. cm
Sum of areas of 4 rectangles = 520 + 200 + 400 = 1120 sq.cm
Area of the trapezium = 1/2 × 12 (10 + 20)
Area of the trapezium = 6 × 30 = 180 sq.cm
Area of both the trapezium = 2 × 180 = 360 sq.cm
Sum of areas of 4 rectangles = 1120 sq.cm.
Area of both the trapezium = 360 sq.cm
Total surface area of the pillar = 4 rectangles + 2 trapeziums
Total surface area of the pillar = 1120 + 360
Total surface area of the pillar = 1480 sq.cm
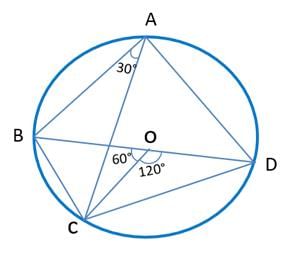
Q5: ABCD is a quadrilateral inscribed in a circle with centre O. If ∠COD = 120 degrees and ∠BAC = 30 degrees, then the value of ∠BCD (in degrees) is [2017 TITA]
Ans: 90
Sol:
ABCD is a quadrilateral inscribed in a circle with centre O.
∠COD = 120°
∠BAC = 30°
∠BOC = 60° (twice that of ∠BAC)
BOD is a straight line (60 + 120) = 180° or BD is the diameter of the circle
∠BOD = 180°
We have to find the value of ∠BCD
∠BCD is an angle in a semicircle = 90°
Q6: If three sides of a rectangular park have a total length 400 ft., then the area of the park is maximum when the length (in ft.) of its longer side is [2017 TITA]
Ans: 200
Sol:
Given that the three sides of a rectangular park have a total length 400ft
i.e. 2x + y = 400 ft
xy should be maximum
y = 400 – 2x
x × (400 – 2x) = max
x × (200 – x) = max
Let us check for different values
The area of the park is maximum when x = 100 and y = 200.
The length of the longer side y is equal to 200 ft.
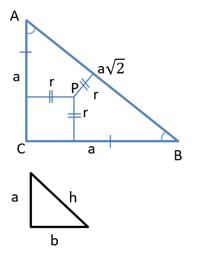
Q7: Let P be an interior point of a right-angled isosceles triangle ABC with hypotenuse AB. If the perpendicular distance of P from each of AB, BC, and CA is 4(√2 - 1) cm, then the area, in sq. cm, of the triangle ABC is [2017 TITA]
Ans: 16
Sol:
Let ABC be the right angled isosceles triangle with hypotenuse AB and P be an interior point
r (inradius) = 4(√2 - 1)
In any right triangle with a , b , h being its sides, r = a+b−h / 2
Here we have the right angled isosceles triangle with a , a , a√2 as its sides
⟹ a / √2 = 4
⟹ a = 4√2
⟹ The area of the triangle ABC = 1 / 2 × 4√2 × 4√2
The area of the triangle ABC = 16 sq.cm
|
174 videos|243 docs|95 tests
|
FAQs on Geometry CAT Previous Year Questions with Answer PDF
| 1. What are the basic principles of geometry? |  |
| 2. How is geometry used in real life? |  |
| 3. What is the importance of geometry in mathematics? |  |
| 4. What are the different types of angles in geometry? |  |
| 5. How can I improve my geometry skills? |  |