Geometry Questions with Answer- 3 | General Aptitude for GATE - Mechanical Engineering PDF Download
Question 21: Rhombus of side 6 cm has an angle equal to the external angle of a regular octagon. Find the area of the rhombus.
A. 18√2 cm2
B. 9√2 cm2
C. 15√2 cm2
D. 12√2 cm2
Answer. 18√2 cm2
Explanation.
Side of the rhombus 's' = 6 cm
Angle between sides 'a' = exterior angle of an octagon
Therefore a = 45 degrees
Area of rhombus = sin a * s2
Area = (1/√2) * 36
Area = 18√2 cm2
The question is "Find the area of the rhombus."
Hence, the answer is 18√2 cm2.
Choice A is the correct answer.
Question 22: A circle inscribed in a square of side 2 has an equilateral triangle inscribed inside it. What is the ratio of areas of the equilateral triangle to that of the square?
A. 9√3 : 16
B. 3√3 : 4
C. 9√3 : 4
D. 3√3 : 16
Answer. 3√3 : 16
Explanation
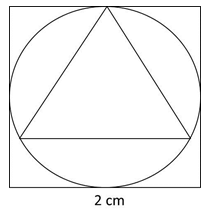
The radius of the circle is 1 unit.
If we considered the side of the equilateral triangle to be ‘a’, the circumradius of an equilateral triangle is 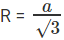
Therefore, a = √3
So, ratio of areas of the equilateral triangle to that of the square is
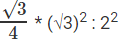
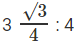
3√3 : 16
The question is "What is the ratio of areas of the equilateral triangle to that of the square? "
Hence, the answer is 3√3 : 16 Units
Choice D is the correct answer.
Question 23: An acute-angled isosceles triangle has two of its sides equal to 10 and 16. Find the area of this triangle.
A. √231 units
B. 12√66 units
C. 24 units
D. 5√231 units
Answer. 5√231 units
Explanation.
The third side is either 10 or 16 and the sum of the squares of the two smaller sides must be greater than the square of the third side.
102 + 102 < 162
Therefore, the third side of the triangle is 16.
Semiperimeter, S = (10 + 16 + 16)/2 = 21
Area = √(21(21−16)(21−16)(21−10))
= √(21 * 5 * 5 * 11)
= 5√231 units
The question is "Find the area of this triangle."
Hence, the answer is 5√231 units.
Choice D is the correct answer.
Question 24: Three equal circles are placed inside an equilateral triangle such that any circle is tangential to two sides of the equilateral triangle and to two other circles. What is the ratio of the areas of one circle to that of the triangle
A. π : (6+4√3)
B. 3π : (6+4√3)
C. 2π : (6+4√3)
D. π : (6+2√3)
Answer. π : (6+4√3)
Explanation.
Let radii of each circle be ‘a’.
Distance PQ = 2a.
Draw PM perpendicular to AB
∠MAP = 30°
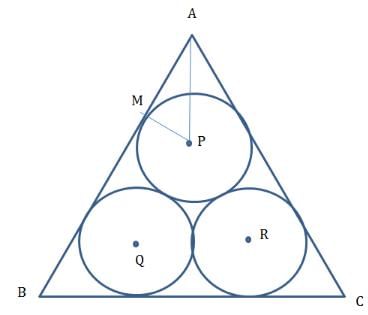
MP = a , AM = a3
After this we are done.
Area of circle = πa2
Area of equilateral triangle 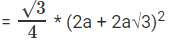
= a2 (6+4√3)
Ratio = π : (6+4√3)
The question is "What is the ratio of the areas of one circle to that of the triangle?"
Hence, the answer is π : (6+4√3)
Choice A is the correct answer.
Question 25: There is an equilateral triangle with a square inscribed inside it. One of the sides of the square lies on a side of the equilateral △. What is the ratio of the area of the square to that of the equilateral triangle?
A. √3 : (5 + 4√3)
B. 2√3 : (7 + 4√3)
C. 4√3 : (7 + 4√3)
D. 4√3 : (5 + 2√3)
Answer. 4√3 : (7 + 4√3)
Explanation.
Let side of square be ‘a’
MN = LP = a
∠ABC = 60°
ML = a. BL  (Use some trigonometry for this)
(Use some trigonometry for this)
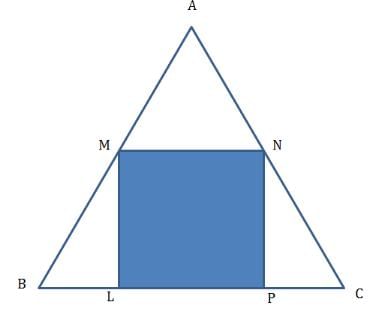
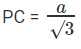
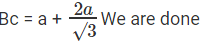
Area of square = a2
Area of equilateral triangle
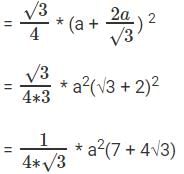
Ratio = 4√3 : (7 + 4√3)
The question is "What is the ratio of the area of the square to that of the equilateral triangle?"
Hence, the answer is 4√3 : (7 + 4√3)
Choice C is the correct answer.
Question 26: Consider Square S inscribed in circle C, what is the ratio of the areas of S and Q? And, Consider Circle C inscribed in Square S, what is the ratio of the areas of S and Q?
A. 2:π, 4:π
B. 4:π, 2:π
C. 1:π, 4:π
D. 2:π, 1:π
Answer. 2:π, 4:π
Explanation.
If square is inside the circle, ratio of areas of square to that of circle is 2 : π.
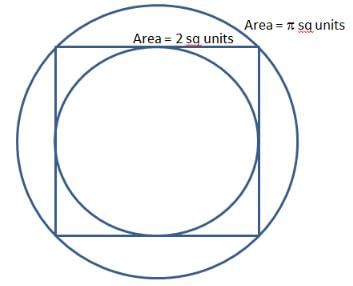
If circle is inside square, ratio of areas of square to that of circle is 4 : π.
Remember, circle area goes with π, square area goes with number.
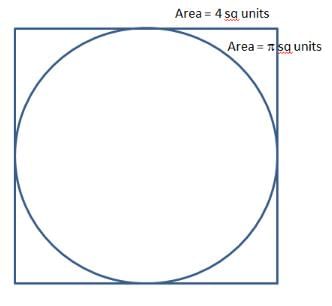
If square is inside the circle, ratio of areas of square to that of circle is 2 : π.
If circle is inside square, ratio of areas of square to that of circle is 4 : π.
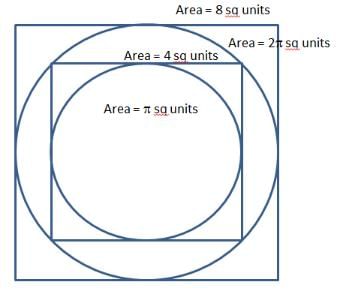
The question is "What is the ratio of the areas of S and Q? and what is the ratio of the areas of S and Q?"
Hence, the answer is 2:π, 4:π.
Choice A is the correct answer.
Question 27: Consider equilateral triangle T inscribed in circle C, what is ratio of the areas of T and C? Consider Circle C inscribed in equilateral triangle T, what is ratio of the areas of T and C?
A. 3√3:π , 3√3:16π
B. 3√3:4π , 3√3:π
C. √3:π , 3√3:4π
D. √3:π , √3:16π
Answer. 3√3:4π , 3√3:π
Explanation.
For any equilateral triangle of side ‘a’
Inradius = 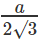 and circumradius =
and circumradius = 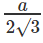

Area of equilateral triangle 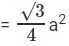
Area of smaller circle 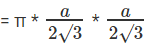
Area of larger circle 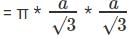
When Equilateral triangle T inscribed in circle C,
Ratio of Areas of T and C :: 3√3:4π
When Circle C inscribed in equilateral triangle T,
Ratio of Areas of T and C :: 3√3:π
The question is "Consider equilateral triangle T inscribed in circle C, what is ratio of the areas of T and C? Consider Circle C inscribed in equilateral triangle T, what is ratio of the areas of T and C? "
Hence, the answer is 3√3:4π , 3√3:π
Choice B is the correct answer.
Question 28: Consider Regular Hexagon H inscribed in circle C, what is ratio of the areas of H and C? Consider Circle C inscribed in Regular Hexagon H, what is ratio of the areas of H and C?
A. 2√3 : 3π , 3√3 : 4π
B. 3√3 : π , 3√3 : 4π
C. 3√3 : 2π, 2√3 : π
D. √3 : π , √3 : 4π
Answer. 3√3 : 2π, 2√3 : π
Explanation.
Inradius = altitude of equilateral triangle of side a = √3a/2

Circumradius = a.
Area of regular hexagon = 6 * √3a2/4
Area of smaller circle = π ∗ √3a/2 ∗ √3a/2 = 3πa2/4
Area of larger circle = πa2
When Hexagon H inscribed in circle C,
Ratio of Areas of H and C :: 3√3 : 2π
When Circle C inscribed in Regular Hexagon H,
Ratio of Areas of H and C :: 2√3 : π
The question is "Consider Regular Hexagon H inscribed in circle C, what is ratio of the areas of H and C? Consider Circle C inscribed in Regular Hexagon H, what is ratio of the areas of H and C?"
Hence, the answer is 3√3 : 2π, 2√3 : π.
Choice C is the correct answer.
Question 29: What is the distance between the orthocentre and the circumcenter of a triangle who sides measure 24 cm, 26 cm and 10 cm?
A. 13 cm
B. 12 cm
C. 7.5 cm
D. √30 cm
Answer. 13 cm
Explanation.
The sides measure 24 cm, 26 cm and 10 cm. 10, 24, 26 is a Pythagorean triple!
So it is a right angled triangle we are talking about.
Draw the perpendicular bisectors to get the circumcenter. Orthocenter is the point where all altitudes meet.
In a right angled triangle it is the vertex that makes 90 deg angle.
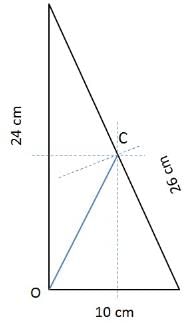
Now it is easy to find OC! It is the length of the diagonal of the rectangle formed.
Length = 12 cm, breadth = 5 cm
Diagonal = √(122+52) = 13
The question is "What is the distance between the orthocentre and the circumcenter of a triangle who sides measure 24 cm, 26 cm and 10 cm?"
Hence, the answer is 13 cm.
Choice A is the correct answer.
Question 30: Two circles with centres O1 and O2 touch each other externally at a point R. AB is a tangent to both the circles passing through R. P’Q’ is another tangent to the circles touching them at P and Q respectively and also cutting AB at S. PQ measures 6 cm and the point S is at distance of 5 cms and 4 cms from the centres of the circles. What is the area of the triangle SO1O2?
A. 9 cm2
B. 3(4+√7)/2 cm2
C. 27/2 cm2
D. (3√41)/2 cm2
Answer. 3(4+√7)/2 cm2
Explanation.
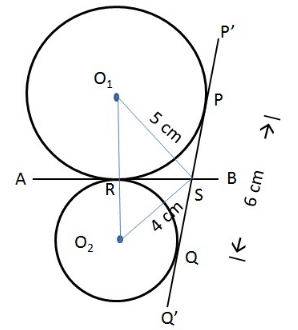
From the diagram we see that SP, SR are tangents to circle1 from same point S. Similarly SR, SQ are tangents from same point to circle 2.
SP = SR; SQ = SR implies SP = SQ
Given PQ = 6cm
SP + SQ = 6
Therefor SR = SP = SQ = 3 cm.
SR is the altitude to the triangle SO1O2. We need to find the length of the base O1O2 to determine the area.
O1RS is a right angled triangle with hypotenuse = 5 and one side = 3
Therefore, O1R = √(52 - 32) = 4cm
Similarly, O2RS is a right angled triangle with hypotenuse = 4 and one side = 3
Therefore, O2R = √(42 - 32) = √7cm
O1O2 = O1R + O2R = 4 + √7
Area of the triangle SO1O2 = 1/2 * SR * O1O2 = 1/2 * 3 * (4 + √7) cm2
The question is " What is the area of the triangle SO1O2?"
Hence, the answer is 3(4+√7)/2 cm2.
Choice B is the correct answer.
|
194 videos|168 docs|152 tests
|
FAQs on Geometry Questions with Answer- 3 - General Aptitude for GATE - Mechanical Engineering
| 1. What are the basic principles of geometry? |  |
| 2. How is geometry used in real life? |  |
| 3. What is the Pythagorean theorem? |  |
| 4. How do you calculate the area of a circle? |  |
| 5. What is the difference between congruent and similar figures? |  |





















