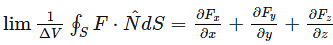Gradient, Divergence, and Curl | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Gradient |

|
| The divergence |

|
| The curl |

|
| The ∇ (del) operator |

|
| Interpretation |

|
| The Maxwell equations |

|
| Solved Numericals |

|
Gradient
The gradient of a scalar function f : Rn → R is a vector field of partial derivatives. In R2, we have: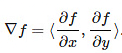 It has the interpretation of pointing out the direction of greatest ascent for the surface z = f(x,y)
It has the interpretation of pointing out the direction of greatest ascent for the surface z = f(x,y)We move now to two other operations, the divergence and the curl, which combine to give a language to describe vector fields in R3.
The divergence
Let F : R3 → R3 = ⟨Fx, Fy, Fz⟩ be a vector field. Consider now a small box-like region, R, with surface, S, on the cartesian grid, with sides of length Δx, Δy, and Δz with (x,y,z) being one corner. The outward pointing unit normals are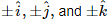 .
.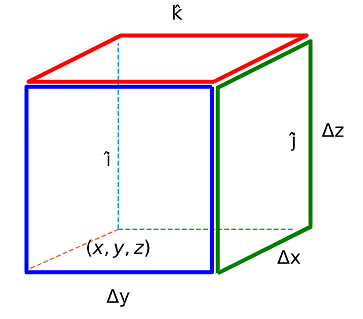
Consider the sides with outward normal 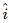 . The contribution to the surface integral,
. The contribution to the surface integral, 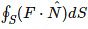 , could be approximated by
, could be approximated by
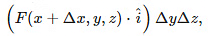
whereas, the contribution for the face with outward normal −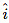 could be approximated by:
could be approximated by:
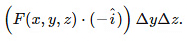
The functions are being evaluated at a point on the face of the surface. For Riemann integrable functions, any point in a partition may be chosen, so our choice will not restrict the generality.
The total contribution of the two would be:
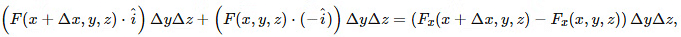
Were we to divide by ΔV = ΔxΔyΔzand take a limit as the volume shrinks, the limit would be ∂F/∂x.
If this is repeated for the other two pair of matching faces, we get a definition for the divergence:
The divergence of a vector field F : R3→R3 is given by divergence(F) =
The limit expression for the divergence will hold for any smooth closed surface, S, converging on (x, y, z) not just box-like ones.
General n
The derivation of the divergence is done for n = 3, but could also have easily been done for two dimensions (n = 2) or higher dimensions n > 3. The formula in general would be: for F(x1, x2,…, xn):Rn→ Rn.
The curl
Before considering the curl for n = 3 we derive a related quantity in n = 2. The "curl" will be a measure of the microscopic circulation of a vector field. To that end we consider a microscopic box-region in R2:
Let F = ⟨Fx, Fy⟩. For small enough values of Δx and Δy the line integral, ∮CF⋅d → r can be approximated by 4 terms:
The Riemann approximation allows a choice of evaluation point for Riemann integrable functions, and the choice here lends itself to further analysis. Were the above divided by ΔxΔy, the area of the box, and a limit taken, partial derivatives appear to suggest this formula: 
The scalar function on the right hand side is called the (two-dimensional) curl of F and the left-hand side lends itself as a measure of the microscopic circulation of the vector field, F : R2 → R2.
The ∇ (del) operator
The divergence, gradient, and curl all involve partial derivatives. There is a notation employed that can express the operations more succinctly. Let the Del operator be defined in Cartesian coordinates by the formal expression:
This is a vector differential operator that acts on functions and vector fields through the typical notation to yield the three operations:
Interpretation
The divergence and curl measure complementary aspects of a vector field. The divergence is defined in terms of flow out of an infinitesimal box, the curl is about rotational flow around an infinitesimal area patch.Let F(x, y, z)=[x, 0, 0], a vector field pointing in just the 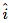 direction. The divergence is simply 1. If V is a box, as in the derivation, then the divergence measures the flow into the side with outward normal -
direction. The divergence is simply 1. If V is a box, as in the derivation, then the divergence measures the flow into the side with outward normal -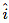 and through the side with outward normal which will clearly be positive as the flow passes through the region V, increasing as x increases, when x> 0.
and through the side with outward normal which will clearly be positive as the flow passes through the region V, increasing as x increases, when x> 0.
The radial vector field 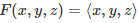 is also an example of a divergent field. The divergence is:
is also an example of a divergent field. The divergence is:
3
There is a constant outward flow, emanating from the origin. Here we picture the field when z = 0:
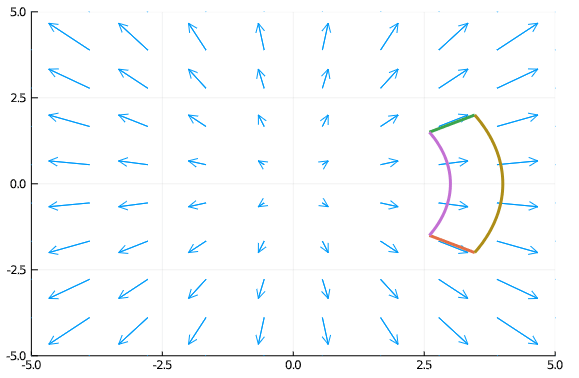
Consider the limit definition of the divergence:
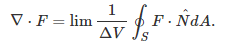
In the vector field above, the shape along the curved edges has constant magnitude field. On the left curved edge, the length is smaller and the field is smaller than on the right. The flux across the left edge will be less than the flux across the right edge, and a net flux will exist. That is, there is divergence.
Now, were the field on the right edge less, it might be that the two balance out and there is no divergence. This occurs with the inverse square laws, such as for gravity and electric field:
0
The vector field F(x,y,z)=⟨−y,x,0⟩ is an example of a rotational field. It's curl can be computed symbolically through:
curl([-y, x, 0], [x, y, z]) =
This vector field rotates as seen in this figure showing slices for different values of z: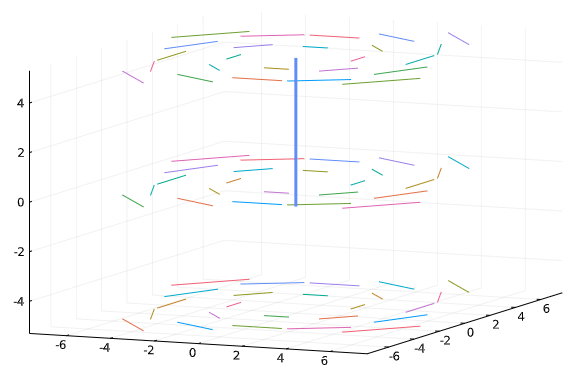 The field has a clear rotation about the z axis (illustrated with a line), the curl is a vector that points in the direction of the right hand rule as the right hand fingers follow the flow with magnitude given by the amount of rotation.
The field has a clear rotation about the z axis (illustrated with a line), the curl is a vector that points in the direction of the right hand rule as the right hand fingers follow the flow with magnitude given by the amount of rotation.
This is a bit misleading though, the curl is defined by a limit, and not in terms of a large box. The key point for this field is that the strength of the field is stronger as the points get farther away, so for a properly oriented small box, the integral along the closer edge will be less than that along the outer edge.
Consider a related field where the strength gets smaller as the point gets farther away but otherwise has the same circular rotation pattern
=
The Maxwell equations
The divergence and curl appear in Maxwell's equations describing the relationships of electromagnetism. In the formulas below the notation is E is the electric field; B is the magnetic field; ρ is the charge density (charge per unit volume); J the electric current density (current per unit area); and ϵ0, μ0, and c are universal constants.The equations in differential form are:
Gauss's law: ∇ ⋅ E = ρ/ϵ
That is, the divergence of the electric field is proportional to the density. We have already mentioned this in integral form.
Gauss's law of magnetism: ∇ ⋅ B = 0
The magnetic field has no divergence. This says that there no magnetic charges (a magnetic monopole) unlike electric charge, according to Maxwell's laws.
Faraday's law of induction: ∇ × E = −∂B/∂t
The curl of the time-varying electric field is in the direction of the partial derivative of the magnetic field. For example, if a magnet is in motion in the in the z axis, then the electric field has rotation in the x − y plane induced by the motion of the magnet.
Ampere's circuital law: ∇ × B = μ0J + μ0ϵ0∂E/∂t
The curl of the magnetic field is related to the sum of the electric current density and the change in time of the electric field.
In a region with no charges (ρ = 0) and no currents  , such as a vacuum, these equations reduce to two divergences being 0: ∇⋅E = 0 and ∇ ⋅ B = 0; and two curl relationships with time derivatives:
, such as a vacuum, these equations reduce to two divergences being 0: ∇⋅E = 0 and ∇ ⋅ B = 0; and two curl relationships with time derivatives: 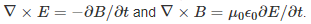 We will see later how these are differential forms are consequences of related integral forms.
We will see later how these are differential forms are consequences of related integral forms.
Solved Numericals
Q1. If  inferior vector is,
inferior vector is, 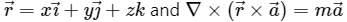 and
and
Solution: If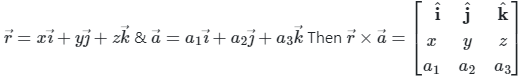

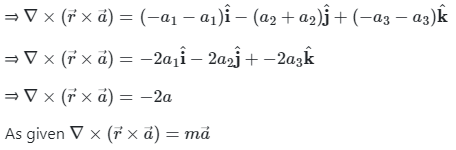
⇒ m = -2
Q2. What is the divergence of the vector field 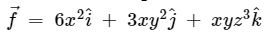 at the point (2, 3, 4).
at the point (2, 3, 4).
Solution: Divergence of the vector function:
The net outward flux from a volume element around a point is a measure of the divergence of the vector field at that point.
Divergence of a function 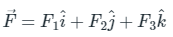
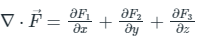
Calculation:
Given that,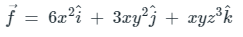
Therefore, the divergence of a given vector is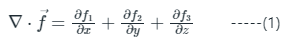
Here,
f1 = 6x2, f2 = 3xy2, f3 = xyz3
Therefore, from equation (1)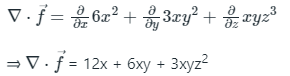
Therefore, divergence at point (2, 3, 4)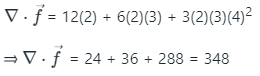
Q3: Find grad(f) if f(x, y, z) = xy + y2 z at the point (0, 1, -1)?
Solution: If F = f(x, y, z) then,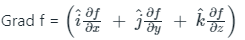
Calculation:
We have,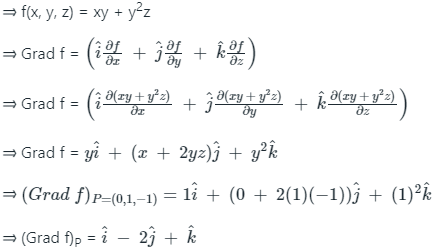
∴ If f(x, y, z) = xy + y2 z at the point (0, 1, -1) then grad f is 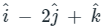
|
44 videos|109 docs|58 tests
|
FAQs on Gradient, Divergence, and Curl - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What are the key operators used in understanding the Maxwell equations? |  |
| 2. How is the gradient operator used in the Maxwell equations? |  |
| 3. What does the divergence operator signify in the context of mechanical engineering? |  |
| 4. How is the curl operator interpreted in the Maxwell equations? |  |
| 5. How is the ∇ (del) operator utilized in mechanical engineering when analyzing electromagnetic phenomena? |  |