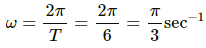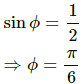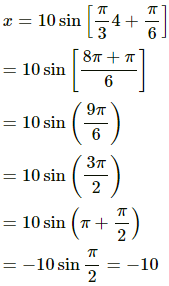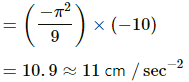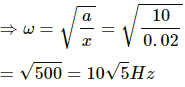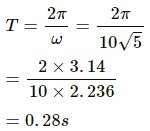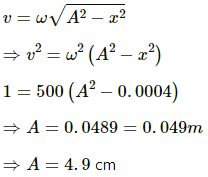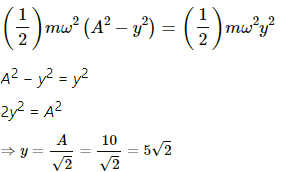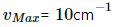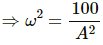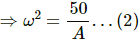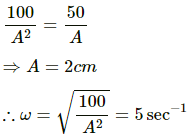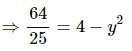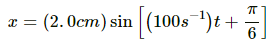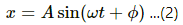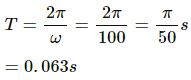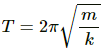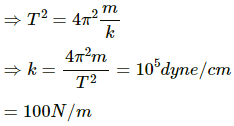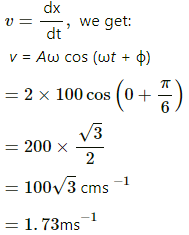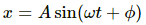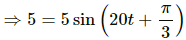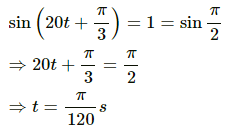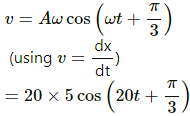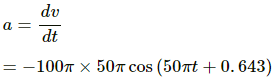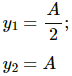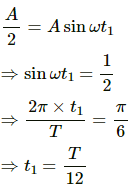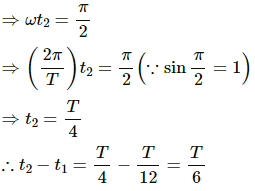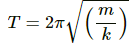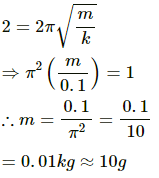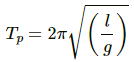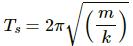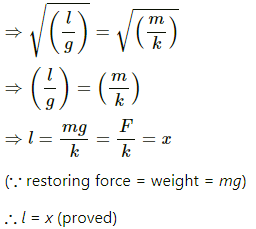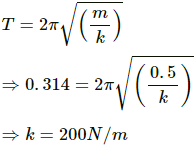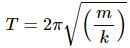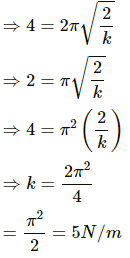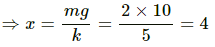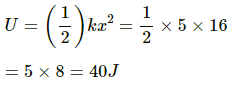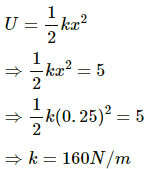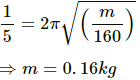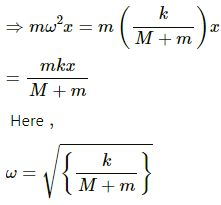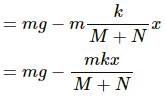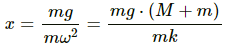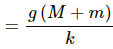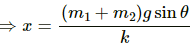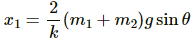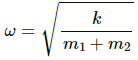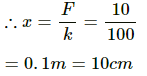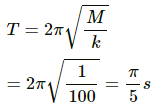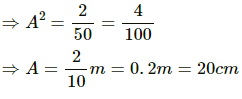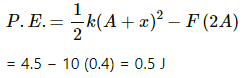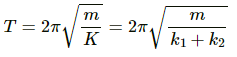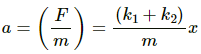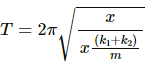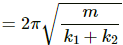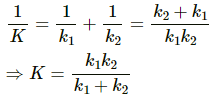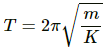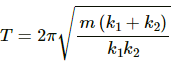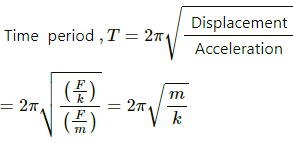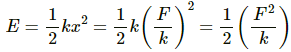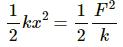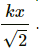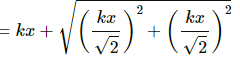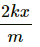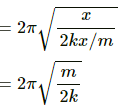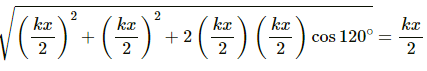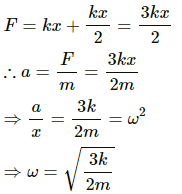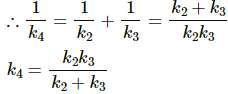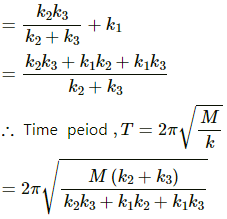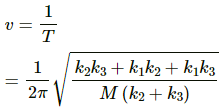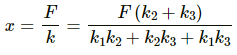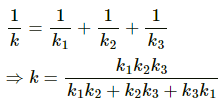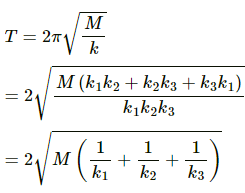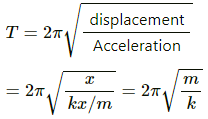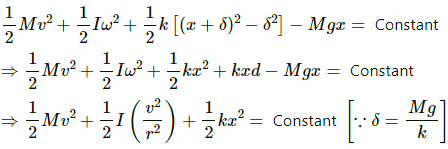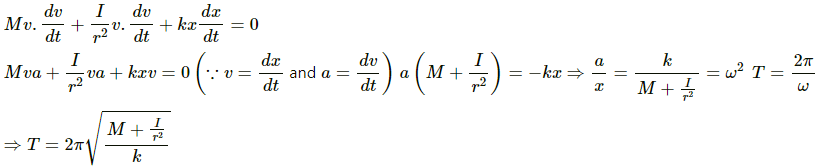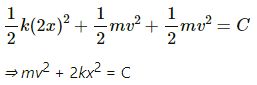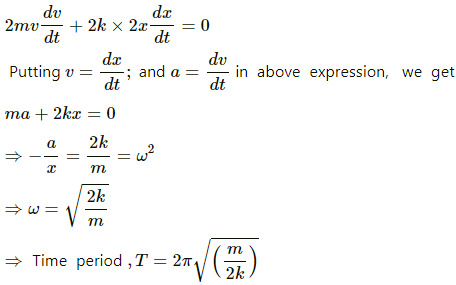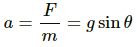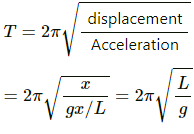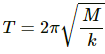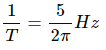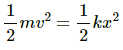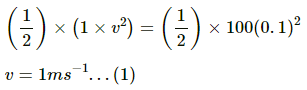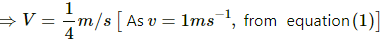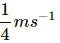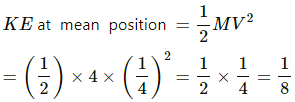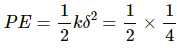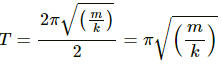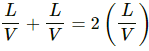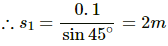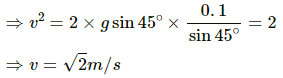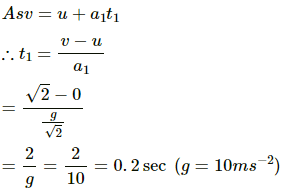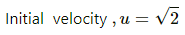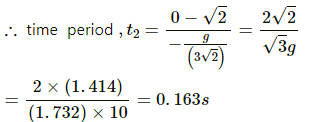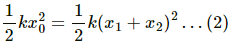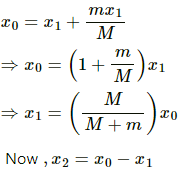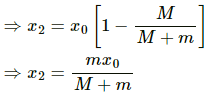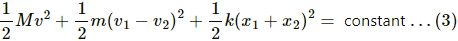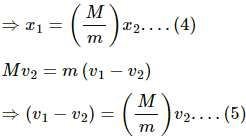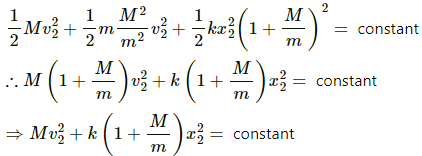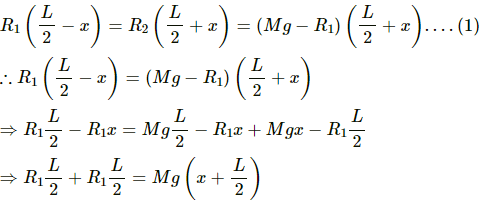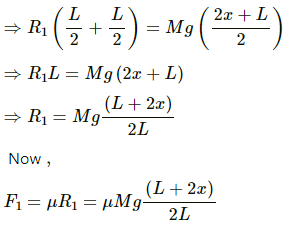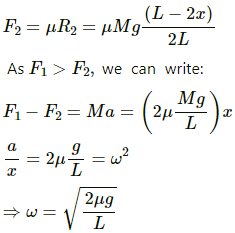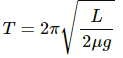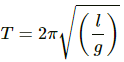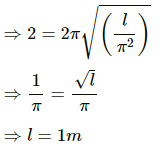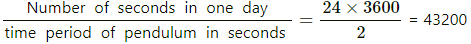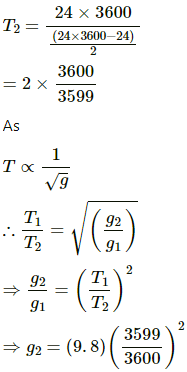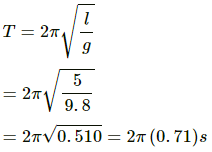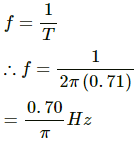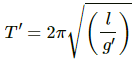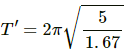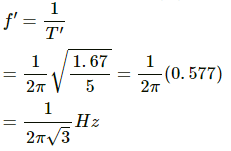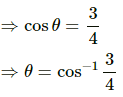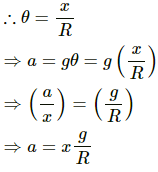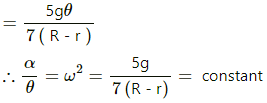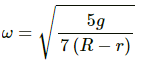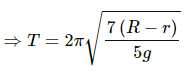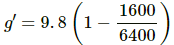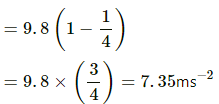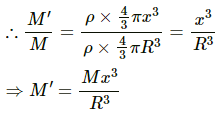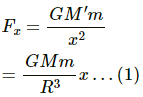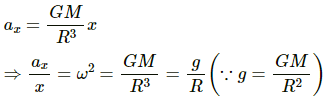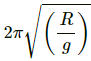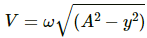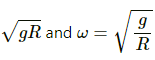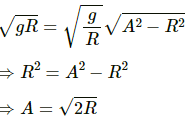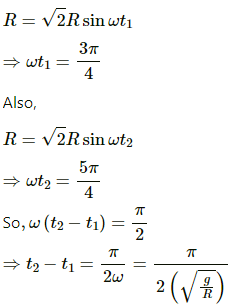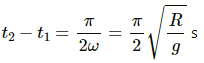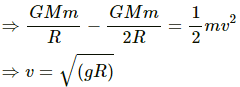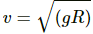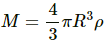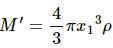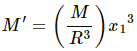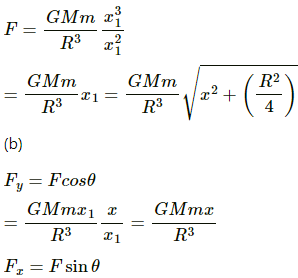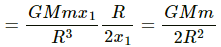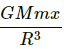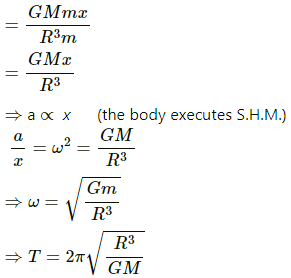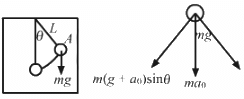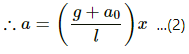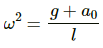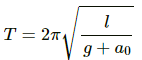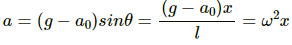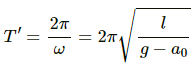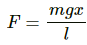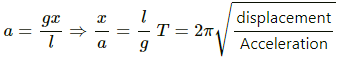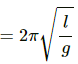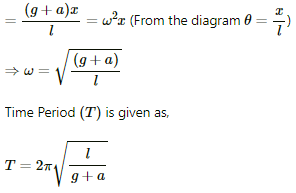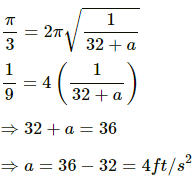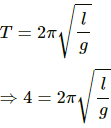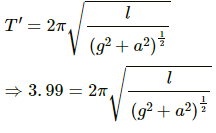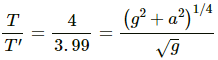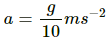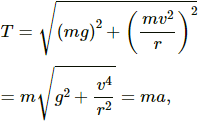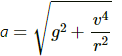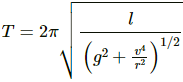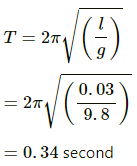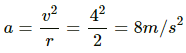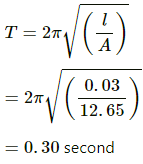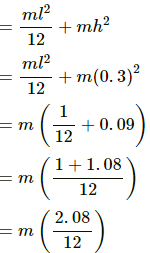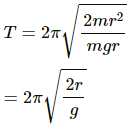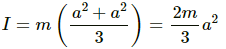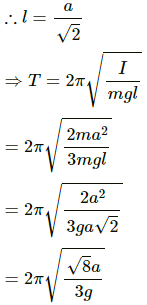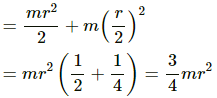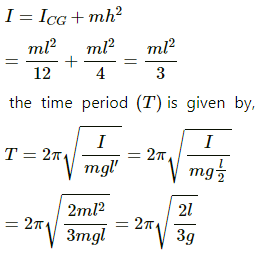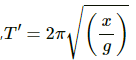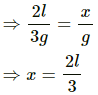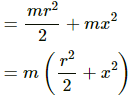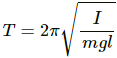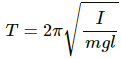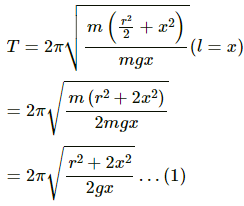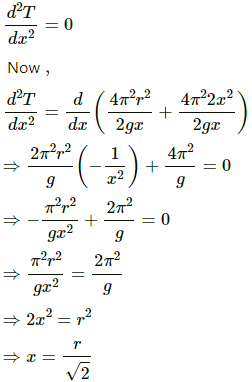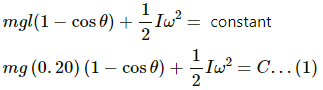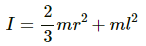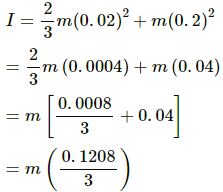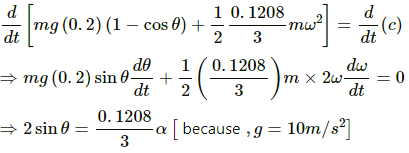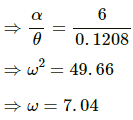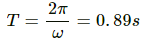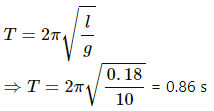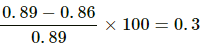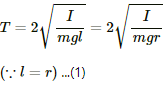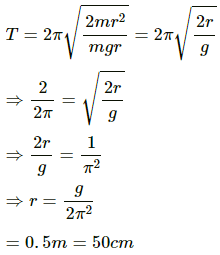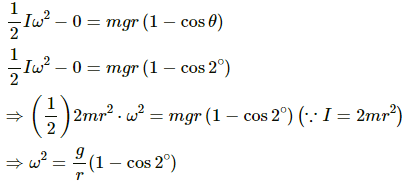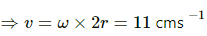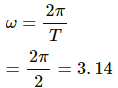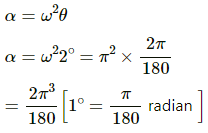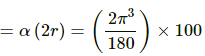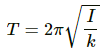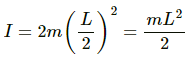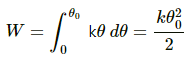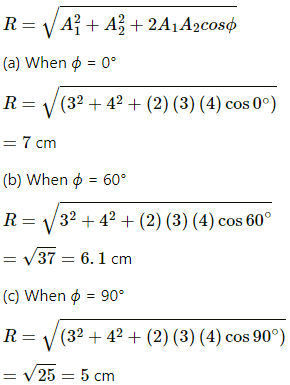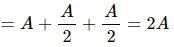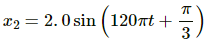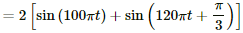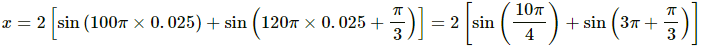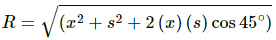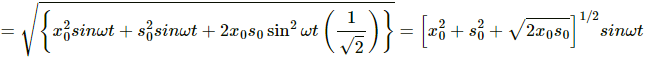HC Verma Questions and Solutions: Chapter 12: Simple Harmonics Motion- 2 | HC Verma Solutions - JEE PDF Download

Q.1. A particle executes simple harmonic motion with an amplitude of 10 cm and time period 6 s. At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.

It is given,
Amplitude of the simple harmonic motion, A =10 cm
At t = 0 and  x = 5 cm,
Time period of the simple harmonic motion, T  = 6 s
Angular frequency (ω) is given by,

Consider the equation of motion of S.H.M,
 Y = Asin(ωt + ∅) ...(1)
where Y is displacement of the particle, and ∅ is phase of the particle.
On substituting the values of A, t and ω in equation (1), we get:
5 = 10sin(ω × 0 + ϕ)
⇒ 5 = 10sin ϕ

∴ Equation of displacement can be written as,

(ii) At t = 4 s,

Acceleration is given by,
a = −ω²x

Q.2. The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitude 2 cm, 1 m s⁻¹ and 10 m s⁻² at a certain instant. Find the amplitude and the time period of the motion.

It is given that:
Position of the particle, x = 2 cm = 0.02 m
Velocity of the particle, v = 1 ms−1.
Acceleration of the particle, a = 10 ms−2.
Let
ω be the angular frequency of the particle.
The acceleration of the particle is given by,
 a = ω²x

Time period of the motion is given as,

Now, the amplitude A is calculated as,

Q.3. A particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?

It is given that:
Amplitude of the particle executing simple harmonic motion, A = 10 cm
To determine the distance from the mean position, where the kinetic energy of the particle is equal to its potential energy:
Let y be displacement of the particle,
ω be the angular speed of the particle, and
A be the amplitude of the simple harmonic motion.
Equating the mathematical expressions for K.E. and P.E. of the particle, we get :

The kinetic energy and potential energy of the particle are equal at a distance of 5√2 cm from the mean position.

Q.4. The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s². Find the position(s) of the particle when the speed is 8 cm/s.

It is given that:
Maximum speed of the particle,
Maximum acceleration of the particle,
a_max = 50 cms⁻²
The maximum velocity of a particle executing simple harmonic motion is given by,
v_Max = Aω
where  omega is angular frequency, and  omega is angular frequency, and A is amplitude of the particle.
Substituting the value of v_Max in the above expression,
we get :
Aω = 10 ...(1)

a_Max = ω²A = 50 cms⁻¹

From the equations (1) and (2), we get:

To determine the positions where the speed of the particle is 8 ms^-1, we may use the following formula:
v² = ω² (A² − y²)
where y is distance of particle from the mean position, and v is velocity of the particle.
On substituting the given values in the above equation, we get:
64 = 25 (4 − y²)

⇒ 4 − y² = 2.56
⇒ y² = 1.44
⇒  y  = √1.44
⇒y = ± 1.2 cm   (from the mean position)

Q.5. A particle having mass 10 g oscillates according to the equation x = (2.0 cm) sin [(100 s⁻¹)t + π/6]. Find (a) the amplitude, the time period and the spring constant. (c) the position, the velocity and the acceleration at t = 0.

Given:
Equation of motion of the particle executing S.H.M ,

 Mass of the particle, m = 10g ...(1)
General equation of the particle is given by,

On comparing the equations (1) and (2) we get:
(a) Amplitude, A is 2 cm.
Angular frequency, ω is 100 s⁻¹.
Time period is calculated as,

Also, we know -

where k is the spring constant.

(b) At t = 0 and x = 2 cm
 from the mean position,
We know:
x = A sin (ωt + ϕ)
Using

(c) Acceleration of the particle is given by,
a = -ω²x
= 100²×1 = 10000 cm/s²

Q.6. The equation of motion of a particle started at t = 0 is given by x = 5 sin (20t + π/3), where x is in centimetre and t in second. When does the particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?

Given:
The equation of motion of a particle executing S.H.M. is,

The general equation of S..H.M. is give by,

(a) Maximum displacement from the mean position is equal to the amplitude of the particle.
As the velocity of the particle is zero at extreme position, it is at rest.
∴ Displacement   x = 5, which is also the amplitude of the particle.

Now,

The particle will come to rest at
(b)  Acceleration is given as,
a = ω²x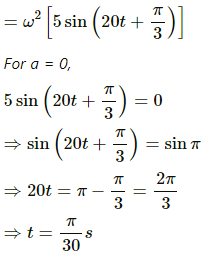
 
(c) The maximum speed (v) is given by,

For maximum velocity: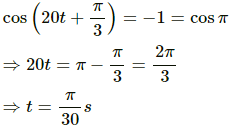
  

Q.7. Consider a particle moving in simple harmonic motion according to the equation x = 2.0 cos (50 πt + tan⁻¹ 0.75) where x is in centimetre and t in second. The motion is started at t = 0. (a) When does the particle come to rest for the first time? (b) When does he acceleration have its maximum magnitude for the first time? (c) When does the particle come to rest for the second time?

It is given that a particle executes S.H.M.
Equation of S.H.M. of the particle:
x = 2.0 cos (50 π t + tan⁻¹0.75)
= 2.0 cos (50 π t + 0.643)
(a) Velocity of the particle is given by,
v = dx/dt v = −100 πsin (50 πt + 0.643)
As the particle comes to rest, its velocity becomes be zero.
⇒ v = −100 πsin (50 πt + 0.643) = 0
⇒ sin (50πt + 0.643) =0 = sinπ
When the particle initially comes to rest,
50πt + 0.643 =π
⇒  t = 1.6 × 10⁻² s
(b) Acceleration is given by,

For maximum acceleration:
cos (50πt + 0.643) = −1 = cosπ(max) (so that a is max)
⇒ t = 1.6 ×  10⁻² s
(c) When the particle comes to rest for the second time, the time is given as,
50πt + 0.643 = 2π
⇒ t = 3.6 × 10⁻² s

Q.8. Consider a simple harmonic motion of time period T. Calculate the time taken for the displacement to change value from half the amplitude to the amplitude.

As per the conditions given in the question,

(for the given two positions)
Let y₁ and y₂ be the displacements at the two positions and A be the amplitude.
Equation of motion for the displacement at the first position is given by, y₁ = Asinωt₁
As displacement is equal to the half of the amplitude,

The displacement at second position is given by,
y₂ = A sin ωt₂
As displacement is equal to the amplitude at this position,
⇒ A = A sin ωt₂
⇒ sinωt₂ = 1

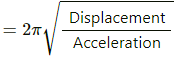
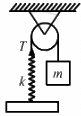
Q.9. The pendulum of a clock is replaced by a spring-mass system with the spring having spring constant 0.1 N/m. What mass should be attached to the spring?

Given:
Spring constant, k =0.1 N/m
Time period of the pendulum of clock, T = 2 s
Mass attached to the string, m, is to be found.
The relation between time period and spring constant is given as,

On substituting the respective values, we get:

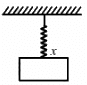
Q.10. A block suspended from a vertical spring is in equilibrium. Show that the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.

An equivalent simple pendulum has same time period as that of the spring mass system.
The time period of a simple pendulum is given by,

where l is the length of the pendulum, and g is acceleration due to gravity.
Time period of the spring is given by,

where m is the mass, and k is the spring constant.
Let x be the extension of the spring.
For small frequency, T_P can be taken as equal to T_S.    

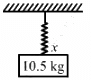
Q.11. A block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314 s. Find the maximum force exerted by the spring on the block.

It is given that:
Amplitude of simple harmonic motion, x = 0.1 m
Time period of simple harmonic motion, T  = 0.314 s
Mass of the block, m = 0.5 kg
Weight of the block, W = mg = 0.5 x 10 = 5 kg
Total force exerted on the block = Weight of the block + spring force

Periodic time of spring is given by,

∴ The force exerted by the spring on the block (F) is,
F = kx = 200.0 × 0.1 = 20 N
Maximum force = F + weight of the block
= 20 + 5 = 25 N

Q.12. A body of mass 2 kg suspended through a vertical spring executes simple harmonic motion of period 4 s. If the oscillations are stopped and the body hangs in equilibrium find the potential energy stored in the spring.

It is given that:
Mass of the body, m = 2 kg
Time period of the spring mass system, T = 4 s
The time period for spring-mass system is given as,

where k is the spring constant.
On substituting the respective values, we get:

As the restoring force is balanced by the weight, we can write:
F = mg = kx

∴ Potential Energy (U) of the spring is,

Q.13. A spring stores 5 J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?

It is given that:
Energy stored in the spring, E = 5 J
Frequency of the mass-spring system, f = 5
Extension in the length of the spring, x = 25 cm = 0.25 m
Time  period, T = (1/5)s
Potential  energy (U) is  given  by,

Time period  of  spring  mass  system  is  given  by,
 where  m  is  the  mass  of the body hanged, and k is  the spring constant .
On  substituting  the  respective  values  in the above expression, we  get:

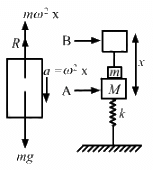
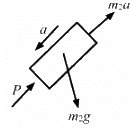
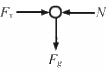
Q.14. A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscillates vertically. (a) Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. (b) Find the normal force on the smaller block at this position. When is this force smallest in magnitude? (c) What can be the maximum amplitude with which the two blocks may oscillate together?

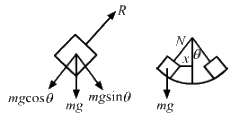
(a) Consider the free body diagram.
Weight of the body, W = mg
Force, F = ma = mω²x
x is the small displacement of mass m.
As normal reaction R is acting vertically in the upward direction, we can write:
R + mω²x − mg = 0  ....(1)
Resultant force = mω²x = mg − R

(b) R = mg − mω²x

It can be seen from the above equations that, for R to be smallest, the value of mω2xshould be maximum which is only possible when the particle is at the highest point.
(c) R = mg − mω²x
As the two blocks oscillate together R becomes greater than zero.
When limiting condition follows,
i.e. R = 0
mg = mω²x

Required maximum amplitude

Q.15. The block of mass m₁ shown in figure is fastened to the spring and the block of mass m₂ is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance (2/k) (m₁ + m₂)g sin θ against the spring and released. Find the position where the two blocks separate. (c) What is the common speed of blocks at the time of separation?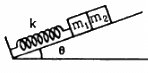

(a) As it can be seen from the figure,
Restoring force = kx
Component of total weight of the two bodies acting vertically downwards = (m₁ + m₂) g sin θ
At equilibrium,  
kx = (m₁ + m₂) g sin θ


(b) It is given that:
Distance at which the spring is pushed,

As the system is released, it executes S.H.M.
where
When the blocks lose contact, P becomes zero. (P is the force exerted by mass m₁ on mass m₂)

Therefore, the blocks lose contact with each other when the spring attains its natural length.

(c) Let v be the common speed attained by both the blocks.
 

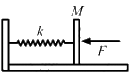
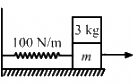
Q.16. In following figure k = 100 N/m M = 1 kg and F = 10 N. (a) Find the compression of the spring in the equilibrium position. (b) A sharp blow by some external agent imparts a speed of 2 m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant. (c) Find the time period of the resulting simple harmonic motion. (d) Find the amplitude. (e) Write the potential energy of the spring when the block is at the left extreme. (f) Write the potential energy of the spring when the block is at the right extreme.
The answer of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy.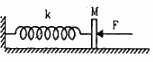

It is given that :
Spring constant, k = 100 N/m,
Mass of the block, M = 1 kg
Force, F = 10 N

(a) In the equilibrium position,
F = kx
where x is the compression of the spring, and k is the spring constant.

(b) The blow imparts a speed of 2 ms^-1 to the block, towards left.
Potential energy of spring, U = 1/2 kx²
Kinetic energy,
K = 1/2 Mv²
(c) Time period (T)  is given by,

(d) Let A be the amplitude.
Amplitude is the distance between the mean and the extreme position.
At the extreme position, compression of the spring will be (A + x).
As the total energy in S.H.M.  remains constant, we can write:

∴ 50(A + 0.1)2 = 2.5 + 10x
⇒ 50A2 + 0.5 + 10A = 2.5 + 10A
⇒ 50A2 = 2

(e) Potential Energy at the left extreme will be,

(f) Potential Energy at the right extreme is calculated as:
Distance between the two extremes = 2A

As the work is done by the external force of 10 N, different values of options (b), (e) and (f) do not violate the law of conservation of energy.

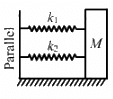
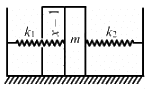
Q.17. Find the time period of the oscillation of mass m in figures  a, b, c. What is the equivalent spring constant of the pair of springs in each case?]

(a) Spring constant of a parallel combination of springs is given as,
K = k1 + k₂  (parallel)
Using the relation of time period for S.H.M. for the given spring-mass system, we have :


(b) Let x be the displacement of the block of mass m, towards left.
Resultant force is calculated as,
F = F₁ + F₂ = (k₁ + k₂)x
Acceleration (a) is given by,

Time period (T) is given by ,

On  substituting  the  values  of  displacement  and  acceleration,   we  get:


Required spring constant, K = k₁ + k₂
(c) Let K be the equivalent spring constant of the series combination.

Time  period  is  given  by

On  substituting  the respective values, we  get:

Q.18. The spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find (a) the amplitude and the time period of the motion of the block, (b) the energy stored in the spring when the block passes through the equilibrium position and (c) the kinetic energy of the block at this position.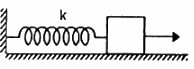

(a) We know-
f = kx
⇒ x = F/k
Acceleration = F/m
Using the relation of time period of S.H.M.,

Amplitude = Maximum displacement = F/k
When the block passes through the equilibrium position, the energy contained by the spring is given by,

(b) At the mean position, potential energy is zero.
Kinetic energy is given by,

Q.19. A particle of mass m is attatched to three springs A, B and C of equal force constants kas shown in figure . If the particle is pushed slightly against the spring C and released, find the time period of oscillation.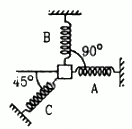

(a) Let us push the particle lightly against the spring C through displacement x.

As a result of this movement, the resultant force on the particle is kx.
The force on the particle due to springs A and B is
Total Resultant force
= kx + kx = 2kx
Acceleration is given by =
Time  period  

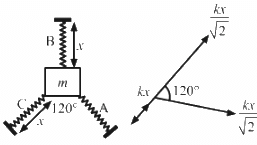
Q.20. Repeat the previous exercise if the angle between each pair of springs is 120° initially.

As the particle is pushed against the spring C by the distance x, it experiences a force of magnitude kx.

If the angle between each pair of the springs is 120˚ then the net force applied by the springs A and B is given as,

Total resultant force (F) acting on mass m will be,

∴ Time  period,

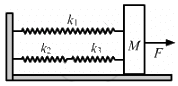
Q.21. The springs shown in the figure are all unstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block. Find the amplitude and the frequency of the motion of the block.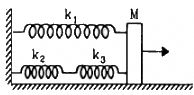

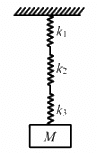
As the block of mass M is pulled, a net resultant force is exerted by the three springs opposing the motion of the block.
Now, springs k₂ and k₃ are in connected as a series combination.
Let k₄ be the equivalent spring constant.

k₄ and k₁ form a parallel combination of springs. Hence, equivalent spring constant k = k₁ + k₄.

(b) Frequency (v) is given by,

(c) Amplitude (x) is given by

Q.22. Find the elastic potential energy stored in each spring shown in figure when the block is in equilibrium. Also find the time period of vertical oscillation of the block.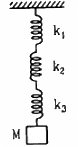

All three spring attached to the mass M are in series.
k₁, k₂, k₃ are the spring constants.
Let k be the resultant spring constant.

Time  period (T) is  given  by,

As force is equal to the weight of the body,
 F = weight = Mg
Let x₁, x₂, and x₃ be the displacements of the springs having spring constants k₁, k₂ and k₃ respectively.
For spring k₁,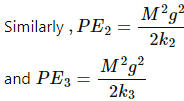

 

Q.23. The string the spring and the pulley shown in figure are light. Find the time period of the mass m.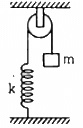

Let l be the extension in the spring when mass m is hung.

Let T₁ be the tension in the string; its value is given by,
T₁ = kl = mg
Let x be the extension in the string on applying a force F.
Then, the new value of tension T₂ is given by,
T₂ = k(x + l)
Driving force is the difference between tensions T₁ and T₂.
∴ Driving force = T₂ − T₁ = k(x + l) − kl
= kx
Acceleration, a =kx/m
Time  period (T) is  given  by,

Q.24. Solve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.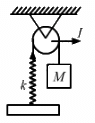

Let us try to solve the problem using energy method.
If δ is the displacement from the mean position then, the initial extension of the spring from the mean position is given by, δ = mg/k
Let x be any position below the equilibrium during oscillation.
Let v be the velocity of mass m and ω be the angular velocity of the pulley.
If r is the radius of the pulley then
v = rω
As total energy remains constant for simple harmonic motion, we can write:

By taking derivatives with respect to t, on both sides, we have:

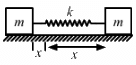
Q.25. Consider the situation shown in figure . Show that if the blocks are displaced slightly in opposite direction and released, they will execute simple harmonic motion. Calculate the time period.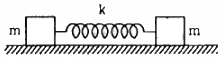

The centre of mass of the system should not change during simple harmonic motion.
Therefore, if the block m on the left hand side moves towards right by distance x, the block on the right hand side should also move towards left by distance x. The total compression of the spring is 2x.
If v is the velocity of the block. Then
Using energy method, we can write:

By taking the derivative of both sides with respect to t, we get:

Q.26. A rectangle plate of sides a and b is suspended from a ceiling by two parallel string of length L each in Figure . The separation between the string is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.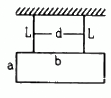

Let m is the mass of rectangular plate and x is the displacement of the rectangular plate.

During the oscillation, the centre of mass does not change.
Driving force (F) is given as,
F = mgsin θ
Comparing the above equation with F = ma, we get:

For small values of θ, sinθ can be taken as equal to θ.
Thus, the above equation reduces to:
  [Where  g  and  L  are  constant.]
It can be seen from the above equation that, a α x.
Hence, the motion is simple harmonic.
Time period of simple harmonic motion (T) is given by,

Q.27. A 1 kg block is executing simple harmonic motion of amplitude 0.1 m on a smooth horizontal surface under the restoring force of a spring of spring constant 100 N/m. A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, find the frequency and the amplitude of the motion.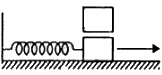

It is given that:
Amplitude of simple harmonic motion, x  = 0.1 m
Total mass of the system, M = 3 + 1 = 4 kg (when both the blocks move together)
Spring constant, k = 100 N/m
Time period of SHM (T) is given by,

\[\text { On  substituting  the  values  of  M  and  k  in  the  bove  equation,   we  have:

Frequency  of  the  motion  is  given  by,
Let v be the velocity of the 1 kg block, at mean position.
As  kinetic  energy  is  equal  to  the  potential  energy,   we  can  write:  
where x = amplitude = 0.1 m
Substituting  the  value  of  x  in  above  equation  and  solving  for  v,   we  get:

When the 3 kg block is gently placed on the 1 kg block, the 4 kg mass and the spring become one system. As a spring-mass system experiences external force, momentum should be conserved.
Let V be the velocity of 4 kg block.
Now,
Initial momentum = Final momentum
∴ 1 × v = 4 × V

Thus, at the mean position, two blocks have a velocity of
Mean  value  of  kinetic  energy  is  given  as,

At the extreme position, the spring-mass system has only potential energy.

where δ is the new amplitude.

Q.28. The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.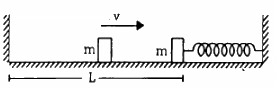

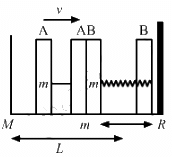
According to the question, the collision is elastic and the surface is frictionless, therefore, when the left block A moves with speed v and collides with the right block B, it transfers all the energy to the right block B.
The left block A moves a distance x against the spring; the right block returns to the original position and completes half of the oscillation.
Therefore, the period of right block B will be,
Right block B collides with left block A and comes to rest.
Let L be the distance moved by the block to return to its original position.
The time taken is given by,

Hence, time period of the periodic motion is,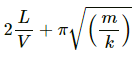
 

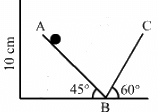
Q.29. Find the time period of the motion of the particle shown in figure. Neglect the small effect of the bend near the bottom.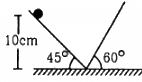

Let t₁ and t₂  be the time taken by the particle to travel distances AB and BC respectively.
Acceleration for part AB, a₁ = g sin 45°
The distance travelled along AB is s₁.

Let v be the velocity at point B, and u be the initial velocity.
Using the third equation of motion, we have:
v² − u² = 2a₁s₁


For the distance BC,
Acceleration, a₂ = −gsin 60°

v = 0

Thus, the total time period, t = 2(t₁ + t₂) = 2 (0.2 + 0.163) = 0.73 s

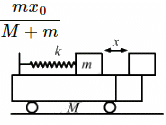
Q.30. All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x₀ when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.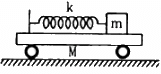

Let x₁ and x₂ be the amplitudes of oscillation of masses m and M respectively.
(a) As the centre of mass should not change during the motion, we can write:
mx₁ = Mx₂ ...(1)
Let k be the spring constant. By conservation of energy, we have:

where x₀ is the length to which spring is stretched.
From equation (2) we have,
x₀ = x₁ + x₂
On substituting the value of x₂ from equation (1) in equation (2), we get:

On substituting the value of x₁ from above equation, we get:    

Thus, the amplitude of the simple harmonic motion of a car, as seen from the road is

(b) At any position,
Let v₁ and v₂ be the velocities.
Using law of conservation of energy we have,

Here, (v₁ − v₂) is the absolute velocity of mass m as seen from the road.
Now, from the principle of conservation of momentum, we have:
Mx₂ = mx₁

Putting the above values in equation (3), we get:

Taking derivative of both the sides, we get: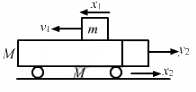

 

Q.31. A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.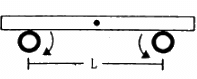

Let x be the displacement of the uniform plate towards left.
Therefore, the centre of gravity will also be displaced through displacement x.
At the displaced position,
R₁ + R₂ = mg
Taking moment about g, we get:


Similarly,

Time  period (T) is  given  by,

Q.32. A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π² m/s².

It is given that:
Time period of the second pendulum, T = 2 s
Acceleration due to gravity of a given place, g = π²ms^-2
The relation between time period and acceleration due to gravity is given by,

where l is the length of the second pendulum.
Substituting the values of T and g, we get:

Hence, the length of the pendulum is 1 m.

Q.33. The angle made by the string of a simple pendulum with the vertical depends on time as 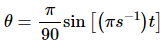.  Find the length of the pendulum if g = π² m².

It  is  given  that:
Angle  made  by  the  simple  pendulum  with  the  vertical,  On  comparing  the  above  equation  with  the  equation  of  S . H . M . , we  get:

Time  period  is  given  by  the  relation,

Hence, length  of  the  pendulum  is  1  m.

Q.34. The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?

Given,
Time period of the clock pendulum = 2.04 s
The number of oscillations made by the pendulum in one day is calculated as

In each oscillation, the clock gets slower by (2.04 − 2.00) s, i.e., 0.04 s.
In one day, it is slowed by = 43200 × (0.04)
= 28.8 min
Thus, the clock runs 28.8 minutes slow during 24 hours.

Q.35. A pendulum clock giving correct time at a place where g = 9.800 m/s² is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.

Let T₁ be the time period of pendulum clock at a place where acceleration due to gravity (g₁) is 9.8 ms⁻².
Let T₁ = 2 s
g₁ =9.8ms^-2
Let T₂ be the time period at the place where the pendulum clock loses 24 seconds during 24 hours.
Acceleration due to gravity at this place is (g₂)

= 9.795m/s²

Q.36. A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillations. (a) How many oscillations does it make per second? (b) What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67 m/s²?

It is given that:
Length of the pendulum, l = 5 m
Acceleration due to gravity, g = 9.8 ms^-2
Acceleration due to gravity at the moon, g' = 1.67 ms^-2
(a) Time period (T)  is given by,

i.e. the body will take  2 π(0.7) seconds to complete an oscillation.
Now, frequency (f) is given by,

(b) Let g' be the value of acceleration due to gravity at moon. Time period of simple pendulum at moon (T′), is given as:

On substituting the respective values in the above formula, we get:

Therefore, frequency (f′) will be,

Q.37. A small block oscillates back and forth on a smooth concave surface of radius R ib Figure . Find the time period of small oscillation.

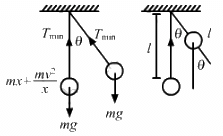
The maximum tension in the string of an oscillating pendulum is double of the minimum tension. Find the angular amplitude.

Let the speed of bob of the pendulum at an angle θ be v.
Using the principle of conservation of energy between the mean and extreme positions, we get:
(1/2)mv² − 0 = mgl(1 − cos θ)
v² = 2gl(1 − cos θ) ...(1)
In a moving pendulum, the tension is maximum at the mean position, whereas it is minimum at the extreme position.
Maximum tension at the mean position is given by
T_max = mg + 2mg(1 − cos θ)
Minimum tension at the extreme position is given by
T_min = m g cosθ
According to the question,
T_max = 2T_min
⇒ mg + 2mg − 2m g cosθ = 2m g cosθ
⇒ 3mg = 4 mg cosθ

Q.38. A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.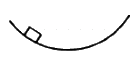

It is given that R is the radius of the concave surface.
Let N be the normal reaction force.
Driving force, F = mg sin θ
Comparing the expression for driving force with the expression, F = ma, we get:
Acceleration, a = g sin θ
Since the value of θ is very small,
∴ sin θ → θ
∴ Acceleration, a = gθ
Let x be the displacement of the body from mean position.

As acceleration is directly proportional to the displacement. Hence, the body will execute S.H.M.
Time period (T) is given by,

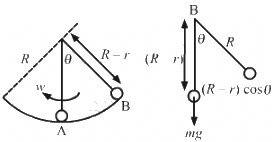
Q.39. A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.

Let ω be the angular velocity of the system about the point of suspension at any time.
Velocity of the ball rolling on a rough concave surface (v_C)  is given by,
 v_c = (R − r)ω
Also, v_c = rω₁
where ω₁ is the rotational velocity of the sphere.


As total energy of a particle in S.H.M. remains constant,

Taking derivative on both sides, we get:


Therefore, the motion is S.H.M.

Time  period  is  given  by,

Q.40. A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.

It is given that:
Length of the pendulum, l = 40 cm = 0.4 m
Radius of the earth, R = 6400 km
Acceleration due to gravity on the earth's surface, g = 9.8 ms^-2
Let
g' be the acceleration due to gravity at a depth of 1600 km from the surface of the earth.
Its value is given by,
  where  d  is  the  depth  from  the  earth  surface, R  is  the  radius  of  earth,  and  g  is  acceleration  due  to  gravity .
On  substituting  the  respective  values,   we  get:

Time period is given as,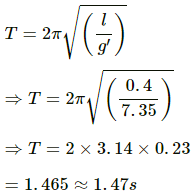
 

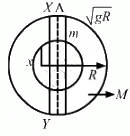
Q.41. Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of 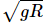 (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of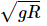

Given:
Radius of the earth is R.
Let M be the total mass of the earth and ρ be the density.
Let mass of the part of earth having radius x be M.

Force on the particle is calculated as,

Now, acceleration (a_x) of mass M' at that position is given by,

So, Time  period  of  oscillation, T =
(a) Velocity-displacement equation in S.H.M is written as,

where, A  is  the  amplitude; and y  is  the  displacement .
When the particle is at y = R,
The velocity of the particle is
On substituting these values in the velocity-displacement equation, we get:

Let t₁ and t₂ be the time taken by the particle to reach the positions X and Y.
Now, phase of the particle at point X will be greater than π/2 but less than π
Also, the phase of the particle on reaching Y will be greater than π but less than 3π/2
Displacement-time relation is given by,
y = A sin ωt
Substituting y = R and A =  in the above relation , we get :

Time taken by the particle to travel from X to Y:

(b) When the body is dropped from a height R
Using the principle of conservation of energy, we get:
Change in P.E. = Gain in K.E.

As the velocity is same as that at X, the body will take the same time to travel XY.
(c) The body is projected vertically upwards from the point X with a velocity  Its velocity becomes zero as it reaches the highest point.
The velocity of the body as it reaches X again will be,

Hence, the body will take same time i.e.
 to travel XY.

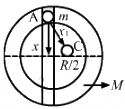
Q.42. Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.

If ρ  is the density of the earth, then mass of the earth (M) is given by,

Similarly, mass (M') of  the  part  of  earth  having  radius (x) is  given  by,

(a) Let F be the gravitational force exerted by the earth on the particle of mass m. Then, its value is given by,

Substituting the value of M' in the above equation, we get:


 (c)


∵ Normal force exerted by the wall N = F_x
(d)The resultant force is
(e) Acceleration = Driving force/mass

Q.43. A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a₀(b) is going down with an acceleration a₀ and (c) is moving with a uniform velocity.

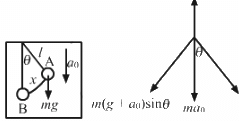
The length of the simple pendulum is l.
Let x be the displacement of the simple pendulum.
(a)

From the diagram, the driving forces f is given by,
f = m(g + a₀)sinθ ...(1)
Acceleration (a) of the elevator is given by,

[ when θ is very small, sin θ → θ = x/l]

As the acceleration is directly proportional to displacement, the pendulum executes S.H.M.
Comparing equation (2) with the expression a = ω²x, we get:

Thus, time period of small oscillations when elevator is going upward(T) will be:


When the elevator moves downwards with acceleration a₀,
Driving force (F) is given by,
 F = m(g − a₀)sinθ
On comparing the above equation with the expression, F = ma, Acceleration,
Time  period  of  elevator  when  it  is  moving  downward (T') is  given  by,

(c) When the elevator moves with uniform velocity, i.e. a₀ = 0,
For a simple pendulum, the driving force (F) is given by,

Comparing  the  above  equation  with  the  expression, F = ma, we  get:

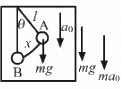
Q.44. A simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π/3 seconds to complete one oscillation. Find the acceleration of the elevator.

It is given that:
Length of the simple pendulum, l = 1  feet
Time period of simple pendulum, T = (π/3)s Acceleration due to gravity, g = 32 ft/s²

Let a be the acceleration of the elevator while moving upwards.
Driving force (f) is given by,
f = m(g + a)sinθ
Comparing the above equation with the expression, f = ma, we get:
Acceleration, a  =  (g + a)sinθ = (g +a)θ (For small angle θ, sin θ → θ)

On substituting the respective values in the above formula, we get:

Q.45. A simple pendulum fixed in a car has a time period of 4 seconds when the car is moving uniformly on a horizontal road. When the accelerator is pressed, the time period changes to 3.99 seconds. Making an approximate analysis, find the acceleration of the car.

It is given that:
When the car is moving uniformly, time period of simple pendulum, T = 4.0 s
As the accelerator is pressed, new time period of the pendulum, T' = 3.99 s
Time period of simple pendulum, when the car is moving uniformly on a horizontal road is given by,

Let the acceleration of the car be a.
The time period of pendulum, when the car is accelerated, is given by:

Taking  the  ratio  of  T  to  T',   we  get:
On solving the above equation for a, we get:

Q.46. A simple pendulum of length l is suspended from the ceiling of a car moving with a speed v on a circular horizontal road of radius r. (a) Find the tension in the string when it is at rest with respect to the car. (b) Find the time period of small oscillation.

It is given that a car is moving with speed v on a circular horizontal road of radius r.
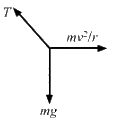
(a) Let T be the tension in the string.

According to the free body diagram, the value of T is given as,

where acceleration,
The time period (T) is given by,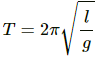
 
On substituting  the respective values, we  have:

Q.47. The ear-ring of a lady shown in figure has a 3 cm long light suspension wire. (a) Find the time period of small oscillations if the lady is standing on the ground. (b) The lady now sits in a merry-go-round moving at 4 m/s¹ in a circle of radius 2 m. Find the time period of small oscillations of the ear-ring.

Given,
Length of the long, light suspension wire, l = 3 cm = 0.03 m
Acceleration due to gravity, g = 9.8 ms^-2
(a)Time Period (T) is given by,

(b) Velocity of merry-go-round, v = 4 ms^-1
Radius of circle, r = 2 m
As the lady sits on the merry-go-round, her earring experiences centripetal acceleration.
Centripetal acceleration (a) is given by,

Resultant acceleration (A) is given by ,

Time Period,

Q.48. Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (c) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.

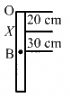
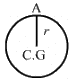
(a) Moment Of inertia (I) about the point X is given by ,

I = I_C.G + mh²

The time Period (T) is given by,
 where I = the  moment  of  inertia,   and  
l = distance  between  the  centre  of  gravity  and  the  point  of  suspension.
On  substituting  the  respective  values  in  the  above  formula, we  get:  = 1.52s
(b) Moment Of inertia (I) about A is given as,
I = I_C.G. + mr² = mr² + mr² = 2mr²

The time period (T) will be,

On  substituting  the  respective  values  in  the  above  equation, we  have:

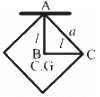
(c) Let I be the moment of inertia of a uniform square plate suspended through a corner.


In the
△ ABC, l² + l² = a²

(d) We  know
h = r/2
Distance  between  the  C . G .   and  suspension  point, l = r/2
Moment of inertia about A will be:
l = I_C.G. + mh²

Time period (T) will be,

Q.49. A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.

It is given that the length of the rod is l.
Let point A be the suspension point and point B be the centre of gravity.
Separation between the point of suspension and the centre of mass, l' = l/2
Also, h = l/2
Using parallel axis theorem, the moment of inertia about A is given as,

Let T' be the time period of simple pendulum of length x.
Time Period (T') is given by
As  the  time  period  of  the  simple  pendulum  is  equal  to  the  time  period  of  the  rod, T' = T

Q.50. A uniform disc of radius r is to be suspended through a small hole made in the disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?

Let m be the mass of the disc and r be its radius.
Consider a point at a distance x from the centre of gravity.
Thus, l = x
Moment of intertia (I) about the point x will be,
I = I_C.G +mx²

Time period(T) is given as,

On  substituting  the  respective  values  in  the  above  equation,   we  get:

To determine the minimum value of T,

On  substituting  the  respective  values  in  the  above  equation,   we  get:

To determine the minimum value of T,

Substituting this value of x in equation (1), we get: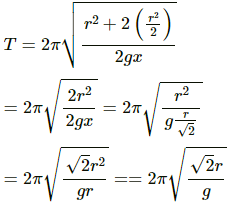
 

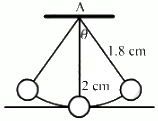
Q.51. A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?

Let I be the moment of inertia and ω be the angular speed.
Using the energy equation, we can write:

Moment  of  inertia  about  the  point  of  suspension  A  is  given  by,

Substituting  the  value  of  l  in  the  above  equation,   we  get:

On substituting the value of I in equation (1) and differentiating it, we get:


Thus,   time  period (T) will  be:

For a simple pendulum, time period (T) is given by,

%   change  in  the  value  of  time  period =
∴ It is about 0.3% greater than the calculated value.

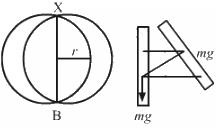
Q.52. A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 2° and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π² m/s².

It is given that:
Time period of oscillation, T = 2 s
Acceleration due to gravity, g = π² ms^-2
Let I be the moment of inertia of the circular wire having mass m and radius r.

(a) Time period of compound pendulum (T) is given by ,

Moment of inertia about the point of suspension  is calculated as,
I = mr² + mr² = 2mr²
On substituting the value of moment of inertia I in equation (1), we get:

(b) From the energy equation, we have:

On  substituing  the  value  of  g  and  r  in  the  above  equation,   we  get: ω = 0.11 rad/s

(c) The acceleration is found to be centripetal at the extreme position.
Centripetal acceleration at the extreme position (a_n)is given by,
a_n = ω²(2r) = (0.11) × 100 = 12 cm/s²
The direction of a_n is towards the point of suspension.
(d) The particle has zero centripetal acceleration at the extreme position. However, the particle will still have acceleration due to the S.H.M.
Angular frequency (ω) is given by,

∴ Angular Accelaration (a) at the extrame position is given as,

Thus , tangential acceleration

= 34 cm/s²

Q.53. A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?

It is given that:
Mass of disc = m
Radius of disc = r
The time period of torsional oscillations is T.
 Moment of inertia of the disc at the centre, I = mr²/2
Time period of torsional pendulum (T) is given by,

where I is the moment of inertia, and k is the torsional constant.
On substituting the value of moment of inertia in the expression for time period T, we have:

On  squaring  both  the  sides,   we  get: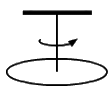

 

Q.54. Two small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ₀ and released. Find the force exerted by the rod on one of the balls as the system passes through the mean position.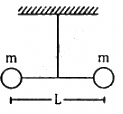

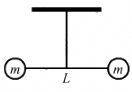
It is given that the mass of both the balls is m and they are connected to each other with the help of a light rod of length L.
Moment of inertia of the two-ball system (I) is given by,


Torque (τ), produced at any given position θ is given as: τ = kθ
⇒ Work done during the displacement of system from 0 to θ₀ will be,

On applying work-energy theorem, we get:


From the free body diagram of the rod, we can write:

Q.55. A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.

It is given that a particle is subjected to two S.H.M.s of same time period in the same direction.
Amplitude of first motion, A₁ = 3 cm
Amplitude of second motion, A₂ = 4 cm
Let ϕ be the phase difference.
The resultant amplitude (R) is given by,

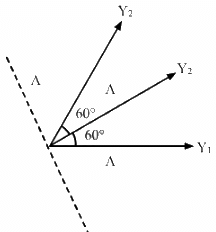
Q.56. Three simple harmonic motions of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 60° ahead of the first and the phase of the third motion is 60° ahead of the second. Find the amplitude of the resultant motion.

It is given that three S.H.M.s of equal amplitudes A and equal time periods are combined in the same direction.
Let Y₁, Y₂ and Y₃ be the three vectors representing the motions, as shown in the figure given below.
According to the question:


By using the vector method, we can find the resultant vector.
Resultant amplitude = Vector sum of the three vectors
= A + A cos 60° + A cos 60°

Q.57. A particle is subjected to two simple harmonic motions given by x₁ = 2.0 sin (100π t) and x₂ = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.

Given are the equations of motion of a particle:
 x₁ = 2.0sin100 πt

The Resultant displacement (x) will be
x = x₁ + x₂

(a) At t = 0.0125 s

(b) At t = 0.025 s

Q.58. A particle is subjected to two simple harmonic motions, one along the X-axis and the other on a line making an angle of 45° with the X-axis. The two motions are given by x = x₀ sin ωt and s = s₀ sin ωt. Find the amplitude of the resultant motion.

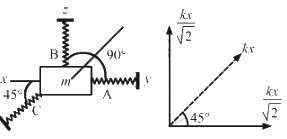
Given:
Equation of motion along X axis, x = x₀ sinωt
Equation of motion along Y axis, s = s₀ sinωt
Angle between the two motions, θ 45°
Resultant motion (R) will be,


Hence, the resultant amplitude is