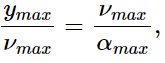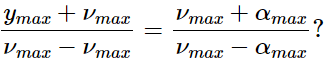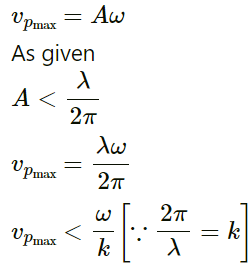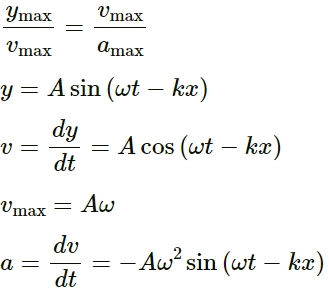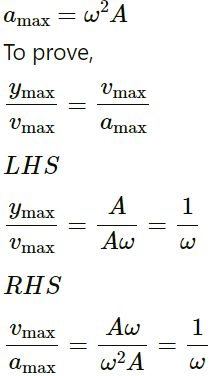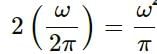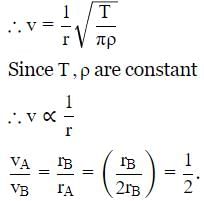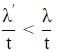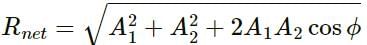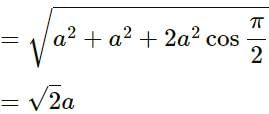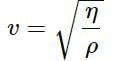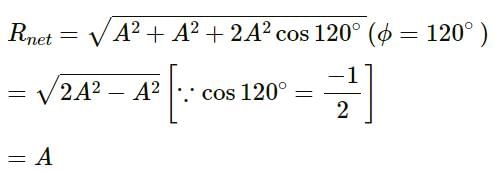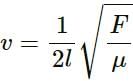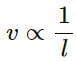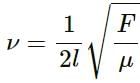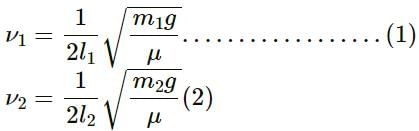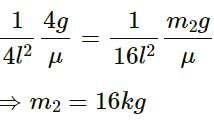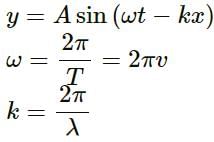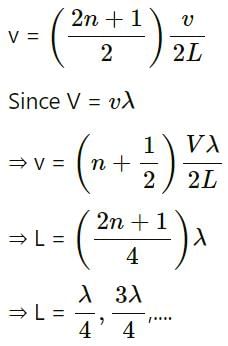Short Answer
Q.1. You are walking along a seashore and a mild wind is blowing. Is the motion of air a wave motion?
No, in wave motion there is no actual transfer of matter but transfer of energy between the points where as when wind blows air particles moves with it.
Q.2. The radio and TV programmes, telecast at the studio, reach our antenna by wave motion. Is it a mechanical wave or nonmechanical?
It is a non-mechanical wave because this type of wave does not require a material medium to travel.
Q.3. A wave is represented by an equation y = c1 sin ( c2x + c3t) In which direction is the wave going? Assume that c1, c2, c3 are all positive.
Equation of the wave is y = c1 sin ( c2x + c3t)
When the variable of the equation is (c2x + c3t), then the wave must be moving in the negative x-axis with time t.
Q.4. Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
Equation of the wave is given by y = Asin(ωt−kx)
where
A is the amplitude
ω is the angular frequency
k is the wave number
Velocity of wave v = ω/k
Velocity of particle, vp = dy/dt = Aw cos(wt - kx)
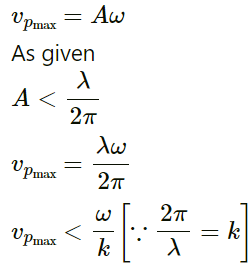
Q.5. Two wave pulses identical in shape but inverted with respect to each other are produced at the two ends of a stretched string. At an instant when the pulses reach the middle, the string becomes completely straight. What happens to the energy of the two pulses?
When two wave pulses identical in shape but inverted with respect to each other meet at any instant, they form a destructive interference. The complete energy of the system at that instant is stored in the form of potential energy within it. After passing each other, both the pulses regain their original shape.
Q.6. Show that for a wave travelling on a string
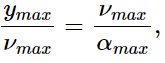
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
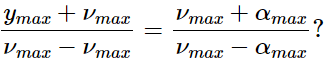
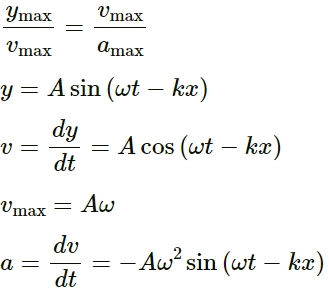
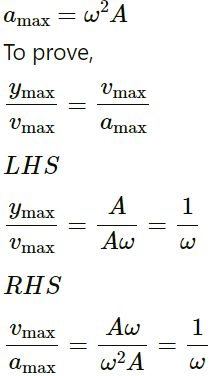
No, componendo and dividendo is not applicable. We cannot add quantities of different dimensions.
Q.7. What is the smallest positive phase constant which is equivalent to 7⋅5 π?
The displacement of a particle on the string is given as
y = A.sin[⍵(t-x/v) + ⲫ]
where ⲫ is the phase constant.
Since a value of the phase constant will be unique for one oscillation and it will be repeated at each 2π angle. So the smallest positive value of ⲫ equivalent to 7.5π will be = 7.5π-2nπ by putting n = 3 i.e., 7.5π-6π
= 1.5π
Q.8. A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone?
Yes, at the centre. The centre position is a node. If the string vibrates in its first overtone, then there will be two positions, i.e., two nodes, one at x = 0 and the other at x = L.
Multiple Choice Questions
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A sine wave is travelling in a medium. The minimum distance between the two particles, always having same speed, is
Explanation
In a sine wave particles that are separated by a distance of odd multiple of half
the wavelength move with same speed and but in opposite direction.
The minimum separation is λ/2.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A sine wave is travelling in a medium. A particular particle has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
Explanation
A sine wave has a maxima and a minima and the particle displacement has phase difference of π radians. Therefore, applying similar argument we can say that if a particular particle has zero displacement at a certain instant, then the particle closest to it having zero displacement is at a distance is equal to λ/2.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Which of the following equations represents a wave traveling along Y-axis?
Explanation
The direction of the displacement of a wave is perpendicular to the wave's motion direction in transverse waves. When a transverse wave is moving in a y-direction, then the displacement of the wave will be in the x-direction, and if the wave which is travelling along the x-axis, its displacement will be towards the y-axis.
The equation for the wave travelling along the y-axis is x = A sin(ky – ωt)
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:The equation y = A sin2 (kx - ωt
represents a wave motion with
Explanation
amplitude A/2, frequency ω/π

Thus, we have:
Amplitude = A/2
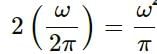
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Which of the following is a mechanical wave?
Explanation
There are mainly two types of waves: first is electromagnetic wave, which does not require any medium to travel, and the second is the mechanical wave, which requires a medium to travel. Sound requires medium to travel, hence it is a mechanical wave.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A cork floating in a calm pond executes simple harmonic motion of frequency v when a wave generated by a boat passes by it. The frequency of the wave is
Explanation
The boat transmits the same wave without any change of frequency to cause the cork to execute SHM with same frequency though amplitude may differ.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed vA and on B with speed vB. The ratio vA/vB is _____.
Explanation
Velocity of a transverse wave in a stretched string

where T is the tension of the string and μ is mass per unit length of the string.
μ = πr2 × ρ
where r is the radius or the string and ρ is the density of the material of the string.
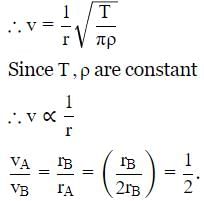
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Both the strings shown in the figure are made of same material and have the same cross-section. The pulleys are light. The wave speed of a transverse wave in the string AB is v1 and in CD it is v2 The v1/v2 is

Explanation
Assuming that the system is in equilibrium, the tension in the string over pulleys is the same in each part say = T. Thus the tension in the string CD = 2T.
So v₁/v₂ = √(F₁µ₂/F₂µ₁), But µ₁ = µ₂
=√(F₁/F₂) = √(T/2T) =1/√2
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Velocity of sound in air is 332 m s−1. Its velocity in vacuum will be
Explanation
Sound wave is a mechanical wave; this means that it needs a medium to travel. Thus, its velocity in vacuum is meaningless.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A wave pulse, travelling on a two-piece string, gets partially reflected and partially transmitted at the junction. The reflected wave is inverted in shape as compared to the incident one. If the incident wave has wavelength λ and the transmitted wave λ'
Explanation
Reflected wave is inverted hence second medium is dir sec with respect to first medium. λ′ <λ
We know that,
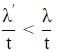
⇒ λ′ < λ
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Two waves represented by y = α sin (ωt - kx) and y = α cos (ωt - kx) y = α cos ωt - kx) are superposed. The resultant wave will have an amplitude
Explanation
We know that the resultant of the amplitude is given by
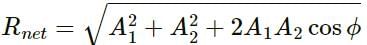
For the particular case, we can write
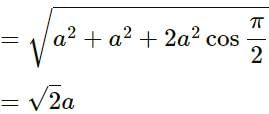
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Two wires A and B, having identical geometrical construction, are stretched from their natural length by small but equal amount. The Young's modulus of the wires are YA and YB whereas the densities are PA and N. It is given that YA > YB and pA > pB transverse signal started at one end takes a time t1 to reach the other end for A and t2 for B.
Explanation
the information is insufficient to find the relation between t1 and t2.
But because the length of wires A and B is not known, the relation between A and B cannot be determined.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Consider two waves passing through the same string. Principle of superposition for displacement says that the net displacement of a particle on the string is sum of the displacements produced by the two waves individually. Suppose we state similar principles for the net velocity of the particle and the net kinetic energy of the particle. Such a principle will be valid for
Explanation
The principle of superposition is valid only for vector quantities. Velocity is a vector quantity, but kinetic energy is a scalar quantity.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
Explanation
The pulses continue to retain their identity after they meet, but the moment they meet their wave profile differs from the individual pulse.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Two periodic waves of amplitudes A1 and A2 pass thorough a region. If A1 > A2, the difference in the maximum and minimum resultant amplitude possible is
Explanation
The maximum amplitude will be obtained when both waves will be in phase, which is (A1 +A2).
Similarly minimum amplitude will be the result of opposite phase,
which is (A1- A2).
Thus the difference will be (A1 +A2) - ( A1 - A2)
which is 2A2
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Two waves of equal amplitude A, and equal frequency travel in the same direction in a medium. The amplitude of the resultant wave is
Explanation
The amplitude of the resultant wave depends on the way two waves superimpose, i.e., the phase angle (φ). So, the resultant amplitude lies between the maximum resultant amplitude (Amax) and the minimum resultant amplitude (Amin).
Amax = A + A = 2A
Amin = A − A = 0
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Two sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120°. The resultant amplitude will be
Explanation
We know the resultant amplitude is given by
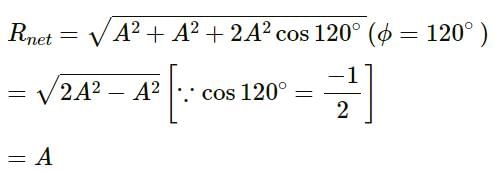
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:The fundamental frequency of a string is proportional to
Explanation
The relation between wave speed and the length of the string is given by
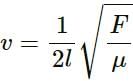
where
- l is the length of the string
- F is the tension
- μ linear mass density
From the above relation, we can say that the fundamental frequency of a string is proportional to the inverse of the length of the string.
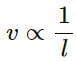
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A tuning fork of frequency 480 Hz is used to vibrate a sonometer wire having natural frequency 240 Hz. The wire will vibrate with a frequency of
Explanation
The frequency of vibration of a sonometer wire is the same as that of a fork. If this happens to be natural frequency of the wire, then standing waves with large amplitude are set up in it.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A tuning fork of frequency 480 Hz is used to vibrate a sonometer wire having natural frequency 410 Hz. The wire will vibrate with a frequency
Explanation
The frequency of vibration of a sonometer wire is the same as that of a fork. If this happens to be the natural frequency of the wire, standing waves with large amplitude are set in it.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A sonometer wire of length l vibrates in fundamental mode when excited by a tuning fork of frequency 416. Hz. If the length is doubled keeping other things same, the string will
Explanation
When the length is doubled keeping other things constant, the fundamental frequency must be halved asf α 1/L But the tuning fork is still vibrating with 416 Hz, which will be the second harmonic of the string. String will vibrate with this frequency only.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A sonometer wire supports a 4 kg load and vibrates in fundamental mode with a tuning fork of frequency 416. Hz. The length of the wire between the bridges is now doubled. In order to maintain fundamental mode, the load should be changed to
Explanation
According to the relation of the fundamental frequency of a string
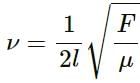
where l is the length of the string
- F is the tension
- μ is the linear mass density of the string
We know that ν1 = 416 Hz, l1 = l and l2 = 2l.
Also, m1 = 4 kg and m2 = ?
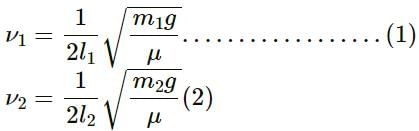
So, in order to maintain the same fundamental mode
v1 = v2
squaring both sides of equations (1) and (2) and then equating
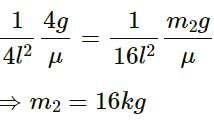
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A mechanical wave propagates in a medium along the X-axis. The particles of the medium
Explanation
A mechanical wave is of two types: longitudinal and transverse. So, a particle of a mechanical wave may move perpendicular or along the direction of motion of the wave.
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A transverse wave travels along the Z-axis. The particles of the medium must move
Explanation
In a transverse wave, particles move perpendicular to the direction of motion of the wave. In other words, if a wave moves along the Z-axis, the particles will move in the X–Y plane.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Longitudinal waves cannot
Explanation
A longitudinal wave has particle displacement along its direction of motion; thus, it cannot be polarised.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A wave going in a solid
Explanation
Particles in a solid are very close to each other; thus, both longitudinal and transverse waves can travel through it.
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A wave moving in a gas
Explanation
Because particles in a gas are far apart, only longitudinal wave can travel through it.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Two particles A and B have a phase difference of π when a sine wave passes through the region.
Explanation
The frequencies of the particles will be the same, so the option (a) is not true.
Let the displacement of the particle at A be y = A' sin(⍵t-kx) and of the particle at B be y' = A' sin(⍵t-kx+π) = -A' sin(⍵t-kx)
So, y = -y'.
Thus A and B move in opposite directions and the displacements at A and B have equal magnitudes.
So, the options (b) and (d) are true.
When the phase difference of A and B is π, the separation between them maybe (nλ+λ/2) = (2n+1)λ/2, where n = 1, 2, 3,....... The option (c) is a special case, hence not true.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A wave is represented by the equation
y = (0 cdot 001 mm) sin [(50s-1)t + (2.0m-1)x]
Explanation
y = (0. 001mm) sin [50s-1) t + (2. om-1)x]
Comparing with the standard equation,
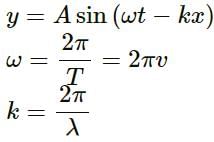
Here, A is the amplitude, ω is the angular frequency, k is the wave number and λ is the wavelength.
A = 0. 001mm
Now,
50 = 2πv
⇒ v = 25/π Hz
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:A standing wave is produced on a string clamped at one end and free at the other. The length of the string ______.
Explanation
The frequency (v) of a standing wave, fixed at one end and free at the other end is:
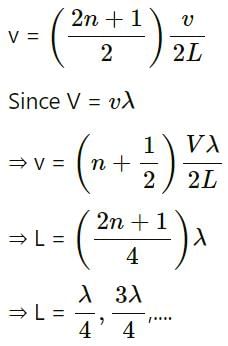
Therefore the length of the string is an odd integral multiple of λ/4
Report a problem
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:Mark out the correct options.
Explanation
A standing wave is formed when the energy of any small part of a string remains constant. If it does not, then there is transfer of energy. In that case, the wave is not stationary.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 1
Try yourself:In a stationary wave,
Explanation
In a stationary wave, all the particles between consecutive nodes vibrate in phase. Option (d) is correct. The particles on the different sides of a node do not vibrate in phase but they have a phase difference of π. So the alternate parts between the consecutive nodes vibrate in phase. Thus the options (a) and (b) are not true but (c) is true.