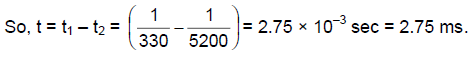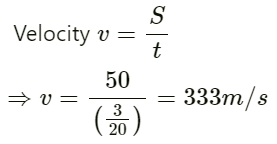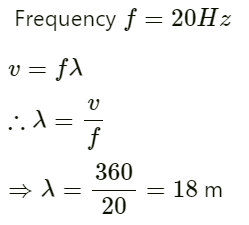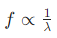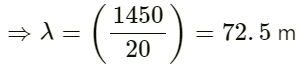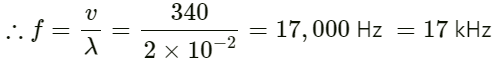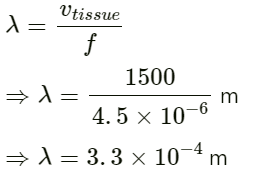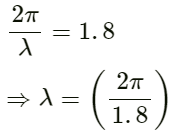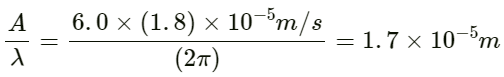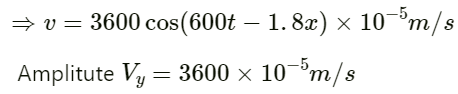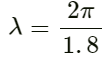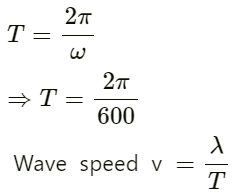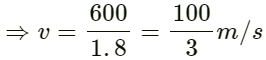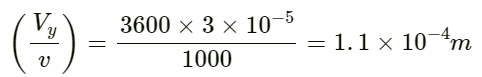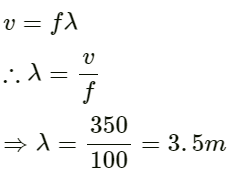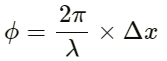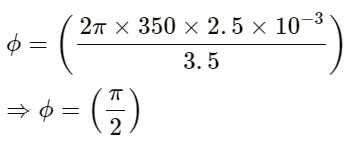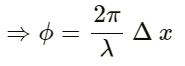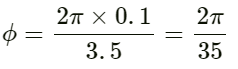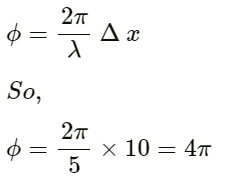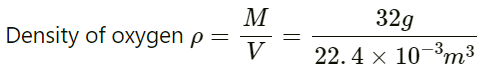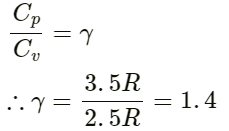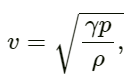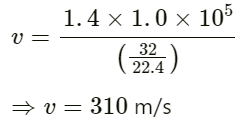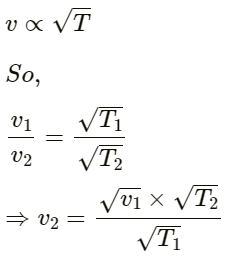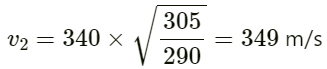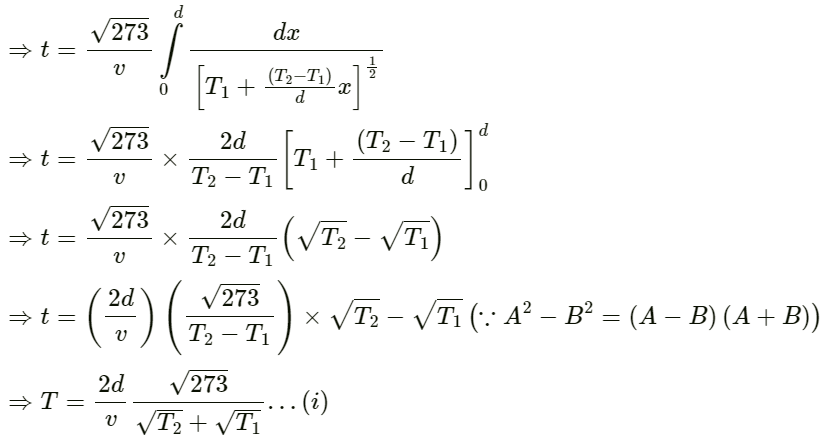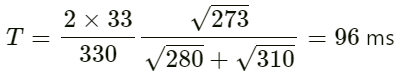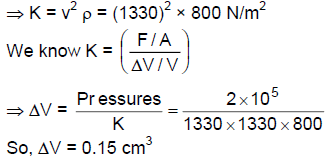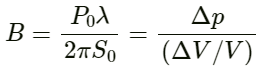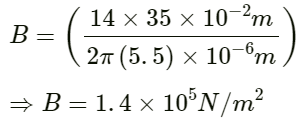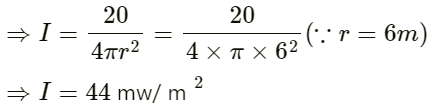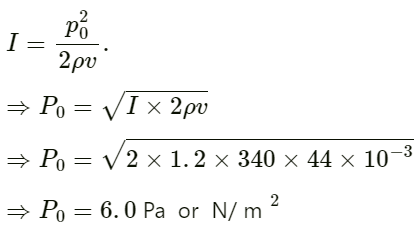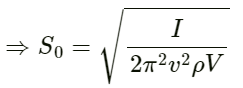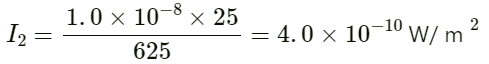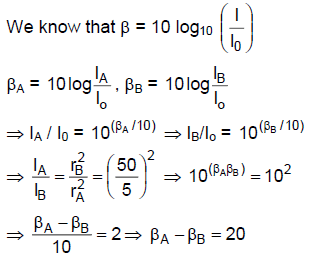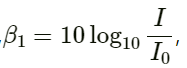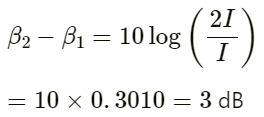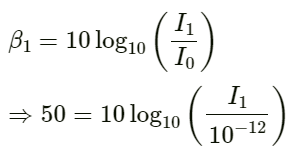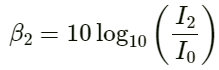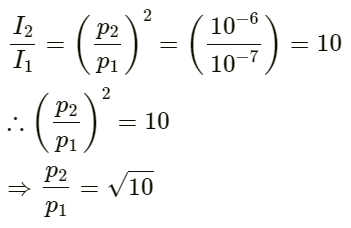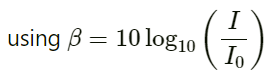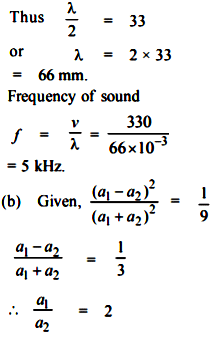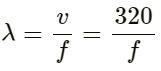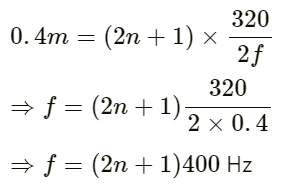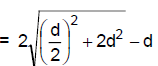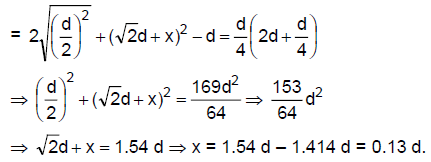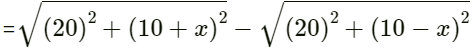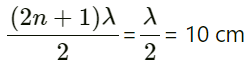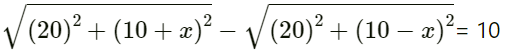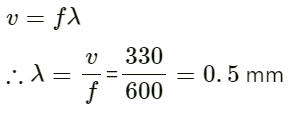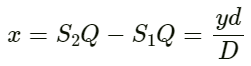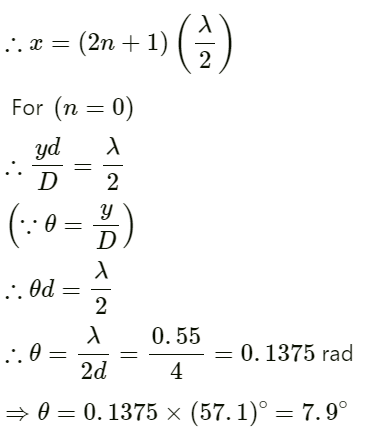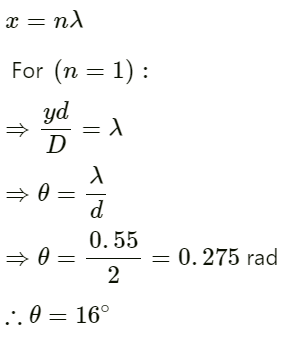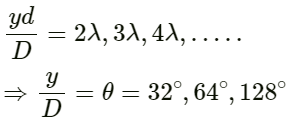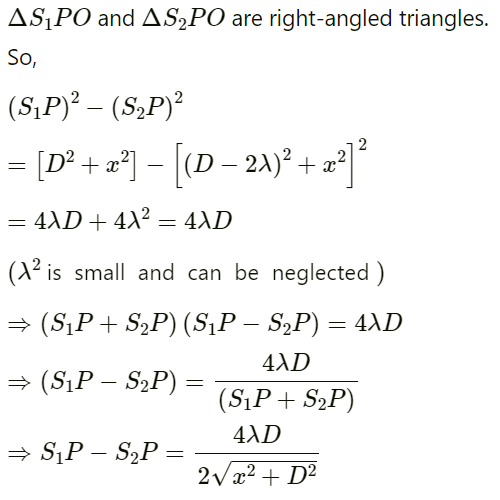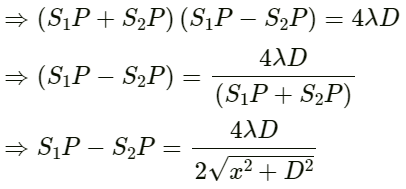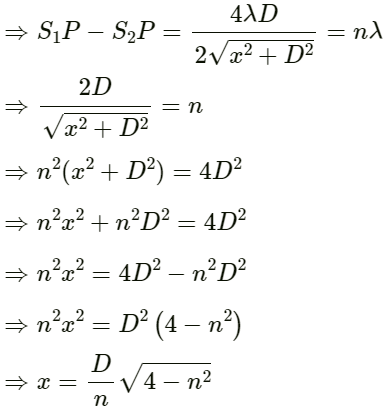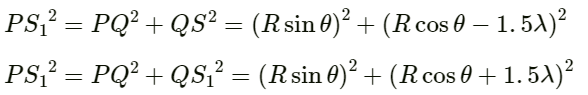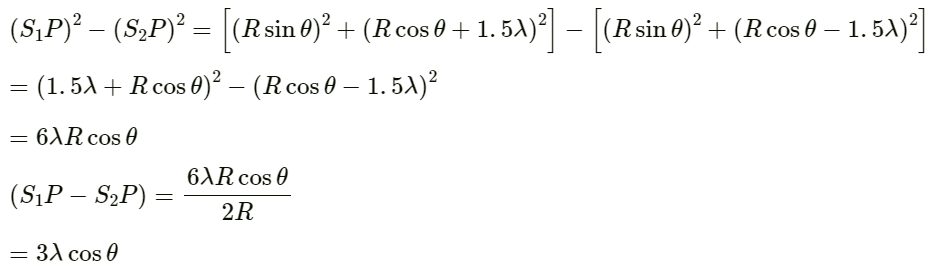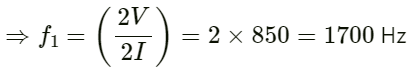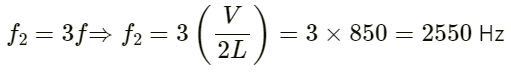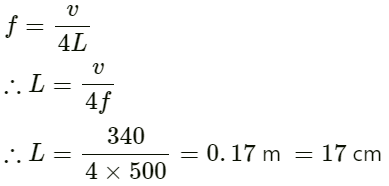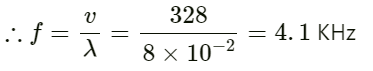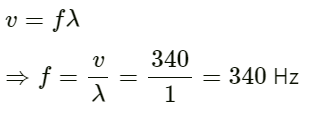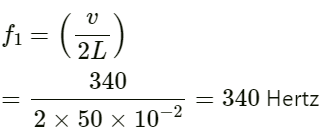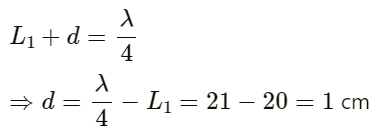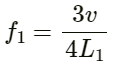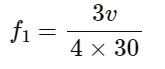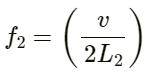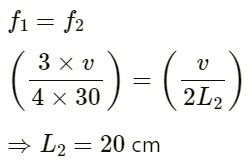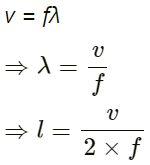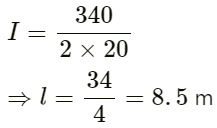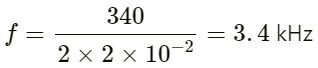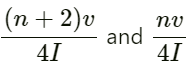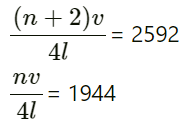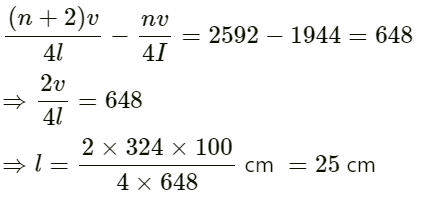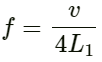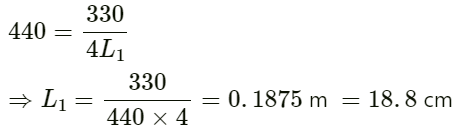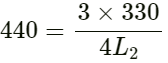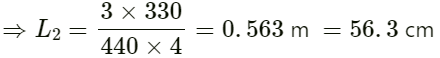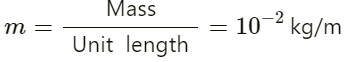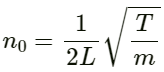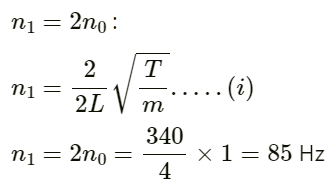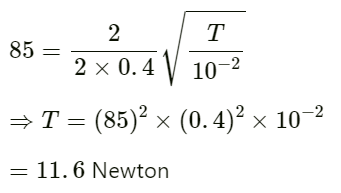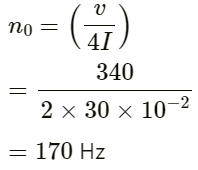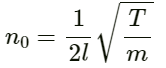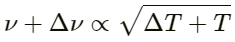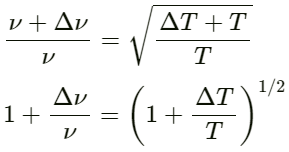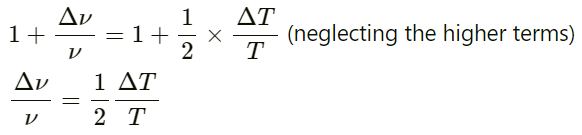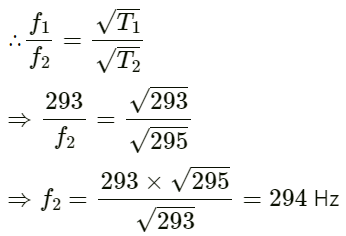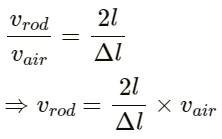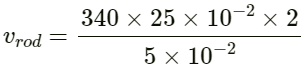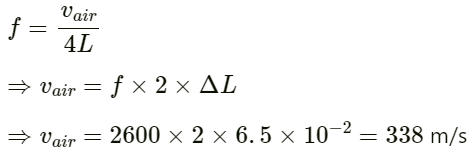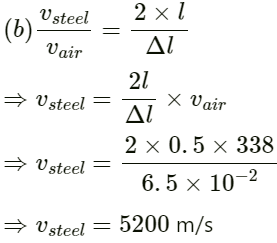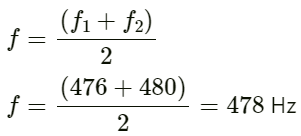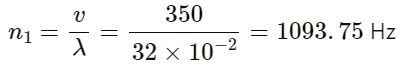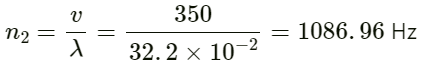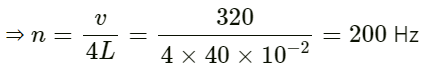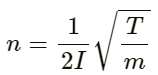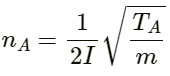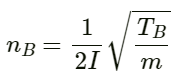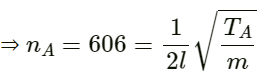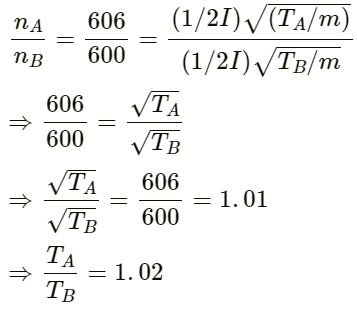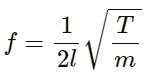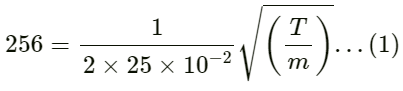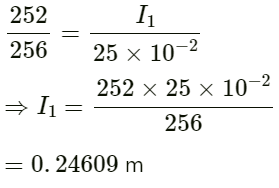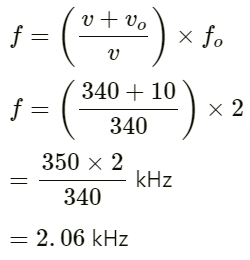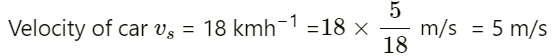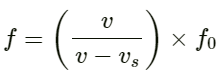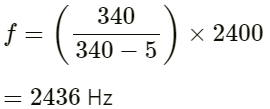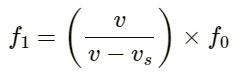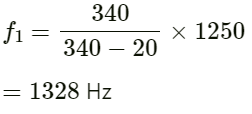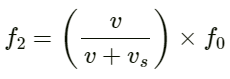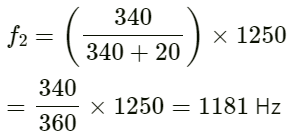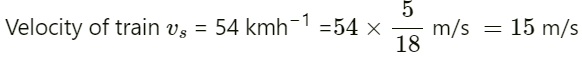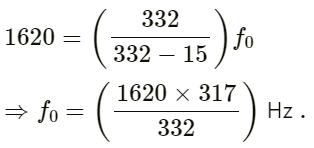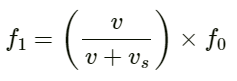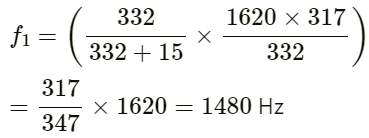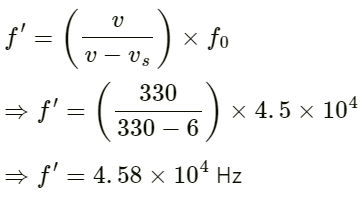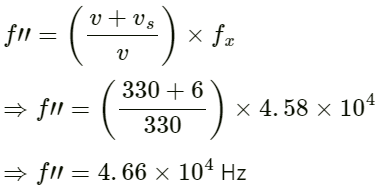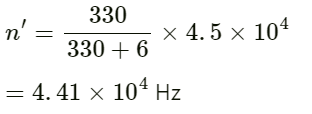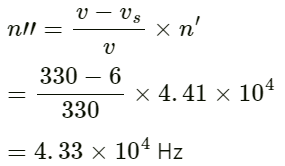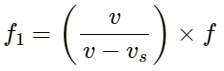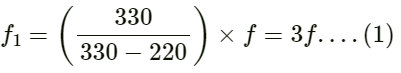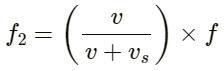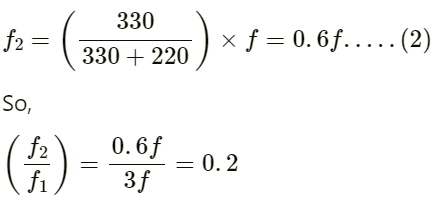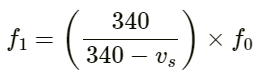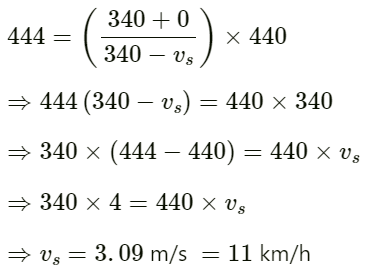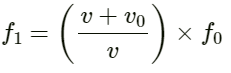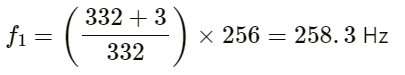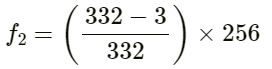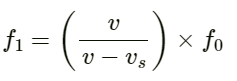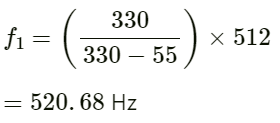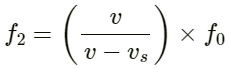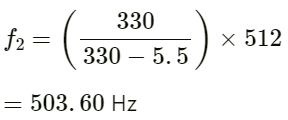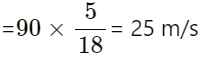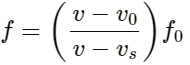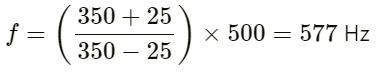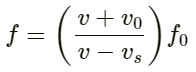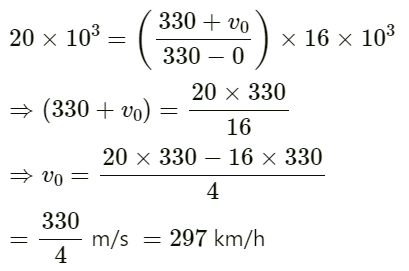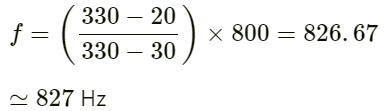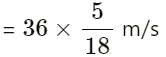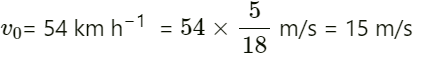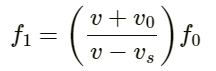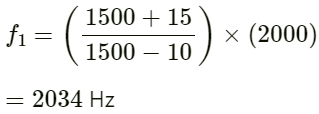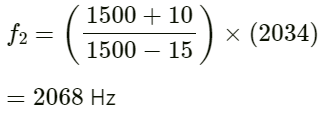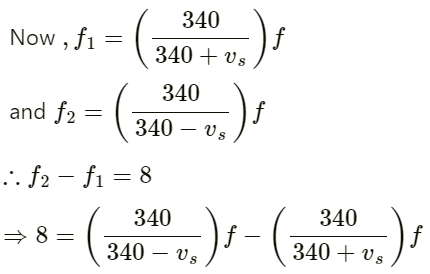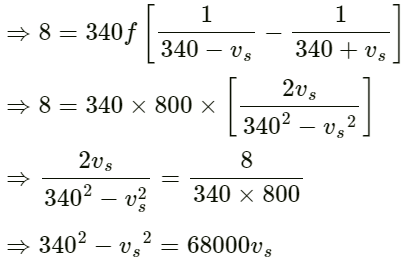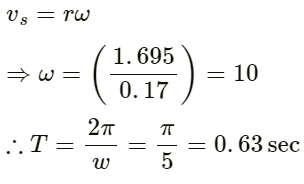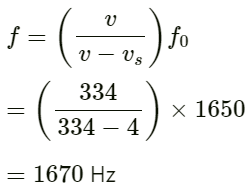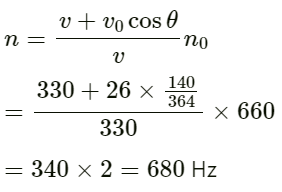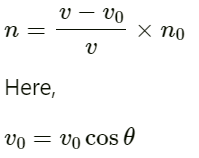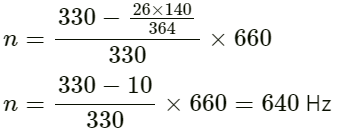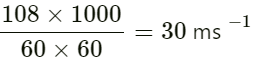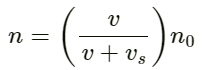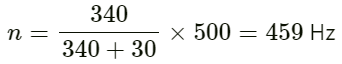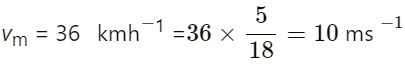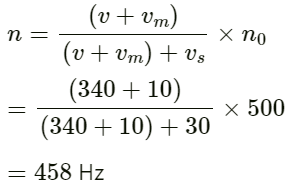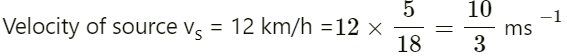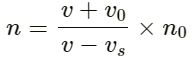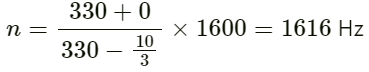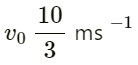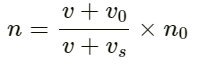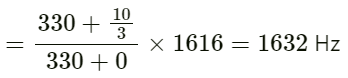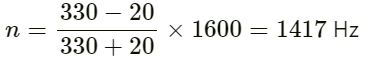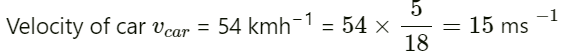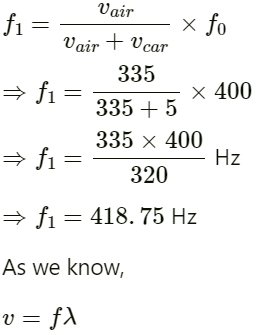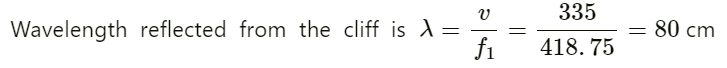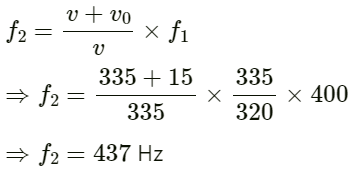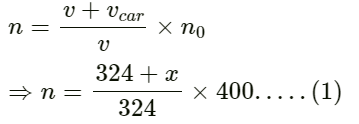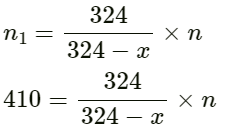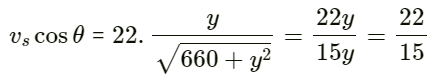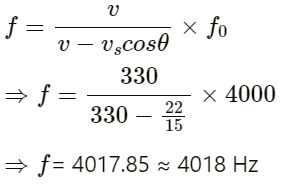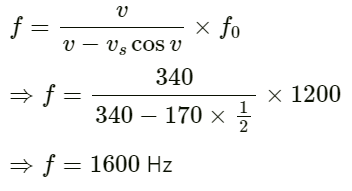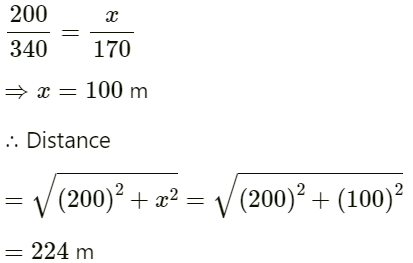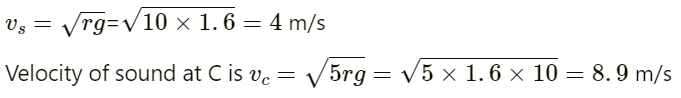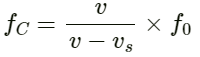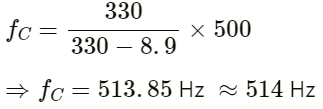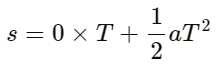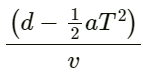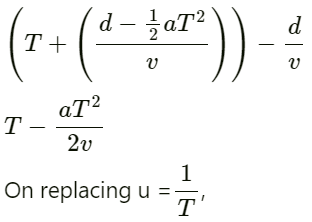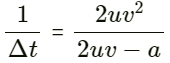HC Verma Questions and Solutions: Chapter 16: Sound Waves- 2 | HC Verma Solutions - JEE PDF Download
Exercise
Q.1. A steel tube of length 1.00 m is struck at one end. A person with his ear close to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
Vair = 230 m/s. Vs = 5200 m/s. Here S = 7 m
Q.2. At a prayer meeting, the disciples sing JAI-RAM JAI-RAM. The sound amplified by a loudspeaker comes back after reflection from a building at a distance of 80 m from the meeting. What maximum time interval can be kept between one JAI-RAM and the next JAI-RAM so that the echo does not disturb a listener sitting in the meeting. Speed of sound in air is 320 m s−1.
Given:
The distance of the building from the meeting is 80 m.
Velocity of sound in air v = 320 ms−1
Total distance travelled by the sound after echo is S = 80 × 2 = 160 m
As we know,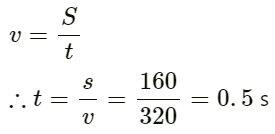
Therefore, the maximum time interval will be 0.5 seconds.
Q.3. A man stands before a large wall at a distance of 50.0 m and claps his hands at regular intervals. Initially, the interval is large. He gradually reduces the interval and fixes it at a value when the echo of a clap merges every 3 seconds, find the velocity of sound in air.
Given:
Distance of the large wall from the man S = 50 m
He has to clap 10 times in 3 seconds.
So, time interval between two claps will be = 3/10 seconds
Therefore, the time taken (t) by sound to go the wall is t = 3/10 seconds
We know that:
Hence, the velocity of sound in air is 333 m/s.
Q.4. A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
Given:
Speed of sound v = 360 ms−1
Therefore, for minimum wavelength, the frequency f = 20 kHz.
We know that v = fλ.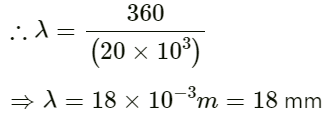
(b) For maximum wave length:
Q.5. Find the minimum and maximum wavelengths of sound in water that is in the audible range (20−20000 Hz) for an average human ear. Speed of sound in water = 1450 m s−1.
Speed of sound in water v = 1450 ms −1
Audible range for average human ear = (20-20000 Hz)
Relation between frequency (f) and wavelength (λ) with constant velocity:
(a) For minimum wavelength, the frequency should be maximum.
Frequency f = 20 kHz
As v = fλ,
(b) For maximum wave length, the frequency should be minimum.
f = 20Hz
v = fλ
∴ λ = 72.5 m
Q.6. Sound waves from a loudspeaker spread nearly uniformly in all directions if the wavelength of the sound is much larger than the diameter of the loudspeaker.
(a) Calculate the frequency for which the wavelength of sound in air is ten times the diameter of the speaker if the diameter is 20 cm.
(b) Sound is essentially transmitted in the forward direction if the wavelength is much shorter than the diameter of the speaker. Calculate the frequency at which the wavelength of the sound is one tenth of the diameter of the speaker described above. Take the speed of sound to be 340 m/s.
Given:
The diameter of the loudspeaker is 20 cm.Velocity of sound in air v = 340 m/s
As per the question,
wavelength (λ) of the sound is 10 times the diameter of the loudspeaker.
∴ (λ) = 20 cm × 10 = 200 cm = 2 m
(a) Frequency f = ?
As we know, v = fλ
(b) Here, wavelength is one tenth of the diameter of the loudspeaker.⇒ λ = 2 cm = 2 × 10−2 m
Q.7. Ultrasonic waves of frequency 4.5 MHz are used to detect tumour in soft tissue. The speed of sound in tissue is 1.5 km s−1 and that in air is 340 m s−1. Find the wavelength of this ultrasonic wave in air and in tissue.
(a) Given:
Frequency of ultrasonic wave f = 4.5 MHz = 4.5 × 106 Hz
Velocity of air v = 340 m/s
Speed of sound in tissue = 1.5 km/s
Wavelength λ = ?
As we know, v = fλ
(b) Velocity of sound in tissue vtissue= 1500 m/s
Q.8. The equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x) where y is measured in 10−5 m, t in second and x in metre.
(a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave.
(b) Find the ratio of the velocity amplitude of the particles to the wave speed.
Given:
Equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x),
where y is measured in 10−5 m,
t in second,
x in metre.
Comparing the given equation with the wave equation, we find:
Amplitude A = 6 × 10-5 m
We have:
So, required ratio:
(b) Let Vy be the velocity amplitude of the wave.
Wavelength:
Time period:
Required ratio:
Q.9. A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1.
(a) By how much is the phase changed at a given point in 2.5 ms?
(b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
Given:
Speed of sound in air v = 350 m/s
Frequency of sound wave f = 100 Hz
a) As we know,
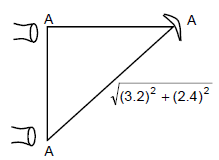
Distance travelled by the particle:
Δx = (350 × 2.5 × 10−3) m
Phase difference is given by:
On substituting the values we get:
(b) For the second case:
Distance between the two points:
∆x = 10 cm = 0.1 m
On substituting the respective values in the above equation, we get:
The phase difference between the two points is 2π/35
Q.10. Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source
(a) on the line joining the sources and
(b) on the perpendicular bisector of the line joining the sources?
Given:
Separation between the two point sources ∆x = 10 cm
Wavelength λ = 5.0 cm
(a) Phase difference is given by:
Therefore, the phase difference is zero.
(b) Zero: the particles are in the same phase since they have the same path.
Q.11. Calculate the speed of sound in oxygen from the following data. The mass of 22.4 litre of oxygen at STP (T = 273 K and p = 1.0 × 105 N m−2) is 32 g, the molar heat capacity of oxygen at constant volume is Cv = 2.5 R and that at constant pressure is Cp = 3.5 R.
Given:
Pressure of oxygen p = 1.0 × 105 Nm−2
Temperature T = 273 K
Mass of oxygen M = 32 g
Volume of oxygen V = 22.4 litre = 22.4 × 10−3m3
Molar heat capacity of oxygen at constant volume Cv = 2.5 R
Molar heat capacity of oxygen at constant pressure Cp = 3.5 R
We know that:
Velocity of sound is given by:where v is the speed of sound. On substituting the respective values in the above formula, we get:
Therefore, the speed of sound in oxygen is 310 m/s.
Q.12. The speed of sound as measured by a student in the laboratory on a winter day is 340 m s−1 when the room temperature is C17°. What speed will be measured by another student repeating the experiment on a day when the room temperature is 32°C?
Given:
Velocity of sound v1 = 340 m/s
Temperature T1 = 17°C = 17 + 273 = 290 K
Let the velocity of sound at a temperature T2 be v2.
T2 = 32°C = 273 + 32 = 305 K
Relation between velocity and temperature:
On substituting the respective values, we get:
Hence, the final velocity of sound is 349 m/s.
Q.13. At what temperature will the speed of sound be double of its value at 0°C?
Let the speed of sound T1 be v1,
where T1 = 0˚ C = 273 K.
Let T2 be the temperature at which the speed of sound (v2) will be double its value at 0˚ C.
As per the question,
v2 = 2v1.
To convert Kelvin into degree celsius:
T2 = (273 × 4) − 273 = 819∘C
Hence, the temperature (T2 ) will be 819˚ C
Q.14. The absolute temperature of air in a region linearly increases from T1 to T2 in a space of width d. Find the time taken by a sound wave to go through the region in terms of T1, T2, d and the speed v of sound at 273 K. Evaluate this time for T1 = 280 K, T2 = 310 K, d = 33 m and v = 330 m s−1.
Given:
The absolute temperature of air in a region increases linearly from T1 to T2 in a space of width d.
The speed of sound at 273 K is v.
vT is the velocity of the sound at temperature T.
Let us find the temperature variation at a distance x in the region.
Temperature variation is given by: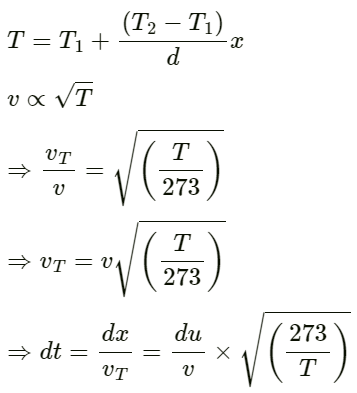
Evaluating this time:
Initial temperature T1 = 280 K
Final temperature T2 = 310 K
Space width d = 33 m
v = 330 m s−1
On substituting the respective values in the above equation, we get:
Q.15. Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0 × 105 N m−2 from the following data. Density of kerosene = 800 kg m−3 and speed of sound in kerosene = 1330 ms−1.
Where K = bulk modulus of elasticity
Q.16. Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
Given:
Wavelength of sound wave
λ = 35 cm = 35 × 10−2m
Pressure amplitude P0 = 1.0 × 105 ± 14Pa
Displacement amplitude of the air particles S0 = 5.5 × 10−6 m
Bulk modulus is given by:
On substituting the respective values in the above equation, we get:
Hence, the bulk modulus of air is 1.4 × 105 N/m2.
Q.17. A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3.
(a) What is the intensity at a distance of 6.0 m from the source?
(b) What will be the pressure amplitude at this point?
(c) What will be the displacement amplitude at this point?
Given:
Velocity of sound in air v = 340 ms−1
Power of the source P = 20 W
Frequency of the source f = 2,000 Hz
Density of air ρ = 1.2 kgm −3
(a) Distance of the source r = 6.0 m
Intensity is given by:
I = P/A
where A is the area.
(b) As we know,
(c) As we know, I = 2π2S02v2ρV.
S0 is the displacement amplitude.
On applying the respective values, we get:
S0 = 1.2 × 10−6 m
Q.18. The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
Given:
The intensity I1 is 1.0 × 10−8 Wm−2,
when the distance of the point source r1 is 5 m.
Let I2 be the intensity of the point source at a distance r2 = 25 m.
As we know,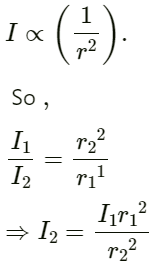
On substituting the respective values, we get:
Q.19. The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
=> βB = 40 – 20 = 20 dβ.
Q.20. If the intensity of sound is doubled, by how many decibels does the sound level increase?
Let the intensity of the sound be I and β1 be the sound level. If the intensity of the sound is doubled, then its sound level becomes 2I.
Sound level β1 is given by,
where I0 is the constant reference intensity.
When the intensity doubles, the sound level is given by: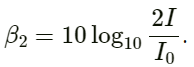
According to the question,
The sound level is increased by 3 dB.
Q.21. Sound with intensity larger than 120 dB appears pain full to a person. A small speaker delivers 2.0 W of audio output. How close can the person get to the speaker without hurting his ears?
Given:
The sound level that can hurt the human ear is 120 dB. Then, the intensity I is 1 W/m2.
Audio output of the small speaker P = 2 W
Let the closest distance be x.
We have:
Hence, the closest distance of the human ear from the small speaker is 40 cm.
Q.22. If the sound level in a room is increased from 50 dB to 60 dB, by what factor is the pressure amplitude increased?
Given:
Initial sound level β1 = 50 dB
Final sound level β2 = 60 dB
Constant reference intensity I0 = 10 −12 W/m2
We can find initial I1 using:
On Solving , We get:
I1 = 10−7W/m2.
Similarly,
On substituting the values and solving, we get:
I2 = 10−6 W/ m 2
As the intensity is proportional to the square of pressure amplitude (p), we have:
Hence, the pressure amplitude is increased by √10 factor.
Q.23. The noise level in a classroom in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student output same sound energy per second, what will be the noise level if the number of students is increased to 100?
Let the intensity of each student be I and the sound level of 50 students be β1.
if the number of students increases to 100, the sound level becomes β2.
where I0 is the constant reference intensity, I is the intensity and β is the sound level.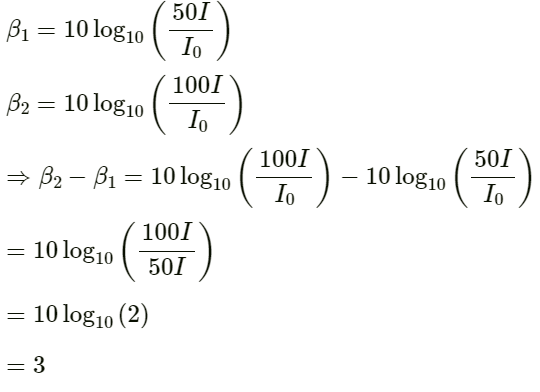
Therefore, the noise level of 100 students
(β2) will be = 53 + 3 = 53dB.
Q.24. In Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340 m s−1.
Distance between tow maximum to a minimum is given by, λ/4 = 2.50cm
Q.25. In Quincke's experiment, the sound intensity has a minimum value l at a particular position. As the sliding tube is pulled out by a distance of 16.5 mm, the intensity increases to a maximum of 9 l. Take the speed of sound in air to be 330 m s−1.
(a) Find the frequency of the sound source.
(b) Find the ratio of the amplitudes of the two waves arriving at the detector assuming that it does not change much between the positions of minimum intensity and maximum intensity.
(a) The distance between minimum to next maximum
= 2 × 16.5 = 33 mm.
This distance must be equal to λ/2.
Q.26. Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air = 320 m s−1.
Given:
Speed of sound in air v = 320 ms−1
The path difference of the sound waves coming from the loudspeaker and reaching the person is given by:
Δx = 6.4 m − 6.0 m = 0.4 m
If (f) is the frequency of either wave, then the wavelength of either wave will be:
For destructive interference, the path difference of the two sound waves reaching the listener should be an odd integral multiple of half of the wavelength.
On substituting the respective values, we get:
Thus, on applying the different values of n, we find that the frequencies within the specified range that caused destructive interference are 1200 Hz, 2000 Hz, 2800 Hz, 3600 Hz and 4400 Hz.
Q.27. A source of sound S and detector D are placed at some distance from one another. a big cardboard is placed near hte detector and perpendicular to the line SD as shown in figure. It is gradually moved away and it is found that the intensity changes from a maximum to a minimum as the board is moved through a distance of 20 cm. Find the frequency of the sound emitted. Velocity of sound in air is 336 m s−1.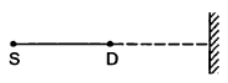
Given:
Velocity of sound in air v = 336 ms−1
Distance between maximum and minimum intensity:
λ/4 = 20
Frequency of sound f = ?
We have:
λ/4 = 20
⇒ λ = 20 × 4 = 80 cm = 80 × 10−2 m
As we know,
Therefore, the frequency of the sound emitted from the source is 420 Hz.
Q.28. A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what
minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
Here given λ= d/2
Initial path difference is given by
If it is now shifted a distance x then path difference will be
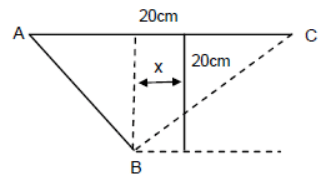
Q.29. Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air = 320 m/s.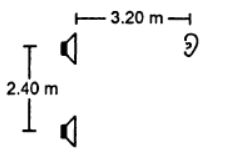
As shown in the figure the path differences 2.4
Q.30. The two sources of sound, S1 and S2, emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S1 S2 and at a distance of 20.0 cm from it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in detector should be shifted to detect a minimum of sound.
Given:
Wavelength of sound wave λ = 20 cm
Separation between the two sources AC = 20cm
Distance of detector from source BD = 20 cmIf the detector is moved through a distance x, then the path difference of the sound waves from sources A and C reaching B is given by:
Path difference = AB − BC
To hear the minimum, this path difference should be equal to:
So,
On solving, we get, x = 12.6 cm.
Hence, the detector should be shifted by a distance of 12.6 cm.
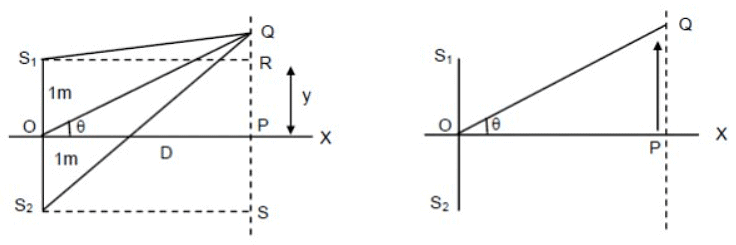
Q.31. Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = -1.0 m (See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m/s.
(a) At what angle θ will the intensity of sound drop to a minimum for the first time?
(b) At what angle will he hear a maximum of sound intensity for the first time?
(c) If he continues to walk along the line, how many more maxima can he hear?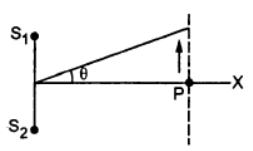
Given:
Frequency of source f = 600 Hz
Speed of sound in air v = 330 m/s
Let the man travel a distance of (y) parallel to the y-axis and let (d) be the distance between the two speakers. The man is standing at a distance of (D) from the origin.
The path difference (x) between the two sound waves reaching the man is given by:
Angle made by man with the origin:
θ = y/D
Given:
d = 2 m
(a) For minimum intensity: The destructive interference of sound (minimum intensity) takes place if the path difference is an odd integral multiple of half of the wavelength.
(b) For maximum intensity: The constructive interference of sound (maximum intensity) takes place if the path difference is an integral multiple of the wavelength.
(c) The more number of maxima is given by the path difference:
He will hear two more maxima at 32° and 64° because the maximum value of θ may be 90°.
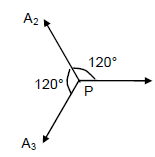
Q.32. Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?
Because the 3 sources have equal intensity, amplitude are equal
So, A1 = A2 = A3
As shown in the figure, amplitude of the resultant = 0 (vector method)
So, the resultant, intensity at B is zero.
Q.33. Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.
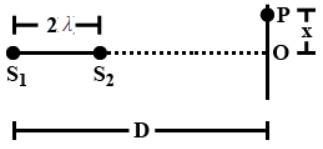
Given:
S1& S2 are in the same phase. At O, there will be maximum intensity.
There will be maximum intensity at P.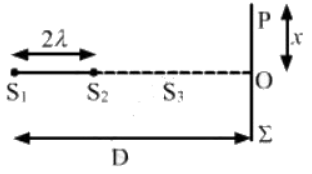
(λ2 is small and can be neglected)
For constructive interference, path difference = nλ
So,
When n = 1,
x = √3D (1st order).
When n =2,
x = 0 ( 2nd order ).
So, when x = √3D, the intensity at P is equal to the intensity at O.
Q.34. Figure shows two coherent sources S1 and S2 which emit sound of wavelength O in phase. The separation between the sources is 3λ. A circular wire of large radius is placed is such a way that S1 S2 lies in its plane and middle point of S1S2 is at the centre of the wire. Find the angular position θ on the wire for which constructive interference takes place.
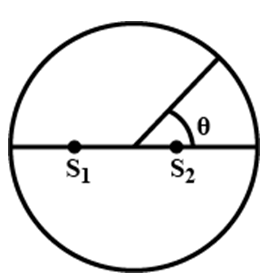
Let the sound waves from the two coherent sources S1 and S2 reach the point P.
rework
OQ = R cosθ
OP = R cosθ
OS2 = OS1 = 1.5λ
From the figure, we find that:
Path difference between the sound waves reaching point P is given by:
Suppose, for constructive interference, this path difference be made equal to the integral multiple of λ.
Hence,
where, n = 0, 1, 2, ...
⇒ θ = 0°, 48.2°, 70.5°and 90° are similar points in other quadrants.
Q.35. Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0.
(a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off?
(b) What will be the answer of the previous part if θ = 60°?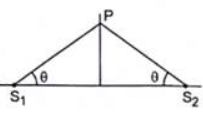
Given:
Resultant intensity at P = I0
The two sources of sound S1 and S2 vibrate with the same frequency and are in the same phase.
(a) When θ = 45°:
Path difference = S1P − S2P = 0So, when the source is switched off, the intensity of sound at P is I0/4.
(b) When θ = 60°, the path difference is also 0. Similarly, it can be proved that the intensity at P is I0/4 when the source is switched off.
Q.36. Find the fundamental, first overtone and second overtone frequencies of an open organ pipe of length 20 cm. Speed of sound in air is 340 ms−1.
Given:
Speed of sound in air v = 340 m/s
Length of open organ pipe L = 20 cm = 20 × 10−2 m
Fundamental frequency (f) of an open organ pipe: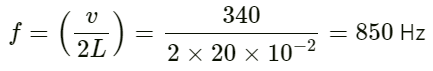
First overtone frequency (f1):
f1 = 2f
Second overtone frequency (f2):
Q.37. A closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air = 340 m s−1.
Given:
Speed of sound in air v = 340 ms−1
Frequency of closed organ pipe f = 500 Hz
Length of tube L = ?
Fundamental frequency of closed organ pipe is given by:
Q.38. In a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is 328 m s−1, what is the frequency of the source?
Given:
Distance between two nodes = 4 cm
Speed of sound in air v = 328 ms−1
Frequency of source f = ?
Wavelength λ = 2 × 4.0 = 8 cm
v = fλ
Hence, the required frequency of the source is 4.1 KHz.
Q.39. The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
Given:
Separation between the node and anti-node = 25 cm
Speed of sound in air v = 340 ms−1
Frequency of vibration of the air column f = ?
The distance between two nodes or anti-nodes is λ.
We have:
λ/4 = 25 cm
⇒ λ = 100 cm = 1 m
Also,
Hence, the frequency of vibration of the air column is 340 Hz.
Q.40. A cylindrical metal tube has a length of 50 cm and is open at both ends. Find the frequencies between 1000 Hz and 2000 Hz at which the air column in the tube can resonate. Speed of sound in air is 340 m s−1.
Given:
Length of cylindrical metal tube L = 50 cm
Speed of sound in air v = 340 ms−1
Fundamental frequency (f1)of an open organ pipe:
So, the required harmonics will be in the range of 1000 Hz to 2000 Hz.
f2 = 2 × 340 = 680 Hz
f3 = 3 × 340 = 1020 Hz
f4 = 4 × 340 = 1360 Hz
f5 = 5 × 340 = 1700 Hz
f6 = 6 × 340 = 2040 Hz
f2, f3, f4... are the second, third, fourth overtone, and so on.
The possible frequencies between 1000 Hz and 2000 Hz are 1020 Hz, 1360 Hz and 1700 Hz.
Q.41. In a resonance column experiment, a tuning fork of frequency 400 Hz is used. The first resonance is observed when the air column has a length of 20.0 cm and the second resonance is observed when the air column has a length of 62.0 cm.
(a) Find the speed of sound in air.
(b) How much distance above the open end does the pressure node form?
Given:
Length of air column at first resonance L1 = 20 cm = 0.2 m
Length of air column at second resonance L2 = 62 cm = 0.62 m
Frequency of tuning fork f = 400 Hz
(a) We know that:
λ =2(L2 − L1)
⇒ λ = 2(62 − 20) = 84 cm = 0.84 m
v = λf,
where v is the speed of the sound in air.
So,
v = 0.84 × 400 = 336 m/s
Therefore, the speed of the sound in air is 336 m/s.
(b) Distance of open node is d:
Therefore, the required distance is 1 cm.
Q.42. The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
Given:
Length of closed organ pipe L1 = 30 cm
Length of open organ pipe L2 = ?
Let f1 and f2 be the frequencies of the closed and open organ pipes, respectively.
The first overtone frequency of a closed organ pipe P1 is given by
where v is the speed of sound in air.
On substituting the respective values, we get:
Fundamental frequency of an open organ pipe is given by:
As per the question,
∴ The length of the pipe P2 will be 20 cm.
Q.43. A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
Length of copper rod l = 1.0 m
Speed of sound in copper v = 3.8 kms−1 = 3800 m/s
Let f be the frequency of the longitudinal waves.
Wavelength (λ) will be :
λ/2 = I
⇒ λ = 2I = 2 × 1 = 2 m
We know that:
v = fλ
⇒ f = v/λ
So,
f = 3800/2 = 1.9 KHz
Therefore, the frequencies between 20 Hz and 20 kHz that will be heard are
= n × 1.9 kHz,
where n = 0, 1, 2, 3, ...10.
Q.44. Find the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20 − 20,000 Hz). Speed of sound in air = 340 m s−1.
Given:
Speed of sound in air v = 340 ms−1
We are considering a minimum fundamental frequency of f = 20 Hz,
since, for maximum wavelength, the frequency is a minimum.
Length of organ pipe l = ?
We have :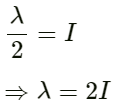
We know that :
On substituting the respective values in the above equation, we get :
Length of the organ pipe is 8.5 m.
Q.45. An open organ pipe has a length of 5 cm.
(a) Find the fundamental frequency of vibration of this pipe.
(b) What is the highest harmonic of such a tube that is in the audible range?
Speed of sound in air is 340 m s−1 and the audible range is 20-20,000 Hz.
Given:
Length of organ pipe L = 5 cm = 5 × 10−2 m
v = 340 m/s
The audible range is from 20 Hz to 20,000 Hz.
The fundamental frequency of an open organ pipe is: f = v/2L
On substituting the respective values, we get:
(b) If the fundamental frequency is 3.4 kHz, then the highest harmonic in the audible range (20 Hz - 20 kHz) is
Required highest harmonic = 20,000/3400 = 5.8 = 5
Q.46. An electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air = 320 m s−1.
Given:
Length of air column in the tube l = 80 cm = 80 × 10−2 m
Speed of sound in air v = 320 ms−1
The frequency of the loudspeaker can be varied between 20 Hz to 2 KHz.
The resonance column apparatus is equivalent to a closed organ pipe.
Fundamental note of a closed organ pipe is given by :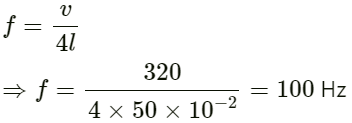
So, the frequency of the other harmonics will be odd multiples of f = (2n + 1)100 Hz.
According to the question, the harmonic should be between 20 Hz and 2 kHz.
∴ n = (0, 1, 2, 3, 4, 5, ..... 9)
Q.47. Two successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324 ms−1.
Given:
Velocity of sound in air v = 324 ms−1
Let l be the length of the resonating column.
Then, the frequencies of the two successive resonances will be
As per the question,
So,
Hence, the length of the tube is 25 cm.
Q.48. A piston is fitted in a cylindrical tube of small cross section with the other end of the tube open. The tube resonates with a tuning fork of frequency 512 Hz. The piston is gradually pulled out of the tube and it is found that a second resonance occurs when the piston is pulled out through a distance of 32.0 cm. Calculate the speed of sound in the air of the tube.
Given:
Frequency of tuning fork f = 512 Hz
Let the speed of sound in the tube be v.
Let l1 be the length at which the piston resonates for the first time and l2 be the length at which the piston resonates for the second time.
We have:
l2 = 2l1 = 2 ×32 = 64 cm = 0.64 m
Velocity v = f × l2
⇒ v = 512 × 0.64 = 328 m/s
Hence, the speed of the sound in the tube is 328 m/s.
Q.49. A U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns. Neglect any end effect and assume that the speed of sound in air = 330 m s−1.
Given:
Speed of sound in air v = 330 ms−1
Frequency of the tuning fork f = 440 Hz
For the shorter arm:
Let the length of the shorter arm of the tube be L1.
Frequency of fundamental mode is given by :
On substituting the respective values, we get:
For the longer arm:
Let the length of the longer arm of the tube be L2 .
Frequency of the first overtone f = 440 Hz
Frequency of the first overtone is given by :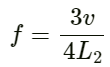
On substituting the respective values, we get:
Q.50. Consider the situation shown in the figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
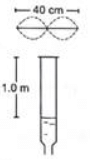
Given:
Speed of sound in air v = 340 ms−1
Length of the wire l = 40 cm = 0.4 m
Mass of the wire M = 4 g
Mass per unit length of wire (m) is given by :
n0 = frequency of the tuning fork
T = tension of the string
Fundamental frequency :
For second harmonic,
On substituting the respective values in equation (i), we get :
Hence, the tension in the wire is 11.6 N.
Q.51. A 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode. A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air = 340 m s−1.
Given:
Mass of long wire M = 10 gm = 10 × 10−3
Length of wire l = 30 cm = 0.3 m
Speed of sound in air v = 340 m s−1
Mass per unit length (m) is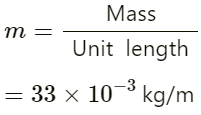
Let the tension in the string be T.
The fundamental frequency n0 for the closed pipe is
The fundamental frequency n0 is given by:
On substituting the respective values in the above equation, we get :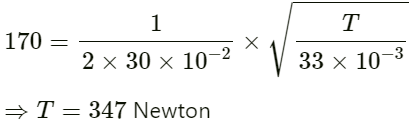
Hence, the tension in the wire is 347 N.
Q.52. Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where 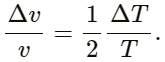
Let f be the frequency of an open pipe at a temperature T. When the fundamental frequency of an organ pipe changes from v to v + ∆v, the temperature changes from T to T + ∆T.
We know that :
According to the question,
Applying this in equation (i), we get:
By expanding the right-hand side of the above equation using the binomial theorem, we get:
Q.53. The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
Given:
The fundamental frequency of a closed pipe is 293 Hz. Let this be represented by f1.
Temperature of the air in closed pipe T1 = 20°C = 20 + 273 = 293 K
Let f2 be the frequency in the closed pipe when the temperature of the air is T2.
∴ T2 = 22°C = 22 + 273 = 295 K
Relation between f and T: f ∝ √T
Q.54. A Kundt's tube apparatus has a copper rod of length 1.0 m clamped at 25 cm from one of the ends. The tube contains air in which the speed of sound is 340 m s−1. The powder collects in heaps separated by a distance of 5.0 cm. Find the speed of sound waves in copper.
Given:
Speed of sound in air vair = 340 ms−1
Velocity of sound in Kundt's tube vrod = ?
Length at which copper rod is clamped l = 25 cm = 25 m × 10−2 m
Distance between the heaps ∆l = 5 cm = 5 × 10−2 m
On substituting the respective values in the above equation, we get:
⇒ vrod = 3400 m/s
Q.55. A Kundt's tube apparatus has a steel rod of length 1.0 m clamped at the centre. It is vibrated in its fundamental mode at a frequency of 2600 Hz. The lycopodium powder dispersed in the tube collects into heaps separated by 6.5 cm. Calculate the speed of sound in steel and in air.
Given :
Length at which steel rod is clamped l = m 12=0.5 m
Fundamental mode of frequency f = 2600 Hz
Distance between the two heaps ∆l = 6.5 cm = 6.5 × 10−2 m
Since Kundt's tube apparatus is a closed organ pipe, its fundamental frequency is given by :
Q.56. A source of sound with adjustable frequency produces 2 beats per second with a tuning fork when its frequency is either 476 Hz of 480 Hz. What is the frequency of the tuning fork?
Given:
First Frequency f1 = 476 Hz
Second frequency f2 = 480 Hz
Number of beats produced per second by the tuning fork m = 2
As the tuning fork produces 2 beats, its frequency should be an average of two.
This is given by :
Q.57. A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
Frequency of tuning fork A : n1 = 256 Hz
No. of beats/second m = 4
Frequency of second fork B : n2 =?
n2 = n1 ± m
⇒ n2 = 256 ± 4
⇒ n2 = 260 Hz or 252 Hz
Now, as it is loaded with wax, its frequency will decrease.
As it produces 6 beats per second, the original frequency must be 252 Hz.
260 Hz is not possible because on decreasing the frequency, the beats per second should decrease, which is not possible.
Q.58. Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
For source A:
Wavelength λ = 32 cm = 32 × 10-2 m
Velocity v = 350 ms-1
Frequency (n1) is given by :
For source B:
Velocity v = 350 ms−1
Wavelength λ = 32.2 cm = 32.2 × 10-2 m
Frequency (n2) is given by:
∴ Beat frequency = 1093.75 − 1086.96 = 6.79 Hz ≈ 7 Hz
Q.59. A tuning fork of unknown frequency makes 5 beats per second with another tuning fork which can cause a closed organ pipe of length 40 cm to vibrate in its fundamental mode. The beat frequency decreases when the first tuning fork is slightly loaded with wax. Find its original frequency. The speed of sound in air is 320 m s−1.
Given:
Length of the closed organ pipe L = 40 cm = 40 × 10−2 m
Velocity of sound in air v = 320 ms−1
Frequency of the fundamental note of a closed organ pipe (n) is given by : n = v/4L
As the tuning fork produces 5 beats with the closed pipe, its frequency must be 195 Hz or 205 Hz.
The frequency of the tuning fork decreases as and when it is loaded. Therefore, the frequency of the tuning fork should be 205 Hz.
Q.60. A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire B produces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
Mass per unit length of both the wires = m
Fundamental frequency of wire of length (l) and tension (T) is given by :
It is clear from the above relation that as the tension increases, the frequency increases.
Fundamental frequency of wire A is given by:
Fundamental frequency of wire B is given by:
It is given that 6 beats are produced when the tension in A is increased.
Therefore, the ratio can be obtained as:
Q.61. A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
Given:
Length of the wire l = 25 cm = 25 × 10−2 m
Frequency of tuning fork f = 256 Hz
Let T be the tension and m the mass per unit length of the wire.
Frequency of the fundamental note in the wire is given by :
It is clear from the above relation that by shortening the length of the wire, the frequency of the vibrations increases.
In the first case:
Let the length of the wire be l1, after it is slightly shortened.
As the vibrating wire produces 4 beats with 256 Hz, its frequency must be 252 Hz or 260 Hz. Again, its frequency must be 252 Hz, as the beat frequency decreases on shortening the wire.
In the second case :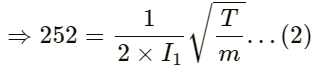
Dividing (2) by (1), we have:
So, it must be shortened by (25 − 24.61)
= 0.39 cm.
Q.62. A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
Velocity of sound in air v = 340 ms−1
Velocity of scooter-driver vo = 36 kmh−1 =
Frequency of sound of whistle fo = 2 kHz
Apparent frequency (f) heard by the scooter-driver approaching the policeman is given by :
Q.63. The horn of a car emits sound with a dominant frequency of 2400 Hz. What will be the apparent dominant frequency heard by a person standing on the road in front of the car if the car is approaching at 18.0 km h−1? Speed of sound in air = 340 m s−1.
Given:
Frequency of sound emitted by horn f0 = 2400 Hz
Speed of sound in air v = 340 ms−1
Apparent frequency of sound (f) is given by:
On substituting the values, we get:
Q.64. A person riding a car moving at 72 km h−1 sound a whistle emitting a wave of frequency 1250 Hz. What frequency will be heard by another person standing on the road
(a) in front of the car
(b) behind the car?
Speed of sound in air = 340 m s−1.
Given:
Frequency of whistle f0 = 1250 Hz
Speed of sound in air v = 340 ms−1
(a) When the car is approaching the person:
Frequency of sound heard by the person (f1) is given by :
On substituting the given values in the above equation, we have:
(b) When the person is behind the car:
Frequency of sound heard by the person (f2) is given by :
On substituting the given values in the above equation, we have :
Q.65. A train approaching a platform at a speed of 54 km h−1 sounds a whistle. An observer on the platform finds its frequency to be 1620 Hz. the train passes the platform keeping the whistle on and without slowing down. What frequency will the observer hear after the train has crossed the platform? The speed of sound in air = 332 m s−1.
Given:
Speed of sound in air v = 332 ms−1
Let
f0 be the original frequency of the train.
When the train approaches a platform, the frequency of sound heard by the observer (f) is given by :
On substituting the values, we have:
When the train crosses the platform, the frequency of sound heard by the observer (f1) is given by :
Substituting the respective values in the above formula, we have:
Q.66. A bat emitting an ultrasonic wave of frequency 4.5 × 104 Hz flies at a speed of 6 m s−1 between two parallel walls. Find the fractional heard by the bat and the beat frequencies heard by the bat and the beat frequency between the two. The speed of sound is 330 m s−1.
Given:
Speed of bat v = 6 ms−1
Frequency of ultrasonic wave f = 4.5 × 104 Hz
Velocity of bird vs = 6 ms−1
Let us assume that the bat is flying between the walls X and Y.
Apparent frequency received by the wall Y is
Now, the apparent frequency received by the bat after reflection from the wall Y is given by:
Frequency of ultrasonic wave received by wall X:
The frequency of the ultrasonic wave received by the bat after reflection from the wall X is
Beat frequency heard by the bat is
= 4.66 × 104 − 4.33 × 104
= 3300 Hz.
Q.67. A bullet passes past a person at a speed of 220 m s−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air = 330 m s−1.
Given:
Velocity of bullet vs = 220 ms−1
Speed of sound in air v = 330 ms−1
Let the frequency of the bullet be f.
Apparent frequency heard by the person (f1) before crossing the bullet is given by:
On substituting the values, we get :
Apparent frequency heard by the person (f2) after crossing the bullet is given by :
On substituting the values, we get :
∴ Fractional change = 1 − 0.2 = 0.8
Q.68. Two electric trains run at the same speed of 72 km h−1 along the same track and in the same direction with separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340 m s−1, find the frequencies heard by the person.
Given:
Speed of sound in air v = 340 ms−1
Frequency of whistles f0 = 500 Hz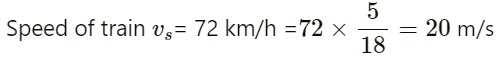
The person will receive the sound in a direction that makes an angle θ with the track. The angle θ is given by :
The velocity of the source will be 'v cos θ' when heard by the observer.
So, the apparent frequency received by the man from train A is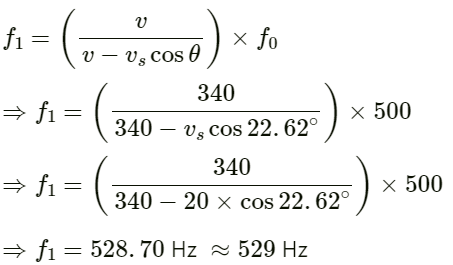
The apparent frequency heard by the man from train B is
Q.69. A violin player riding on a slow train plays a 440 Hz note. Another violin player standing near the track plays the same note. When the two are closed by and the train approaches the person on the ground, he hears 4.0 beats per second. The speed of sound in air = 340 m s−1.
(a) Calculate the speed of the train.
(b) What beat frequency is heard by the player in the train?
Given:
Frequency of violins f0 = 440 Hz
Speed of sound in air v = 340 ms−1
Let the velocity of the train (sources) be vs.
(a) Beat heard by the standing man = 4
∴ frequency (f1) = 440 + 4
= 444 Hz or 436 Hz
Now,
On substituting the values, we have:
(b) The sitting man will listen to fewer than 4 beats/s.
Q.70. Two identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0m s−1 so that he approaches one tuning fork and recedes from the other figure. Find the beat frequency observed by the listener. Speed of sound in air = 332 m s−1.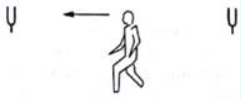
Given:
Speed of sound in air v = 332 ms−1
Velocity of the observer v0 = 3 ms-1
Velocity of the source vs = 0
Frequency of the tuning forks f0 = 256 Hz
The apparent frequency (f1) heard by the man when he is running towards the tuning forks is
On substituting the values in the above equation, we get:
The apparent frequency (f2) heard by the man when he is running away from the tuning forks is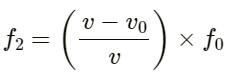
On substituting the values in the above equation, we get :
= 253.7 Hz .
∴ beats produced by them
= f2 − f1
= 258.3 − 253.7 = 4.6 Hz
Q.71. Figure shows a person standing somewhere in between two identical tuning forks. each vibrating at 512 Hz. If both the tuning forks move towards right a speed of 5.5 m s−1, find the number of beats heard by the listener. Speed of sound in air = 330 m s−1.
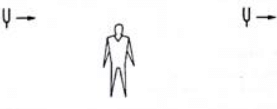
Given:
Frequency of tuning forks f0 = 512 Hz
Speed of sound in air v = 330 ms−1
Velocity of tuning forks vo = 5.5 ms−1
The apparent frequency (f1) heard by the person from the tuning fork on the left is given by:
On substituting the values in the above equation, we get:
Similarly, apparent frequency (f2) heard by the person from the tuning fork on the right is given by:
On substituting the values in the above equation, we get:
∴ beats produced
= f1 − f2
= 520.68 − 503.60 = 17.5 Hz
As the difference is greater than 10 ( persistence of sound for the human ear is 1/10 of a second), the sound gets overlapped and the observer is not able to distinguish between the sounds and the beats.
Q.72. A small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 100/π cm at a constant angular speed of 5.0 revolutions per second. A listener situation situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air = 332 m s−1.
The frequency of the sound, ν = 500 Hz.
The radius of the circle, r = 100/π cm =1/π m.
Angular speed ⍵ = 5 * 2π rad/s = 10π rad/s.
Hence the magnitude of the instantaneous velocity of the source, u = ⍵r = 10π * 1/π m/s = 10 m/s.
As it is clear from the diagram below, the maximum apparent frequency will be observed by the listener when the direction of the velocity is towards him, i.e. at A.
Similarly, the minimum frequency will be observed at B when the direction of the source is away from him.
In both the cases, the observer is stationary and the source is moving. Hence the apparent frequency heard when the source is at A ν' = Vν/(V - u) = 332 * 500/(332 - 10) Hz = 332 * 500/322 Hz ≈ 515 Hz
The apparent frequency heard when the source is at B
ν" = Vν/(V + u)
= 332 * 500/(332 + 10) Hz
= 332 * 500/342 Hz ≈ 485 Hz
Q.73. Two trains are travelling towards each other both at a speed of 90 km h−1. If one of the trains sounds a whistle at 500 Hz, what will be the apparent frequency heard in the other train? Speed of sound in air = 350 m s−1.
Given:
Velocity of sound in air v = 350 ms−1
Velocity of source vs = 90 km/hour
Velocity of observer v0 = 25 m/s
Frequency of whistle f0 = 500 Hz
Apparent frequency (f) heard by the observer in train B is given by:
On substituting the respective values in the above equation, we get:
The apparent frequency heard in the other train is 577 Hz.
Q.74. A traffic policeman sounds a whistle to stop a car-driver approaching towards him. The car-driver does not stop and takes the plea in court that because of the Doppler shift, the frequency of the whistle reaching him might have gone beyond the audible limit of 25 kHz and he did not hear it. Experiments showed that the whistle emits a sound with frequency closed to 16 kHz. Assuming that the claim of the driver is true, how fast was he driving the car? Take the speed of sound in air to be 330 m s−1. Is this speed practical with today's technology?
Given:
Frequency of whistle f0 = 16 × 103 Hz
Apparent frequency f = 20 × 103 Hz
(f is greater than that value)
Velocity of source vs = 0
Letv0 be the velocity of the observer.
Apparent frequency (v) is given by :
On substituting the values in the above equation, we get:
(b) This speed is not practically attainable for ordinary cars.
Q.75. A car moving at 108 km h−1 finds another car in front it going in the same direction at 72 km h−1. The first car sounds a horn that has a dominant frequency of 800 Hz. What will be the apparent frequency heard by the driver in the front car? Speed of sound in air = 330 m s−1.
Given:
Velocity of car sounding a horn
Velocity of front car
Frequency of sound emitted by horn f0 = 800 Hz
Velocity of air v = 330 ms−1
Apparent frequency of sound heard by driver in the front car (f) is given by: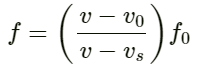
On substituting the values in the above equation, we get:
Q.76. Two submarines are approaching each other in a calm sea. The first submarine travels at a speed of 36 km h−1 and the other at 54 km h−1 relative to the water. The first submarine sends a sound signal (sound waves in water are also called sonar) at a frequency of 2000 Hz.
(a) At what frequency is this signal received from the second submarine. At what frequency is this signal received by the first submarine. Take the speed of of the sound wave in water to be 1500 m s−1.
Given:
Velocity of water v = 1500 m/s
Frequency of sound signal f0 = 2000 Hz
Velocity of first submarine vs = 36 kmh−1
Velocity of second submarine
Frequency received by the first submarine (f1) is given by:
On substituting the values, we get:
(b) Here,
f0 = 2034Hz
Apparent frequency received by second submarine (f2) is given by :
Q.77. A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
Given:
Amplitude r = 17 cm = 17/100 = 0.17 m
Frequency of sound emitted by source f = 800 Hz
Velocity of sound v = 340 m/s
Frequency band = f2 − f1= 8 Hz
Here,
f2 and f1 correspond to the maximum and minimum apparent frequencies (Both will be at the mean position because the velocity is maximum).
Solving for vs, we get:
vs = 1.695 m/s
For SHM:
Q.78. A boy riding on his bike is going towards east at a speed of 4√2 m s−1. At a certain point he produces a sound pulse of frequency 1650 Hz that travels in air at a speed of 334 m s−1. A second boy stands on the ground 45° south of east from his. Find the frequency of the pulse as received by the second boy.
Given:
Frequency of pulse produced by the bike f0 = 1650 Hz
Velocity of bike vb = 4√2ms−1
Velocity of sound in air v = 334 ms−1
Frequency of pulse received by the second boy f = ?
Velocity of an observer v0 = 0
Velocity of source will be : vs = vbcosθ
Frequency of pulse received by the second boy is given by:
Q.79. A sound source, fixed at the origin, is continuously emitting sound at a frequency of 660 Hz. The sound travels in air at a speed of 330 m s−1. A listener is moving along the lien x= 336 m at a constant speed of 26 m s−1. Find the frequency of the sound as observed by the listener when he is
(a) at y = − 140 m,
(b) at y = 0 and
(c) at y = 140 m.
Given:
Frequency of sound emitted by the source n0 = 660 Hz
Velocity of sound in air v = 330 ms-1
Velocity of observer v0 = 26 ms−1
Frequency of sound heard by observer n = ?
(a) At y = 140 m:
Frequency of sound heard by the listener, when the source is fixed but the listener is moving towards the source:
On substituting the values, we get:
(b) When the observer is at y = 0, the velocity of the observer with respect to the source is zero. Therefore, he will hear at a frequency of 660 Hz.
(c) When the observer is at y = 140 m:
On substituting the values, we get:
Q.80. A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear?
(b) What frequency will a person standing near the track hear whom the train has just passed?
(c) A wind starts blowing towards east at a speed of 36 km h−1.
Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
Given:
Velocity of sound in air v = 340 m/s
Velocity of source vs = 108 kmh-1 =
Frequency of the source n0 = 500 Hz
(a) Since the velocity of the passenger with respect to the train is zero, he will hear at a frequency of 500 Hz.
(b) Since the observer is moving away from the source while the source is at rest:
Velocity of observer vo = 0
Frequency of sound heard by person standing near the track is given by:
Substituting the values, we get:
(c) When medium (wind) starts blowing towards the east:
Velocity of medium
The frequency heard by the passenger is unaffected (= 500 Hz).
However, frequency heard by person standing near the track is given by:
Q.81. A boy riding on a bicycle going at 12 km h−1 towards a vertical wall whistles at his dog on the ground. If the frequency of the whistle is 1600 Hz and the speed of sound in air is 330 m s−1, find
(a) the frequency of the whistle as received by the wall
(b) the frequency of the reflected whistle as received by the boy.
Given:
Velocity of sound in air v = 330 ms−1
(a) Frequency of whistle n0 = 1600 Hz
Velocity of an observer v0 = 0 ms−1
Frequency of whistle received by wall n =?
Frequency of sound received by the observer is given by :
On substituting the respective values in the above formula, we get :
(b) Here,
Velocity of observer
Velocity of source vs = 0
Frequency of source n0= 1616 Hz
Frequency of sound heard by observer is
On substituting the respective values in the above formula, we get :
Q.82. A person standing on a road sends a sound signal to the driver of a car going away from him at a speed of 72 km h−1. The signal travelling at 330 m s−1 in air and having a frequency of 1600 Hz gets reflected from the body of the car and returns. Find the frequency of the reflected signal as heard by the person.
Given:
Velocity of sound in air v = 330 ms−1
Frequency of signal emitted by the source n0 = 1600 Hz
As the sound gets reflected, therefore:
Velocity of source ( vs ) = Velocity of observer ( vL )
Velocity of sound heard by the observer is given by :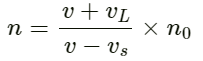
On substituting the values, we get :
The frequency of the reflected signal as heard by the person is 1417 Hz.
Q.83. A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1.
(a) Find the wavelength of the sound emitted by the horn in front of the car.
(b) Find the wavelength of the wave reflected from the cliff.
(c) What frequency does a person sitting in the car hear for the reflected sound wave?
(d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
Given:
Frequency of the car f = 400 Hz
Velocity of sound in air vair = 335 ms−1
Wavelength in front of the car λ =?
(a) Net velocity in front of the car v = vair − vair = 335 − 15 = 320 m/s
(b) The frequency (f1) heard near the cliff is given by :
(c) Here,
Frequency of the reflected sound wave (f2) heard by the person sitting in the car :
(d) He will not hear any beat in 10 seconds because the difference of frequencies is greater than 10 (persistence of sound for the human ear is 1/10 of a second).
Q.84. An operator sitting in his base camp sends a sound signal of frequency 400 Hz. The signal is reflected back from a car moving towards him. The frequency of the reflected sound is found to be 410 Hz. Find the speed of the car. Speed of sound in air = 324 m s−1.
Given:
Velocity of sound in air v = 324 ms−1
Frequency of sound sent by source n0 = 400 Hz
Let the speed of the car be x m/s.
The frequency of sound heard at the car n is given by :
If n1 is the frequency of sound heard by the operator, then its value is given by :
On substituting the value of n from equation (1), we have :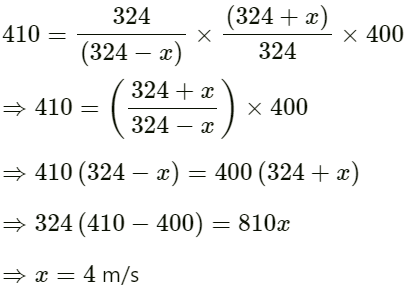
The speed of the car is 4 m/s.
Q.85. Figure shows a source of sound moving along X-axis at a speed of 22 m s−1 continuously emitting a sound of frequency 2.0 kHz which travels in air at a speed of 330 m s−1. A listener Q stands on the Y-axis at a distance of 330 m from the origin. At t = 0, the sources crosses the origin P.
(a) When does the sound emitted from the source at P reach the listener Q?
(b) What will be the frequency heard by the listener at this instant?
(c) Where will the source be at this instant?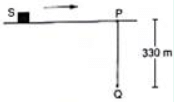
Given:
Velocity of sound in air v = 330 ms−1
Distance travelled by the sound s = 330 m
Frequency of the sound n = 2 kHz
(a) Velocity v = s/t
∴ Time t = 330/330 = 1s
(b) The frequency of sound heard by the listener is 2 kHz.
(Since frequency does not depend on distance.)
(c) s = 22 m (= 22 m/s × 1 s) away from P on x-axis.
Q.86. A source emitting sound at frequency 4000 Hz, is moving along the Y-axis with a speed of 22 m s−1. A listener is situated on the ground at the position (660 m, 0). Find the frequency of the sound received by the listener at the instant the source crosses the origin. Speed of sound in air = 330 m s−1.
Given:
Speed of sound in air v = 330 ms−1
Frequency of sound f0 = 4000 Hz
Velocity of source vs = 22 m/s
The apparent frequency heard by the listener (f) = ?At t = 0, let the source be at a distance of y from the origin. Now, the time taken by the sound
to reach the listener is the same as the time taken by the sound to reach the origin.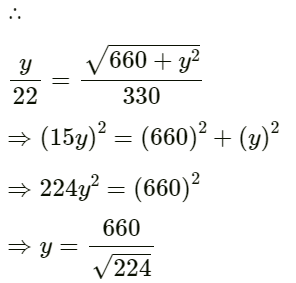
Velocity of source along the line joining the source (S) and listener (L) :
Frequency heard by the listener (f) is
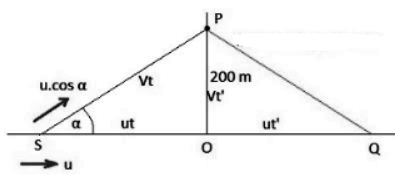
Q.87. A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170 m s−1. A detector is placed at a distance 200 m from the line of motion of the source.
(a) Find the frequency of sound receive by the detector at the instant when the source gets closest to it.
(b) Find the distance between the source and the detector at the instant in detects the frequency 1200 Hz. Velocity of sound in air = 340 m s−1.
Given:
Velocity of the source vs = 170 m/s
Frequency of the source f0 = 1200Hz
(a)
As shown in the figure,
the time taken by the sound to reach the listener is the same as the time taken by the sound to reach the point of intersection.
Frequency of source will be :
The frequency of sound (f) heard by the detector is given by :
(b) The detector will detect a frequency of 1200 Hz at a minimum distance.
Q.88. A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point.
(a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer.
(b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.

Given:
Frequency of sound emitted by the source f0 = 500 Hz
Velocity of sound in air v = 330 ms-1
Radius of the circle r = 1.6 m
Frequency of sound heard by the observer v, = ?(a) Velocity of source at highest point of the circle A is given by :
The frequency of sound heard by the observer when the source is at point C :
Substituting the values, we get :
Frequency of sound observed by the observer when the source is at point A :
Therefore, maximum frequency heard by the observer is 514 Hz.
(b) Velocity at B is given by :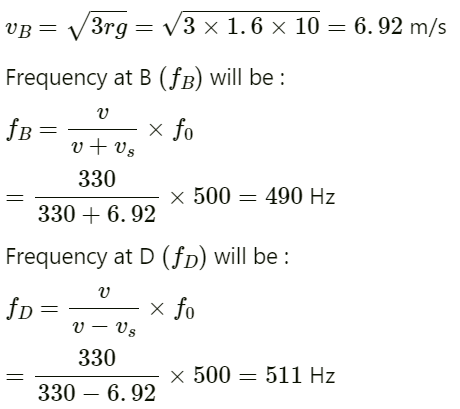
Q.89. A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
Let d be the initial distance between the source and the observer.
If v is the speed of sound emitted by the observer, then the time taken by the sound to reach the observer is given by:
T1 = d/v
The source is also moving. Therefore, at t = T, it moves a distance of (s) and is given by :
Time taken by the pulse to reach the observer :
Time difference (∆t) between the two pulses :
the apparent frequency will be:
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 16: Sound Waves- 2 - HC Verma Solutions - JEE
| 1. What are sound waves and how do they propagate through a medium? |  |
| 2. How does the frequency of a sound wave affect its pitch? |  |
| 3. What is the difference between infrasound and ultrasound? |  |
| 4. How does the amplitude of a sound wave affect its loudness? |  |
| 5. Can sound travel in a vacuum? |  |