HC Verma Questions and Solutions: Chapter 2- Physics & Mathematics- 1 | HC Verma Solutions - JEE PDF Download
Short Answers
Q.1. Is a vector necessarily changed if it is rotated through an angle?
Yes. A vector is defined by its magnitude and direction, so a vector can be changed by changing its magnitude and direction. If we rotate it through an angle, its direction changes and we can say that the vector has changed.
Q.2. Is it possible to add two vectors of unequal magnitudes and get zero? Is it possible to add three vectors of equal magnitudes and get zero?
No, it is not possible to obtain zero by adding two vectors of unequal magnitudes.
Example: Let us add two vectorsof unequal magnitudes acting in opposite directions. The resultant vector is given by
If two vectors are exactly opposite to each other, then
From the above equation, we can say that the resultant vector is zero (R = 0) when the magnitudes of the vectorsare equal (A = B) and both are acting in the opposite directions.
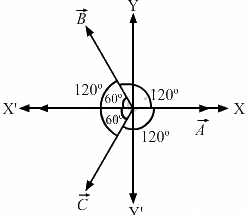
Yes, it is possible to add three vectors of equal magnitudes and get zero.
Lets take three vectors of equal magnitudesgiven these three vectors make an angle of 120° with each other. Consider the figure below:
Lets examine the components of the three vectors.
Here, A = B = C
So, along the x - axis , we have:
Hence, proved.
Q.3. Does the phrase "direction of zero vector" have physical significance? Discuss it terms of velocity, force etc.
A zero vector has physical significance in physics, as the operations on the zero vector gives us a vector.
For any vector
assume that
Again, for any real number λ we have: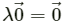
The significance of a zero vector can be better understood through the following examples:
The displacement vector of a stationary body for a time interval is a zero vector.
Similarly, the velocity vector of the stationary body is a zero vector.
When a ball, thrown upward from the ground, falls to the ground, the displacement vector is a zero vector, which defines the displacement of the ball.
Q.4. Can you add three unit vectors to get a unit vector? Does your answer change if two unit vectors are along the coordinate axes?
Yes we can add three unit vectors to get a unit vector.
No, the answer does not change if two unit vectors are along the coordinate axes. Assume three unit vectorsalong the positive x-axis, negative x-axis and positive y-axis, respectively. Consider the figure given below:
The magnitudes of the three unit vectorsare the same, but their directions are different.
So, the resultant ofis a zero vector.
Now,(Using the property of zero vector)
∴ The resultant of three unit vectorsis a unit vector
Q.5. Can we have physical quantities having magnitude and direction which are not vectors?
Yes, there are physical quantities like electric current and pressure which have magnitudes and directions, but are not considered as vectors because they do not follow vector laws of addition.
Q.6. Which of the following two statements is more appropriate?
(a) Two forces are added using triangle rule because force is a vector quantity.
(b) Force is a vector quantity because two forces are added using triangle rule.
Two forces are added using triangle rule, because force is a vector quantity. This statement is more appropriate, because we know that force is a vector quantity and only vectors are added using triangle rule.
Q.7. Can you add two vectors representing physical quantities having different dimensions? Can you multiply two vectors representing physical quantities having different dimensions?
No, we cannot add two vectors representing physical quantities of different dimensions. However, we can multiply two vectors representing physical quantities with different dimensions.
Example: Torque,
Q.8. Can a vector have zero component along a line and still have nonzero magnitude?
Yes, a vector can have zero components along a line and still have a nonzero magnitude.
Example: Consider a two dimensional vectorThis vector has zero components along a line lying along the Y-axis and a nonzero component along the X-axis. The magnitude of the vector is also nonzero. Now, magnitude of
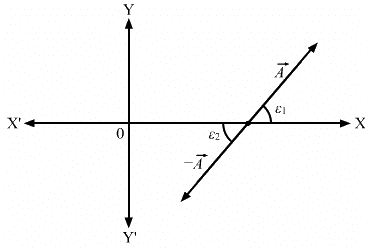
Q.9. Let ε1 and ε2 be the angles made by 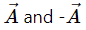 with the positive X-axis. Show that tan ε1 = tan ε2. Thus, giving tan ε does not uniquely determine the direction of
with the positive X-axis. Show that tan ε1 = tan ε2. Thus, giving tan ε does not uniquely determine the direction of 
The direction of -
is opposite to
So, if vector
make the angles ε1 and ε2 with the X-axis, respectively, then ε1 is equal to ε2 as shown in the figure:
Here, tan ε1 = tan ε2
Because these are alternate angles.
Thus, giving tan ε does not uniquely determine the direction of
Q.10. Is the vector sum of the unit vectors 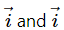 a unit vector? If no, can you multiply this sum by a scalar number to get a unit vector?
a unit vector? If no, can you multiply this sum by a scalar number to get a unit vector?
No, the vector sum of the unit vectors
is not a unit vector, because the magnitude of the resultant of
is not one.
Magnitude of the resultant vector is given by
Yes, we can multiply this resultant vector by a scalar numberto get a unit vector.
Q.11. Let 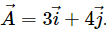 Write a vector
Write a vector 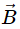 such that
such that 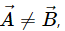 but A = B.
but A = B.
A vector
such that
but A = B are as follows:
Q.12. Can you have 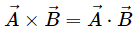 with A ≠ 0 and B ≠ 0 ? What if one of the two vectors is zero?
with A ≠ 0 and B ≠ 0 ? What if one of the two vectors is zero?
No, we cannot have
with A ≠ 0 and B ≠ 0. This is because the left hand side of the given equation gives a vector quantity, while the right hand side gives a scalar quantity. However, if one of the two vectors is zero, then both the sides will be equal to zero and the relation will be valid.
Q.13. If 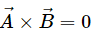 can you say that
can you say that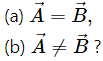
If
then both the vectors are either parallel or antiparallel, i.e., the angle between the vectors is either
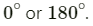
Both the conditions can be satisfied:
(a)i.e., the two vectors are equal in magnitude and parallel to each other
(b)i.e., the two vectors are unequal in magnitude and parallel or anti parallel to each other.
Q.14. Let 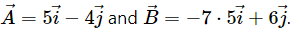 Do we have
Do we have 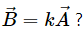 Can we say
Can we say 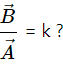
If
then we have
by putting the value of scalar k as
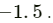
However, we cannot say thatbecause a vector cannot be divided by other vectors, as vector division is not possible.
Multiple Choice Questions
 makes an angle α with
makes an angle α with  and β with
and β with 
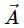 points vertically upward and
points vertically upward and 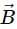 points towards the north. The vector product
points towards the north. The vector product 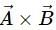 is
is
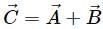
 be 120° and its resultant be
be 120° and its resultant be 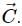
 may be
may be
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 2- Physics & Mathematics- 1 - HC Verma Solutions - JEE
| 1. What are HC Verma Solutions? |  |
| 2. How can HC Verma Solutions help in exam preparation? |  |
| 3. Are HC Verma Solutions available for all chapters of the book? |  |
| 4. Can HC Verma Solutions be used for competitive exams such as JEE and NEET? |  |
| 5. Where can I find HC Verma Solutions for Chapter 2 - Physics & Mathematics- 1? |  |

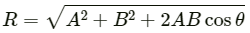
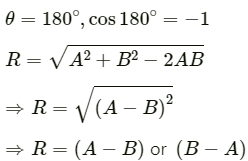
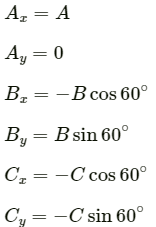
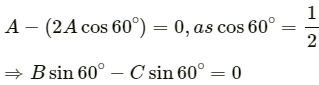
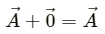
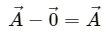
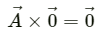
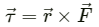
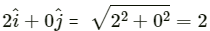
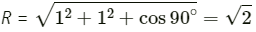

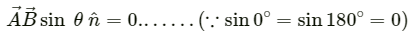
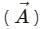 directed towards the north be 5 metres. If we slide it parallel to itself, then the direction and magnitude will not change.
directed towards the north be 5 metres. If we slide it parallel to itself, then the direction and magnitude will not change.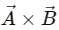 will point towards the west. We can determine this direction using the right hand thumb rule.
will point towards the west. We can determine this direction using the right hand thumb rule.
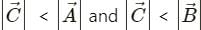
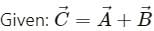
 or the sum of the magnitudes of both the vectors if the two vectors are in opposite directions.
or the sum of the magnitudes of both the vectors if the two vectors are in opposite directions.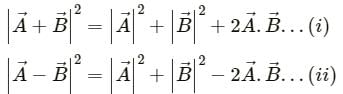
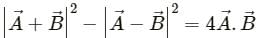
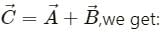
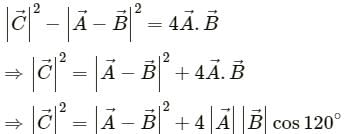
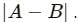
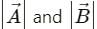 may be less than or equal to AB, or equal to zero, but cannot be greater than AB.
may be less than or equal to AB, or equal to zero, but cannot be greater than AB.




















