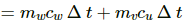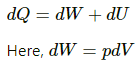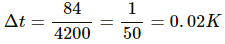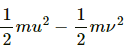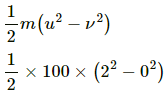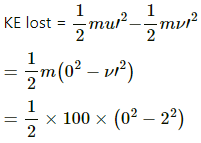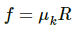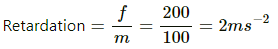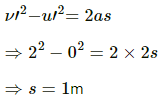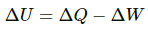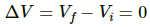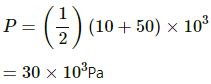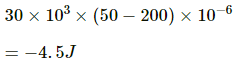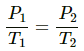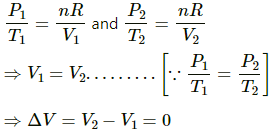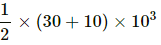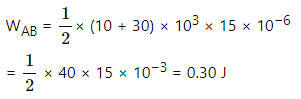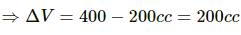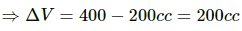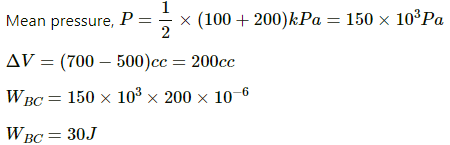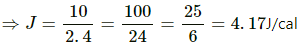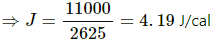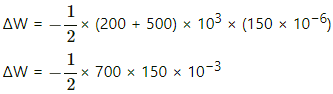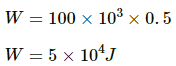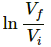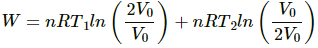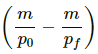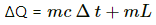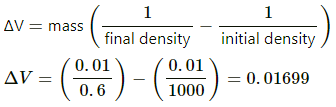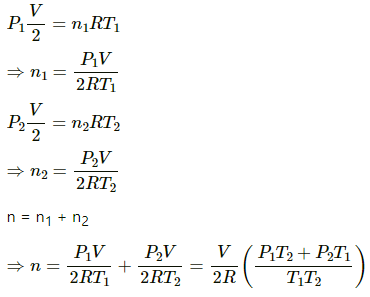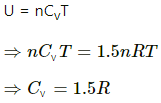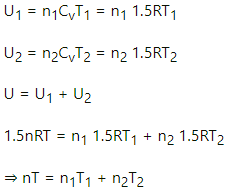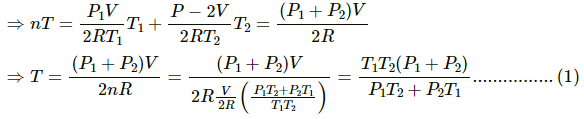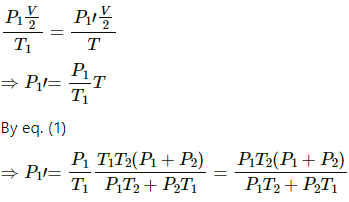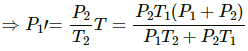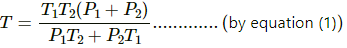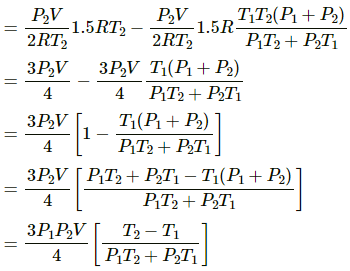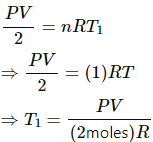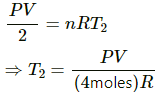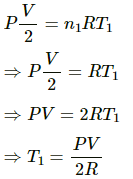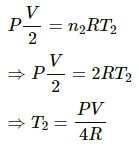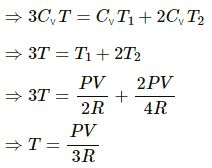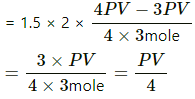HC Verma Questions and Solutions: Chapter 26: Laws of Thermodynamics- 2 | HC Verma Solutions - JEE PDF Download
Exercises
Q.1. A thermally insulated, closed copper vessel contains water at 15°C. When the vessel is shaken vigorously for 15 minutes, the temperature rises to 17°C. The mass of the vessel is 100 g and that of the water is 200 g. The specific heat capacities of copper and water are 420 J kg−1 K−1 and 4200 J kg−1 K−1 respectively. Neglect any thermal expansion. (a) How much heat is transferred to the liquid-vessel system? (b) How much work has been done on this system? (c) How much is the increase in internal energy of the system?
Given:-
The system comprises of an insulated copper vessel that contains water.
t1 = 15°C, t2 = 17°C
t1 is the initial temperature of the system
t2 is the final temperature of the system
∆t = Change in the temperature of the system= t2 − t1
= 17°C − 15°C = 2°C = 275 K
Mass of the vessel, mv = 100 g = 0.1 kg
Mass of water, mw = 200 g = 0.2 kg
Specific heat capacity of copper, cu = 420 J/kg-K
Specific heat capacity of water, cw = 4200 J/kg-K
(a) Since the system is insulated from the surroundings, no heat is transferred between the system and the surroundings. This implies that the heat transferred to the liquid vessel system is zero. The internal heat is shared between the vessel and water.
(b) Work done on the system
⇒ dW = 100 × 10−3 × 420 × 2 + 200 × 10−3 × 4200 × 2
⇒ dW = 84 + 84 × 20 = 84 × 21
⇒ dW = 1764 J
(c) Using the first law of thermodynamics, we get
Work is done by the system. Thus, work done is negative.
⇒ dQ = 0 .............(given)
dU = − dW
= -(-1764) = 1764 J
Q.2. Figure shows a paddle wheel coupled to a mass of 12 kg through fixed frictionless pulleys. The paddle is immersed in a liquid of heat capacity 4200 J K−1 kept in an adiabatic container. Consider a time interval in which the 12 kg block falls slowly through 70 cm. (a) How much heat is given to the liquid? (b) How much work is done on the liquid? (c) Calculate the rise in the temperature of the liquid neglecting the heat capacity of the container and the paddle.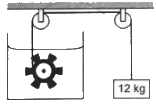
(a) Heat is not given to the liquid; instead, the mechanical work done is converted to heat. Also the container is adiabatic. So, no heat can enter or exit the system. This implies that the heat given to the liquid is zero.
(b) Since the 12 kg mass falls through a distance of 70 cm under gravity, energy is lost by this mass. As this mass is connected to the paddle wheel, energy lost by this mass is gained by the paddle wheel.
⇒">⇒ Work done on the liquid = PE lost by the 12 kg mass
Now,
PE lost by the 12 kg mass = mgh
= 12 × 10 × 0.70
= 84 J
(c) Suppose ∆t is the rise in temperature of the paddle wheel when the system gains energy.
⇒">⇒ 84 = ms∆t
If s is the specific heat of the system, then
84 = 1 × 4200 × ∆t .........(for 'm' = 1 kg)
Q.3. A 100 kg lock is started with a speed of 2.0 m s−1 on a long, rough belt kept fixed in a horizontal position. The coefficient of kinetic friction between the block and the belt is 0.20. (a) Calculate the change in the internal energy of the block-belt system as the block comes to a stop on the belt. (b) Consider the situation from a frame of reference moving at 2.0 m s−1 along the initial velocity of the block. As seen from this frame, the block is gently put on a moving belt and in due time the block starts moving with the belt at 2.0 m s−1. calculate the increase in the kinetic energy of the block as it stops slipping past the belt. (c) Find the work done in this frame by the external force holding the belt.
Here,
m = 100 kg
u = 2.0 m/s
v = 0
μk = 0.2
a) Internal energy of the belt-block system will decrease when the block will lose its KE in heat due to friction. Thus,
KE lost =
= 200 J
b) Velocity of the frame is given by
uf = 2.0 m/s
u’ = u - uf = 2 – 2= 0
v’ = 0 – 2 = -2 m/s
= 200 J
c) Force of friction is given by
rArrf=0.2xxmg=0.2xx100xx10=200N
Distance moved by the block will be as seen from the frame = s
Work done by the force responsible for accelaration as seen from the frame = fs
= 200 x 1 = 200J
Work done by the belt to give it a final velocity of 2 m/s
= 200J
Total work done by external force as seen from the frame 200 + 200 = 400J
Q.4. Calculate the change in internal energy of a gas kept in a rigid container when 100 J of heat is supplied to it.
Given:-
Heat supplied to the system,
ΔQ = 100 J
Using the first law of thermodynamics, we get
Since the container is rigid, initial volume of the system is equal to the final volume of the system. Thus,
∆W = P
∆V = 0
∆U = ∆Q = 100J
We see that heat supplied to the system is used up in raising the internal energy of the system.
Q.5. The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
Initial pressure of the system, P1 = 10 kPa = 10 × 103 Pa
Final pressure of the system, P2 = 50 kPa = 50 × 103 Pa
Initial volume of the system, V1 = 200 cc
Final volume of the system, V2 = 50 cc
(i) Work done on the gas = Pressure × Change in volume of the system
Since pressure is also changing, we take the average of the given two pressures.
Now,
Work done by the system of gas can be given by
(ii) Since no heat is supplied to the system, ∆Q = 0.
Using the first law of thermodynamics, we get
∆U = − ∆W = 4.5 J
Q.6. An ideal gas is taken from an initial state i to a final state f in such a way that the ratio of the pressure to the absolute temperature remains constant. What will be the work done by the gas?
Let:-
P1 = Initial pressure
P2 = Final pressure
T1 = Absolute initial temperature
T2 = Absolute final temperature
Given :-
Using the ideal gas equation, we get
PV = nRT
If n is the number of moles of the gas and R is the universal gas constant, then
Thus, Work done by gas = P∆V = 0
Q.7. Figure shows three paths through which a gas can be taken from the state A to the state B. Calculate the work done by the gas in each of the three paths.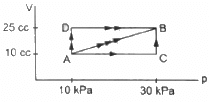
Work done during any process, W = P ∆ V
If both pressure and volume are changing during a process, then work done can be found out by finding the area under the PV diagram.
In path ACB, for line AC :-
Since initial volume is equal to final volume,
∆ V = 0
⇒ WAC = P ∆ V = 0
For line BC :-
P = 30 × 103 pa
WACB = WAC + WBC = 0 + P∆V
= 30 × 103 × (25 − 10) × 10−6
= 0.45 J
For path AB:-
Since both pressure and volume are changing, we use the mean pressure to find the work done.
Mean pressure, P =
Initial volume in path ADB, along line DB is the same as final volume. Thus, work done along this line is zero.
Along line AD, P = 10 kPa
W = WAD + WDB
= 10 × 103 (25 − 10) × 10−6 + 0
= 10 × 15 × 10−3 = 0.15 J
Q.8. When a system is taken through the process abc shown in figure, 80 J of heat is absorbed by the system and 30 J of work is done by it. If the system does 10 J of work during the process adc, how much heat flows into it during the process?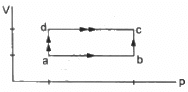
Initial point is a and the final point is c.
As internal energy is a state function so it depends only on the initial and final points and not on the path followed by the system. This implies that change in internal energy for path abc and path adc is the same.
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
Here, ∆Q is the amount of heat absorbed and ∆U is the change in internal energy of the system. Also, ∆W is the work done by the system.
For path abc:-
∆Q = 80 J, ∆W = 30 J
∆U = (80 − 30) J = 50 J
For path abc:-
∆U =50 J ..............(same as for path abc)
∆W = 10 J
∴ ∆Q = 10 J + 50 J = 60 J ..........(∆U = 50 J)
Q.9. 50 cal of heat should be supplied to take a system from the state A to the state B through the path ACB as shown in figure. Find the quantity of heat to be suppled to take it from A to B via ADB.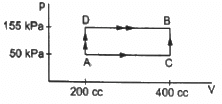
Given:-
In path ACB,
∆Q = 50 cal = (50 × 4.2) J
∆Q = 210 J
∆W = WAC + WCB
Since initial and final volumes are the same along the line BC, change in volume of the system along BC is zero.
Hence, work done along this line will be zero.
For line AC:-
P = 50 kPa
Volume changes from 200 cc to 400 cc.
∆W = WAC + WCB
= 50 × 10−3 × 200 × 10−6 + 0
= 10 J
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
⇒ ∆U = ∆Q − ∆W = (210 − 10) J
∆U = 200 J
In path ADB, ∆Q = ?
∆U = 200 J ..............(Internal energy depends only on the initial and final points and not on the path followed.)
⇒ ∆W = WAD + WDB = ∆W
Work done for line AD will also be zero.
For line DB:-
P = 155 kPa
W = 0 + 155 × 103 × 200 × 10−6
W = 31 J
∆Q = ∆U + ∆W
∆Q= (200 + 31) J = 231 J
∆Q = 55 cal
Q.10. Calculate the heat absorbed by a system in going through the cyclic process shown in figure.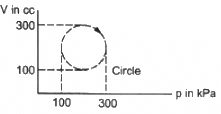
Using the first law of thermodynamics, we get
ΔQ = ΔU + ΔW
Since internal energy depends only on the initial and final points and for a cyclic process, initial and final points are the same, change in internal energy of the system during this process will be zero.
⇒ ΔU = 0
⇒ ΔQ = ΔW
Heat absorbed = Work done
Work done = Area under the graph in the given case
Thus,
Heat absorbed = Area of the circle
Diameter of the circle = 300 - 100 = 200
Heat absorbed = π">π × 104 × 10−6 × 103 J
= 3.14 × 10 = 31.4 J
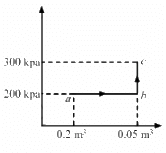
Q.11. A gas is taken through a cyclic process ABCA as shown in figure. If 2.4 cal of heat is given in the process, what is the value of J ?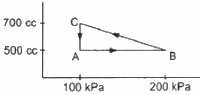
Heat given in the process, ∆Q = 2.4 cal
∆W = WAB + WBC + WCA
For line AB:-
Change in volume,
ΔV = 0
∴ WAB = 0
For line BC :-
For line AC :-
P = 100 kPa
ΔV = 200 cc
WCA = 100 × 103 × 200 × 10−6
Total work done in the one cycle is given by
∆W = 0 + 150× 103 × 200 × 10−6 − 100 × 103 × 200 × 10−6
∆W = 1/2 x 300 × 103 × 200 × 10−6 − 20
∆W = 30 J − 20 J = 10 J
∆U = 0 .............(in a cyclic process)
∆Q = ∆U + ∆W
⇒ 2.4J = 10
Q.12. A substance is taken through the process abc as shown in figure. If the internal energy of the substance increases by 5000 J and a heat of 2625 cal is given to the system, calculate the value of J.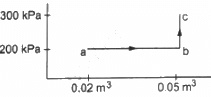
Given:-
Heat given to the system, ∆Q = 2625 cal
Increase in the internal energy of the system, ∆U = 5000 J
From the graph, we get
W = Area of the rectangle formed under line ab + Area under line bc
For line BC:-
Change in volume = 0
WBC = P Δ V = 0
∆W = Area of the rectangle
∆W = 200 × 103 × 0.03
= 6000 J
We know,
∆Q = ∆W + ∆U
⇒ 2625 cal = 6000 J + 5000 J
Q.13. A gas is taken along the path AB as shown in figure. If 70 cal of heat is extracted from the gas in the process, calculate the change in the internal energy of the system.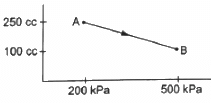
Given:- 70 cal of heat is extracted from the system.
Here,
∆Q = -70 cal = -(70 × 4.2) J = -294 J
From the first law of thermodynamics, we get
∆W = P ∆ V
If P is the average pressure between points A and B and ∆V is the change in volume of the system while going from point A to B, then
∆W = - 525 × 10−1 = - 52.5 J
Here, negative sign is taken because the final volume is less than the initial volume.
∆U = ?
∆Q = ∆U + ∆W
∆Q = - 294 J
Here, negative sign indicates that heat is extracted out from the system.
⇒ − 294 = ∆U - 52.5
⇒ ∆U = − 294 + 52.5 = - 241.5 J
Q.14. The internal energy of a gas is given by U = 1.5 pV. It expands from 100 cm3 to 200 cm3 against a constant pressure of 1.0 × 105 Pa. Calculate the heat absorbed by the gas in the process.
Let change in volume of the gas be ∆V.
∆V = (200 − 100) cm3 = 100 cm3
= 10−4 m3
p = 1 × 105 Pa
Change in internal energy of the system, ∆U = 1.5 pV
∆U = 1.5 × 105 × 10−4 = 15 J
∆W = p∆V
= 105 × 10−4 = 10 J
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W = 10 + 15 = 25 J
Thus, heat absorbed by the system is 25 J.
Q.15. A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
Given:- Heat supplied to the system, ∆Q = 10 J
Change in volume of the system, ∆V = Area of cross section × Displacement of the piston
= A × 10 cm
= (4 × 10) cm3 = 40 × 10−6 m3
P = 100 kPa
∆W = P∆V = 100 × 103 × 40 × 10−6 m3
= 4 J
∆U = ?
Using the first law of thermodynamics, we get
10 = ∆U + ∆W
⇒ 10 = ∆U + 4
⇒ ∆U = 6 J
Here, positive sign indicates that the internal energy of the system has increased.
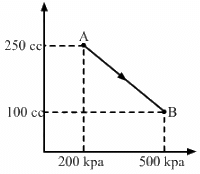
Q.16. A gas is initially at a pressure of 100 kPa and its volume is 2.0 m3. Its pressure is kept constant and the volume is changed from 2.0 m3 to 2.5 m3. Its Volume is now kept constant and the pressure is increased from 100 kPa to 200 kPa. The gas is brought back to its initial state, the pressure varying linearly with its volume. (a) Whether the heat is supplied to or extracted from the gas in the complete cycle? (b) How much heat was supplied or extracted?
(a) Given:-
P1 = 100 kPa,
V1 = 2 m3
V2 = 2.5 m3
∆V = 0.5 m3
Work done, W = P∆V
WAB = Area under line AB = 5 × 104 J
If volume is kept constant for line BC, then ∆V = 0.
WBC = P∆V = 0
Work done while going from point B to C = 0
When the system comes back to the initial point A from C, work done is equal to area under line AC.
WCA = Area of triangle ABC + Area of rectangle under line AB
Total work done, W = Area enclosed by the ABCA
W = WAC - WAB
From the graph, we see that the area under AC is greater than the area under AB. We also see that heat is extracted from the system as change in the internal energy is zero.
(b) Amount of heat extracted = Area enclosed under ABCA
= (1/2) x 0.5 x 100 x 103 = 25000J
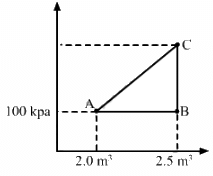
Q.17. Consider the cyclic process ABCA, shown in figure, performed on a sample of 2.0 mol of an ideal gas. A total of 1200 J of heat is withdrawn from the sample in the process. Find the work done by the gas during the part BC.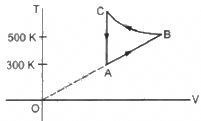
Given:-
Number of moles of the gas, n = 2
∆Q = − 1200 J (Negative sign shows that heat is extracted out from the system)
∆U = 0 ..............(During cyclic process)
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
⇒ −1200 = 0 + (WAB + WBC + WCA)
Since the change in volume of the system applies on line CA, work done during CA will be zero.
From the ideal gas equation, we get
PV = nRT
P∆V = nR∆T
W = P∆V = nR∆T
⇒ ∆Q = ∆U + ∆W
⇒ −1200 = nR∆T + WBC + 0
⇒ −1200 = 2 × 8.3 × 200 + WBC
WBC = − 400 × 8.3 − 1200
= − 4520 J
Q.18. Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.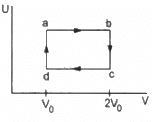
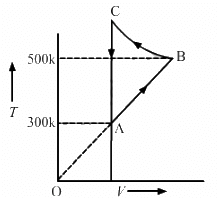
Given: Number of moles of the gas, n = 2 moles
The system's volume is constant for lines bc and da.
Therefore,
∆V = 0
Thus, work done for paths da and bc is zero.
⇒ Wda = Wbc = 0
Since the process is cyclic, ∆U is equal to zero.
Using the first law, we get
∆W = ∆Q
∆W = ∆WAB + ∆WCD
Since the temperature is kept constant during lines ab and cd, these are isothermal expansions.
Work done during an isothermal process is given by
W = nRT
If Vf and Vi are the initial and final volumes during the isothermal process, then
W = nR × 2.303 × log 2 × (500 − 300)
W = 2 × 8.314 × 2.303 × 0.301 × 200
W = 2305.31 J
Q.19. Find the change in the internal energy of 2 kg of water as it is heated from 0°C to 4°C. The specific heat capacity of water is 4200 J kg−1 K−1 and its densities at 0°C and 4°C are 999.9 kg m−3 and 1000 kg m−3 respectively. Atmospheric pressure = 105 Pa.
Given:-
Mass of water, M = 2 kg
Change in temperature of the system, ∆θ = 4°C = 277 K
Specific heat of water, sw = 4200 J/kg-°C
Initial density, p0 = 999.9 kg/m3
Final density, pf = 1000 kg/m3
P = 105 Pa
Let change in internal energy be ∆U.
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
Also, ∆Q = ms∆θ
W = P∆V = P(Vf - Vi)
⇒ ms∆θ = ∆U + P (V0 − V4)
⇒ 2 × 4200 × 4= ∆U + 105 (∆V)
⇒ 33600 = ∆U + 105
⇒ 33600 = ∆U + 105 × ( - 0.0000002)
⇒ 33600 = ∆U - 0.02
∆U = (33600 - 0.02) J
Q.20. Calculate the increase in the internal energy of 10 g of water when it is heated from 0°C to 100°C and converted into steam at 100 kPa. The density of steam = 0.6 kg m−3. Specific heat capacity of water = 4200 J kg−1 °C−1 and the latent heat of vaporization of water = 2.25 × 10 6J kg−1.
Given:-
Mass of water, m = 10 g = 0.01 kg
Pressure, P = 105 Pa
Specific heat capacity of water, c = 1000 J/Kg °C
Latent heat, L = 2.25 × 106 J/Kg
∆ t = Change in temperature of the system = 100°C = 373 K
∆Q = Heat absorbed to raise the temperature of water from 0°C to 100°C + Latent heat for conversion of water to steam
= 0.01 × 4200 × 100 + 0.01 × 2.5 × 106
= 4200 + 25000 = 29200 J
∆W = P∆V
∆W = P∆V = 0.01699 × 105 = 1699 J
Using the first law, we get
∆Q = ∆W + ∆U
∆U = ∆Q − ∆W = 29200 − 1699
= 27501 = 2.75 × 104 J
Q.21. Figure shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5 nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1, T1 on the left and p2, T2 on the right. The system is left for sufficient time so that the temperature becomes equal on the two sides. (a) How much work has been done by the gas on the left part? (b) Find the final pressures on the two sides. (c) Find the final equilibrium temperature. (d) How much heat has flown from the gas on the right to the gas on the left?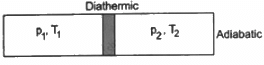
Let n1, U1 and n2, U2 be the no. of moles , internal energy of ideal gas in the left chamber and right chamber respectively.
(a) As the diathermic wall is fixed, so final volume of the chambers will be same. Thus, ΔV = 0, hence work done ΔW= P Δ V = 0 by eq. of state in the first and second chamber
Again,
In the first and second chamber internal energy is given by
b) Let final pressure in the first and second compartment P1' and P2'.
By five variable equ of state in the first chamber
Similarly,
c) Final temperature will be
d) Heat lost by right chamber will be
n2CvT2 - n2CvT
Q.22. An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
(a) Since the conducting wall is fixed, the work done by the gas on the left part during the process is zero because the change in volume will be zero due to the fixed position of the wall.
(b) For left side:-
Let the initial pressure on both sides of the wall be p.
We know,
Volume = V/2
Number of moles, n = 1
Let initial temperature be T1.
Using the ideal gas equation, we get
For right side:-
Number of moles, n = 2
Let the initial temperature be T2.
We know,
Volume = V/2
(c)
Here,
U = 1.5nRT
T = temperature at the equilibrium
P1 = P2 = P
n1 = 1 mol
n2 = 2 mol
Let T1 and T2 be the initial temperatures of the left and right chamber respectively.
Applying eqn. of state
For left side chamber
Right side chamber
We know that total n = n1 + n2 = 3
U1 = n1CvT1 = CvT1
U2 = n2CvT2 = 2CvT2
U =nCvT
U = U1 + U2
(d) For RHS:-
∆Q = ∆U as ∆W = 0
∆U = 1.5 n2R (T − T2)
When T is the final temperature and T2 is the initial temperature of side 1, we get
= 1.5 × 2 × R (T − T2)
(e) If dW = 0, then using the first law, we get
dQ = − dU
⇒ dU = − dQ = (-PV)/4.
|
134 docs
|