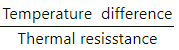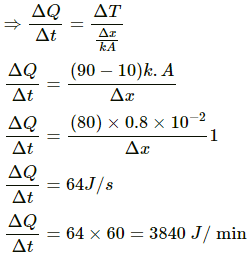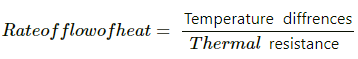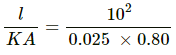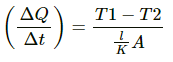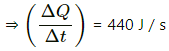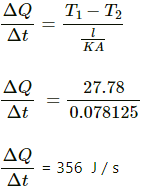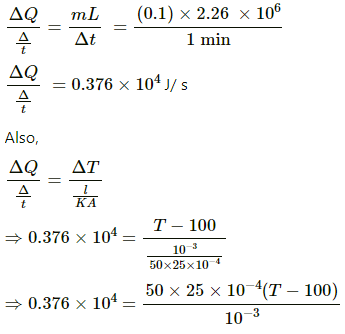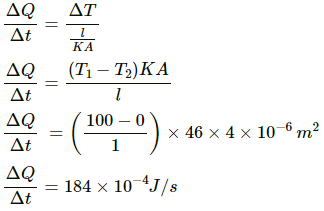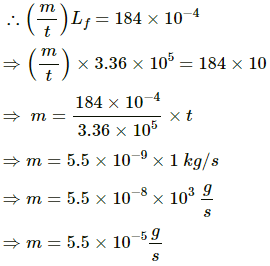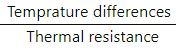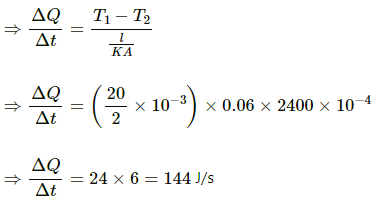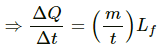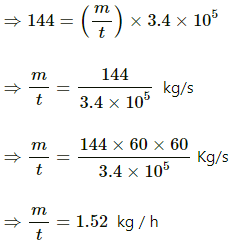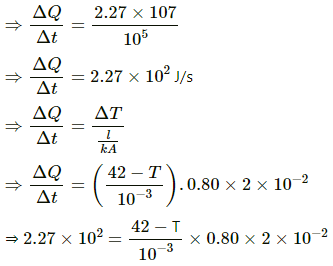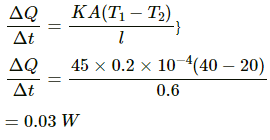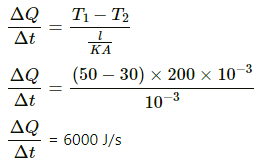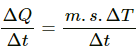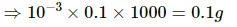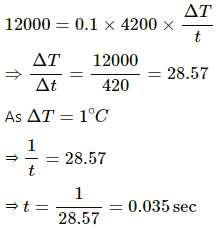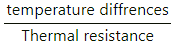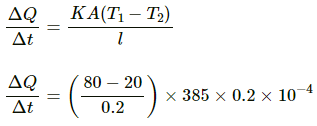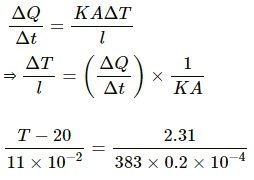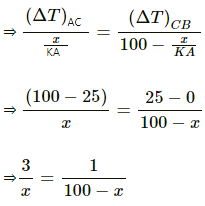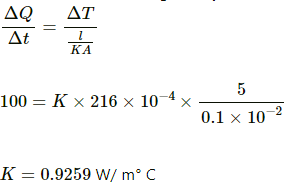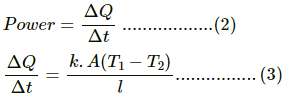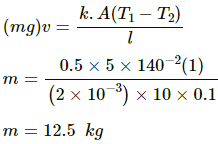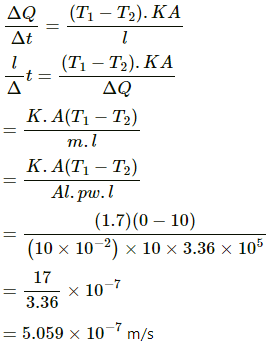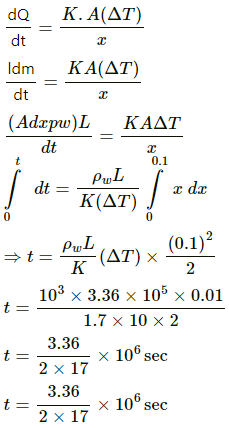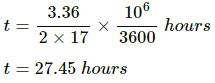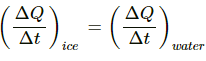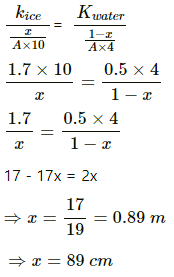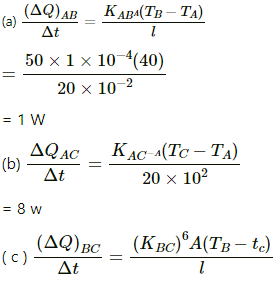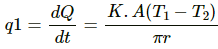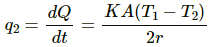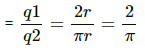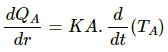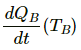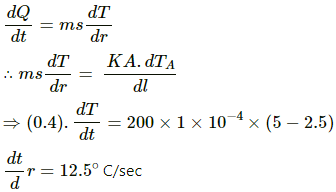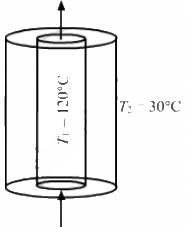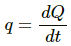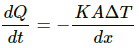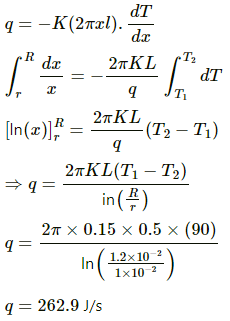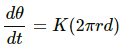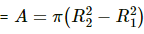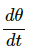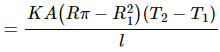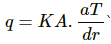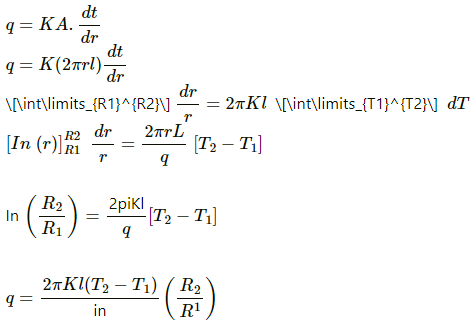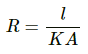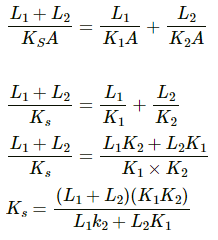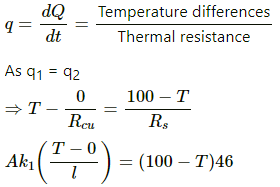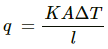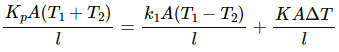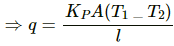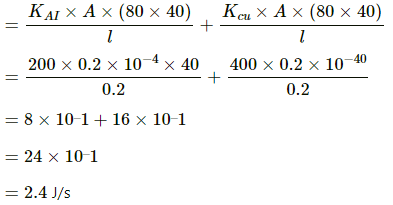HC Verma Questions and Solutions: Chapter 28: Heat Transfer- 2 | HC Verma Solutions - JEE PDF Download

Q.1. A uniform slab of dimension 10 cm × 10 cm × 1 cm is kept between two heat reservoirs at temperatures 10°C and 90°C. The larger surface areas touch the reservoirs. The thermal conductivity of the material is 0.80 W m^?1 °C^?1. Find the amount of heat flowing through the slab per minute.

Given:
Thermal conductivity of the material, k = 0.80 W m^-1  °c^-1
Area of the cross section of the slab, A = 100 cm²  = 10^-2 m²
Thickness of the slab, ?x = 1 cm = 10 ^-2 m
Rate of flow of heat =

Q.2. A liquid-nitrogen container is made of a 1 cm thick styrofoam sheet having thermal conductivity 0.025 J s^?1 m^?1 °C^?1. Liquid nitrogen at 80 K is kept in it. A total area of 0.80 m2 is in contact with the liquid nitrogen. The atmospheric temperature us 300 K. Calculate the rate of heat flow from the atmosphere to the liquid nitrogen.

Thickness of the container, l = 1 cm = 10 ^-2 m
Thermal conductivity of the styrofoam sheet, k = 0.025 J s^-1 m^-1 °C ^-1
Area, A= 0.80 m²
Thermal resistance
Temperature difference , ?T = T₁ - T₂ = 300 - 80 = 220K
Rate of flow of heat,

Q.3. The normal body-temperature of a person is 97°F. Calculate the rate at which heat is flowing out of his body through the clothes assuming the following values. Room temperature = 47°F, surface of the body under clothes = 1.6 m², conductivity of the cloth = 0.04 J s^?1 m^?1°C^?1, thickness of the cloth = 0.5 cm.

Rate of how of heat =
Temperature of the body, T₁ = 97°F= 36. 11°C
Temperature of the surroundings, T₂ = 47°F= 8.33°C`
Conductivity of the cloth, K = 0.04  J s^-1 m^-1  °c
Thickness of the cloth l = 0.5 cm = 0.005 m
Area of the cloth, A=1.6 m²
Difference in the temperature ?T = T₁ - T₂ = 36.11 - 8.33 = 27.78°C
Thermal resistance =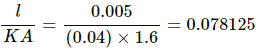  
Rate at which heat is flowing out is given by

Q.4. Water is boiled in a container having a bottom of surface area 25 cm², thickness 1.0 mm and thermal conductivity 50 W m^?1°C^?1. 100 g of water is converted into steam per minute in the steady state after the boiling starts. Assuming that no heat is lost to the atmosphere, calculate the temperature of the lower surface of the bottom. Latent heat of vaporisation of water = 2.26 × 10⁶ J kg^?1.

Area of the bottom of the container, A = 25 cm² = 25 × 10^-4 m²
Thickness of the vaporisation of water , l = 1 mm = 10^-3 m.
Latent heat of vaporisation of water, L = 2.26 × 10⁶  j Kg -1
Thermal conductivity of the container , K =50W m- 1 °C^-1 mass = 100 g = 0.1 Kg  
mass = 100g = 0.11 kg
Rate of heat transfer from the base of the container is given by

? ( T - 100 ) = 3.008 × 10
? T = 130° C.

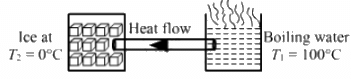
Q.5. One end of a steel rod (K = 46 J s^?1 m^?1°C^?1) of length 1.0 m is kept in ice at 0°C and the other end is kept in boiling water at 100°C. The area of cross section of the rod is 0.04 cm². Assuming no heat loss to the atmosphere, find the mass of the ice melting per second. Latent heat of fusion of ice = 3.36 × 10⁵ J kg^?1.

Given:
Thermal conductivity of the rod, K = 46 J s^–1 m^–1 °C^–1
Length of the rod, l = 1 m
Area of the cross-section of the rod, A =0.04 cm²
= 0.04 × 10^?4 m²
= 4 × 10^?6 m²
Rate of transfer of heat is given by

Also , ?Q = mL_f

Q.6. A icebox almost completely filled with ice at 0°C is dipped into a large volume of water at 20°C. The box has walls of surface area 2400 cm², thickness 2.0 mm and thermal conductivity 0.06 W m^?1°C^?1. Calculate the rate at which the ice melts in the box. Latent heat of fusion of ice =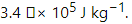

Area of the walls of the box, A = 2400 cm² = 2400 × 10^?4 m²
Thickness of the ice box, l = 2 mm = 2 × 10^?3 m
Thermal conductivity of the material of the box, K = 0.06 W m^?1 °C^?1

Temperature of the water outside the box, T₁ = 20°C

Temperature of ice, T₂ = 0°C
Rate of flow of heat =

Rate at which the ice melts = mL_f/t

Q.7. A pitcher with 1-mm thick porous walls contains 10 kg of water. Water comes to its outer surface and evaporates at the rate of 0.1 g s^?1. The surface area of the pitcher (one side) = 200 cm². The room temperature = 42°C, latent heat of vaporization = 2.27 × 10⁶ J kg^?1, and the thermal conductivity of the porous walls = 0.80 J s^?1 m^?1°C^?1. Calculate the temperature of water in the pitcher when it attains a constant value.

Thickness of porous walls, l = 1mm = 10^-3 m
mass, m =10 kg
Latent heat of vapourisation, Lv = 2.27 × 10⁶ J/kg
Thermal conductivity, K =   0.80 J/m s °C
?Q = 2.27 × 10⁶ × 10 J
0.1 g of water evaporate in 1 sec, so 10 kg water will evaporate in 10⁵ s

? T = 27.8° C
? T = 28° C 

Q.8. A steel frame (K = 45 W m^?1°C^?1) of total length 60 cm and cross sectional area 0.20 cm², forms three sides of a square. The free ends are maintained at 20°C and 40°C. Find the rate of heat flow through a cross section of the frame.

Thermal conductivity, K = 45 W m^–1 °C^–1
Length, l = 60 cm = 0.6 m
Area of cross section, A = 0.2 cm2 = 0.2 × 10^?4 m²
Initial temperature, T₁ = 40°C
Final temperature, T₂ = 20°C
Rate of flow of heat =

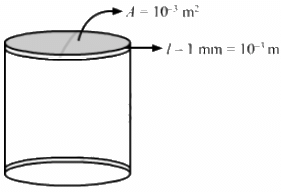
Q.9. Water at 50°C is filled in a closed cylindrical vessel of height 10 cm and cross sectional area 10 cm². The walls of the vessel are adiabatic but the flat parts are made of 1-mm thick aluminium (K = 200 J s^?1 m^?1°C^?1). Assume that the outside temperature is 20°C. The density of water is 100 kg m^?3, and the specific heat capacity of water = 4200 J k^?1g °C^?1. Estimate the time taken for the temperature of fall by 1.0 °C. Make any simplifying assumptions you need but specify them.

Area of cross section, A = 10 cm² = 10 × 10^–4 m²
Thermal conductivity, K = 200 Js^–1 m^–1 °C^–1
Height, H = 10 cm
Length, l = 1 mm =10^–3 m
Temperature inside the cylindrical vessel, T₁ = 50°C
temperature outside the vessel, T₂ = 30°C

Rate of flow of heat from 1 flat surface will be given by

Heat escapes out from both the flat surfaces.
Net rate of heat flow = 2 × 6000 = 12000 J/sec

Mass = Volume density

Using this in the above formula for finding the rate of flow of heat, we get

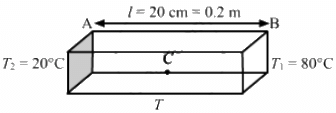
Q.10. The left end of a copper rod (length = 20 cm, area of cross section = 0.20 cm²) is maintained at 20°C and the right end is maintained at 80°C. Neglecting any loss of heat through radiation, find (a) the temperature at a point 11 cm from the left end and (b) the heat current through the rod. Thermal conductivity of copper = 385 W m^?1°C^?1.

Area of cross section, A = 0.2 cm² = 0.2 × 10^?4 m²
Thermal conductivity, k = 385 W m^–1 °C^–1
Rate of flow of heat=

= 2310 × 10^-3
= 2.31 J/sec
Let te temperature of point C be T, which is at a distance of 11 cm from the left end.
Rate of flow of heat is given by

? T = 33 + 20
? T = 53°C

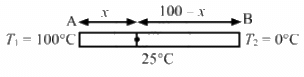
Q.11. The ends of a metre stick are maintained at 100°C and 0°C. One end of a rod is maintained at 25°C. Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?

One end of the rod is at a temperature of 25°C. So, if no heat current flows through the rod in steady state, then the other end of the rod should also be at a temperature of 25°C.
Let the point at which the other end of the rod is touched be C.
No heat flows through the rod when the temperature at point C is also 25°C.
Heat current through AC = Heat current through CB

? 300 - 3x = x
? 300 = 4x
x = 75 cm
Thus, it should be touched at 75 cm from 100°C end.

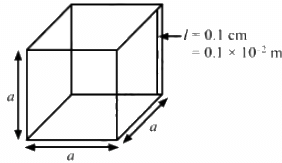
Q.12. A cubical box of volume 216 cm³ is made up of 0.1 cm thick wood. The inside is heated electrically by a 100 W heater. It is found that the temperature difference between the inside and the outside surface is 5°C in steady state. Assuming that the entire electrical energy spent appears as heat, find the thermal conductivity of the material of the box.

Volume of the cube, V = a³ = 216 cm³
Edge of the cube, a = 6 cm
Surface area of the cube = 6a² 
= 6 (6 × 10^?2)²
= 216 × 10^?4 m²
Thickness, l = 0.1 cm = 0.1 × 10^–2 m
Temperature difference, ? T = 5°C
The inner surface of the cube is heated by a 100 W heater.
? Power, P = 100 W
Power = Energy per unit time
? Rate of flow of heat inside the cube, R = 100 J/s
Rate of flow of heat is given by

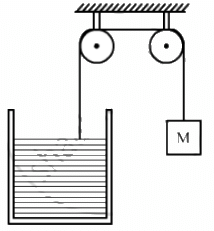
Q.13. Following Figure shows water in a container having 2.0 mm thick walls made of a material of thermal conductivity 0.50 W m^?1°C^?1. The container is kept in a melting-ice bath at 0°C. The total surface area in contact with water is 0.05 m². A wheel is clamped inside the water and is coupled to a block of mass M as shown in the figure. As the block goes down, the wheel rotates. It is found that after some time a steady state is reached in which the block goes down with a constant speed of 10 cm s^?1 and the temperature of the water remains constant at 1.0°C. Find the mass M of the block. Assume that the heat flows out of the water only through the walls in contact. Take g = 10 m s^?2.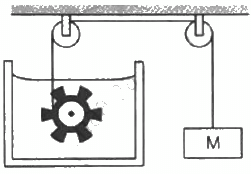

Temperature of water, T₁ = 1°C
Temperature if ice bath, T₂ = 0°C
Thermal conductivity, K = 0.5 W/m °C
Length through which heat is lost, l = 2 mm = 2 × 10^–3 m
Area of cross section, A = 5 × 10^?2 m²
Velocity of the block, v = 10 cm/sec = 0.1 m/s
Let the mass of the block be m.
Power = F · v
= (mg) v          ......(1)
Also,

From equation (1), (2) and (3), we get

Q.14. On a winter day when the atmospheric temperature drops to ?10°C, ice forms on the surface of a lake. (a) Calculate the rate of increase of thickness of the ice when 10 cm of the ice is already formed. (b) Calculate the total time taken in forming 10 cm of ice. Assume that the temperature of the entire water reaches 0°C before the ice starts forming. Density of water = 1000 kg m^?3, latent heat of fusion of ice = 3.36 × 10⁵ J kg^?1 and thermal conductivity of ice = 1.7 W m^?1°C^?1. Neglect the expansion of water of freezing.

Thermal conductivity, K = 1.7 W/m°C
Density of water, ?_? = 10² kg/m³
Latent heat of fusion of ice, L_ice = 3.36 × 10⁵ J/kg
Length, l = 10 × 10^?2 m
(a) Rate of flow of heat is given by

= 5 × 10^-7 m/s
(b) To form a thin ice layer of thickness dx, let the required be dt.
Mass of that thin layer, dm = A dx ?_?
Heat absorbed by that thin layer, dQ = Ldm

Q.15. Consider the situation of the previous problem. Assume that the temperature of the water at the bottom of the lake remains constant at 4°C as the ice forms on the surface (the heat required to maintain the temperature of the bottom layer may come from the bed of the lake). The depth of the lake is 1.0 m. Show that the thickness of the ice formed attains a steady state maximum value. Find this value. The thermal conductivity of water = 0.50 W m^?1°C^?1. Take other relevant data from the previous problem.

Let the point upto which ice is formed is at a distance of x m from the top of the lake.
Under steady state, the rate of flow of heat from ice to this point should be equal to the rate flow of heat from water to this point.
Temperature of the top layer of ice = ?10°C
Temperature of water at the bottom of the lake = 4°C
Temperature at the point upto which ice is formed =

Q.16. Three rods of lengths 20 cm each and area of cross section 1 cm² are joined to form a triangle ABC. The conductivities of the rods are K_AB = 50 J s^?1 m^?1°C^?1, K_BC = 200 J s^?1m^?1°C^?1 and K_AC = 400 J s^?1 m^?1°C^?1. The junctions A, B and C are maintained at 40°C, 80°C and 80°C respectively. Find the rate of heat flowing through the rods AB, AC and BC.

Thermal conductivity of rod AB, K_AB = 50 J/m-s-°C
Temperature of junction at A, T_A = 40°C
Thermal conductivity of rod BC, K_BC = 200 J/m-s-°C
Temperature of junction at B, T_B = 80°C
Thermal conductivity of rod BC, K_CA = 400 J/m-s-°C
temperature of junction at C, T_C = 80°C
l = 20 cm = 20 × 10^?2 m
A = 1 cm² = 10^?4 m²

= 0

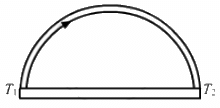
Q.17. A semicircular rod is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the semicircular rod to the heat transferred through a cross section of the straight rod in a given time.

Let A be the area of cross section and K be the thermal conductivity of the material of the rod.
Let q₁ be the rate of flow of heat through a semicircular rod.
Rate of flow of heat is given by

Let q₂ be the rate of flow of heat through a straight rod.

Ratio of the rate of flow of heat through the 2 rods

Q.18. A metal rod of cross sectional area 1.0 cm² is being heated at one end. At one time, the temperatures gradient is 5.0°C cm^?1 at cross section A and is 2.5°C cm^?1 at cross section B. Calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB = 0.40 J°C^?1, thermal conductivity of the material of the rod = 200 W m^?1°C^?1. Neglect any loss of heat to the atmosphere.

Let the temperature

Let the temperatures at the ends A and B be T_A and T_B, respectively.
Rate of flow of heat at end A of the rod is given by

Rate of flow of heat at end B of the rod is given by

Heat absorbed by the rod = ms?T
Here, s is the specific heat of the rod and ?T is the temperature difference between ends A and B.
Rate of heat absorption by the rod is given by

Q.19. Steam at 120°C is continuously passed through a 50 cm long rubber tube of inner and outer radii 1.0 cm and 1.2 cm. The room temperature is 30°C. Calculate the rate of heat flow through the walls of the tube. Thermal conductivity of rubber = 0.15 J s^?1 m^?1°C^?1.

Inner radii = r = 1 cm = 10^–2 m
Outer radii = R = 1.2 cm = 1.2 × 10^–2 m
Length of the tube, l = 50 cm = 0.5 m
Thermal conductivity, k = 0.15 Js–1 m^–1 °C^–1
Top View

Let us consider a cylindrical shell of length l, radius x and thickness dx.
Rate of flow of heat

Here , the negative sign indicates that the rate of heat flow decreases as x increases.

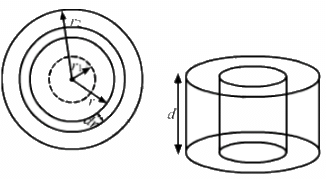
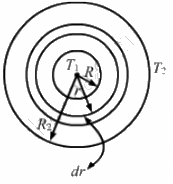
Q.20. A hole of radius r₁ is made centrally in a uniform circular disc of thickness d and radius r₂. The inner surface (a cylinder a length d and radius r₁) is maintained at a temperature ?₁ and the outer surface (a cylinder of length d and radius r₂) is maintained at a temperature ?₂ (?₁ > ?₂). The thermal  conductivity of the material of the disc is K. Calculate the heat flowing per unit time through the disc.

Let  be the rate of flow of heat.
Consider an annular ring of radius r and thickness dr.
Rate of flow of heat is given by

Rate of flow of heat is constant.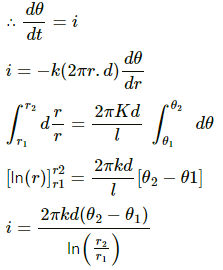
 

Q.21. A hollow tube has a length l, inner radius R₁ and outer radius R₂. The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T₁ and T₂ (T₂ > T₁) (b) the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂.

(a)  When the flat ends are maintained at temperatures T₁ and T₂ (where T₂ > T₁):
Area of cross section through which heat is flowing,

Rate of flow of heat =

(b)

When the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂:
Let us consider a cylindrical shell of radius r and thickness dr.
Rate of flow of heat,

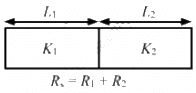
Q.22. A composite slab is prepared by pasting two plates of thickness L₁ and L₂ and thermal conductivites K₁ and K₂. The slabs have equal cross-sectional area. Find the equivalent conductivity of the composite slab.

It is equivalent to the series combination of 2 resistors.
? R_S = R₁ +R₂
Resistance of a conducting slab,

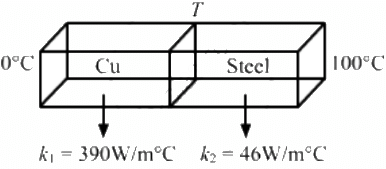
Q.23. Figure (28-E2) shows a copper rod joined to a steel rod. The rods have equal length and equal cross sectional area. The free end of the copper rod is kept at 0°C and that of the steel rod is kept at 100°C. Find the temperature at the junction of the rods. Conductivity of copper = 390 W m^?1°C^?1 and that if steel = 46 W m^?1°C^?1.

Rods are connected in series, so the rate of flow of heat is same.

Rate of flow of heat is given by

? 390 T = (100 - T) 46
? T = 10.6° C

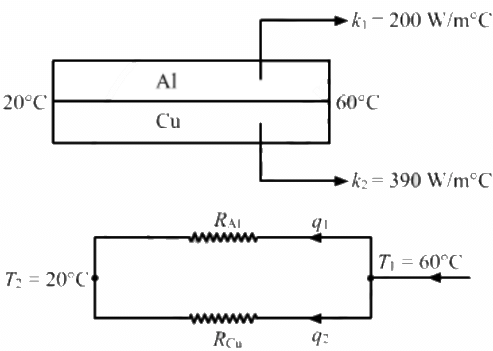
Q.24. An aluminium rod and a copper rod of equal length 1.0 m and cross-sectional area 1 cm² are welded together as shown in the figure . One end is kept at a temperature of 20°C and the other at 60°C. Calculate the amount of heat taken out per second from the hot end. Thermal conductivity of aluminium = 200 W m^?1°C^?1 and of copper = 390 W m^?1°C^?1.

q₁ and q₂ are heat currents. In other words, they are the rates of flow of heat through aluminium and copper rod, respectively.
Applying KVL at the hot junction, we get
q = q₁ + q₂
Rate of heat flow,
As q = q₁ + q₂

Kp =K₁ + k₂
= 390 + 200 = 590 W/m°C

q= 2.36 W

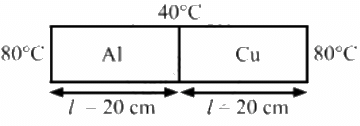
Q.25. Following Figure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20 cm and area of cross section 0.20 cm². The junction is maintained at a constant temperature 40°C and the two ends are maintained at 80°C. Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivites are K_At = 200 W m^?1°C^?1 and K_Cu = 400 W m^?1°C^?1.

Area of cross section, A = 0.20 cm² = 0.2 × 10^–4 m²
Thermal conductivity of aluminium, K_Al = 200 W/m °C
Thermal conductivity of copper, K_Cu = 400 W/m°C
Total heat flowing per second = q_Al + q_Cu

Heat drawn in 1 minute = 2.4 × 60 = 144 J.